入职第二周,上了三天班又放假啦 回溯套路
回溯算法的模板:
不合适就退回上一步
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
子集问题:要用 start 参数排除已选择的数字
组合问题利用的是回溯思想,结果可以表示成树结构,我们只要套用回溯算法模板即可,关键点在于要用一个 start 排除已经选择过的数字。更新 res 的地方是树的底端,k 限制了树的高度,n 限制了树的宽度
77. 组合

回溯法:遍历从first到n的所有整数,将i添加到cur中,继续向组合中添加更多的数,直到当cur的长度满足要求时,添加到结果中
然后将i从cur中移除,实现回溯

class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
res=[]
def helper(first,cur):
if len(cur)==k:
res.append(cur[:])
for i in range(first,n+1):
cur.append(i)
helper(i+1,cur)
cur.pop()
helper(1,[])
return res
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
res=[]
n=len(nums)
def helper(nums,start,cur):
res.append(cur[:])
for i in range(start,n):
cur.append(nums[i])
helper(nums,i+1,cur)
cur.pop()
helper(nums,0,[])
return res
class Solution:
def letterCasePermutation(self, S: str) -> List[str]:
res=[]
def helper(S,start,cur):
if len(cur)==len(S):
res.append(cur)
return
for i in range(start,len(S)):
if S[i].isalpha():
helper(S,i+1,cur+S[i].lower())
helper(S,i+1,cur+S[i].upper())
else:
helper(S,i+1,cur+S[i])
helper(S,0,'')
return res
90. 子集 II

考虑重复的一定要排序
同一递归层级不应该出现同样的元素,如果遇到不是首元素且当前元素和之前元素相同,则剪枝
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
res=[]
nums.sort()
def helper(nums,start,cur):
res.append(cur[:])
for i in range(start,len(nums)):
if i>start and nums[i]==nums[i-1]:#剪枝
continue
cur.append(nums[i])
helper(nums,i+1,cur)
cur.pop()
helper(nums,0,[])
return res
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
res=[]
candidates.sort()
n=len(candidates)
def helper(start,target,cur,n):
if target==0:
res.append(cur[:])
return
for i in range(start,n):
#当前值大于剩余的目标值,剪枝,后面分支也不需要执行
num=target-candidates[i]
if num<0:
break
cur.append(candidates[i])
#可以存在重复数字,且下一层不能比上一层还小
helper(i,num,cur,n)
cur.pop()
helper(0,target,[],n)
return res
40. 组合总和 II

第 39 题:candidates 中的数字可以无限制重复被选取。
第 40 题:candidates 中的每个数字在每个组合中只能使用一次。
编码的不同在于下一层递归的起始索引不一样。
第 39 题:还从候选数组的当前索引值开始。
第 40 题:从候选数组的当前索引值的下一位开始。
解集不能包含重复的组合:
为了使得解集不包含重复的组合。我们想一想,如何去掉一个数组中重复的元素,除了使用哈希表以外,我们还可以先对数组升序排序,重复的元素一定不是排好序以后的第 1 个元素和相同元素的第 1 个元素。根据这个思想,我们先对数组升序排序是有必要的。候选数组有序,对于在递归树中发现重复分支,进而“剪枝”也是有效的。
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
res=[]
candidates.sort()
def helper(start,target,cur):
if target==0:
res.append(cur[:])
return
for i in range(start,len(candidates)):
if candidates[i]>target:
break
if i>start and candidates[i]==candidates[i-1]:
continue
num=target-candidates[i]
cur.append(candidates[i])
helper(i+1,num,cur)
cur.pop()
helper(0,target,[])
return res
class Solution:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
res=[]
def helper(start,target,cur):
if len(cur)==k and target==0:
res.append(cur[:])
return
for i in range(start,10):
if i>target:
break
cur.append(i)
num=target-i
helper(i+1,num,cur)
cur.pop()
helper(1,n,[])
return res
class Solution:
def combinationSum4(self, nums: List[int], target: int) -> int:
nums.sort()
res=[]
def helper(start,target,cur):
if target==0:
res.append(cur[:])
return
for i in range(start,len(nums)):
if nums[i]>target:
break
num=target-nums[i]
cur.append(nums[i])
helper(start,num,cur)
cur.pop()
helper(0,target,[])
return len(res)
由于不用求出具体解,只需要个数,则可以考虑动态规划
class Solution:
def combinationSum4(self, nums: List[int], target: int) -> int:
if not nums:
return 0
#dp[i]:由nums里面的数组成的和为i的组合个数
dp=[0]*(target+1)
dp[0]=1
for i in range(1,target+1):
for j in range(len(nums)):
if nums[j]<=i:
dp[i]+=dp[i-nums[j]]
return dp[-1]
46 全排列

用 nums[:i] + nums[i+1:] 避开了重复利用的问题
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
res=[]
n=len(nums)
def helper(nums,cur):
if len(cur)==n:
res.append(cur[:])
for i in range(len(nums)):
cur.append(nums[i])
helper(nums[:i]+nums[i+1:],cur)
cur.pop()
helper(nums,[])
return res
47. 全排列 II

重复元素的一定要先排序
用nums[i]==nums[i-1],进行剪枝
class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
res=[]
nums.sort()
n=len(nums)
def helper(nums,cur):
if len(cur)==n:
res.append(cur[:])
for i in range(len(nums)):
#nums[i]==nums[i-1]:实现剪枝
if i>0 and nums[i]==nums[i-1]:
continue
cur.append(nums[i])
#nums[:i]+nums[i+1:]:避免选取重复,#每当进入新的构成,先考虑该构成的首字符是否和上一个一样。
helper(nums[:i]+nums[i+1:],cur)
cur.pop()
helper(nums,[])
return res
1219. 黄金矿工


找到所有的起点
对其上左下右方向进行搜索,直到走不动为止。
class Solution:
def getMaximumGold(self, grid: List[List[int]]) -> int:
self.res=0
m,n=len(grid),len(grid[0])
#标记走过的格子
visited=[[0]*n for i in range(m)]
def helper(x,y,cur):
cur+=grid[x][y]
self.res=max(self.res,cur)
visited[x][y]=1
for i,j in [(0,1),(1,0),(0,-1),(-1,0)]:
if 0<=i+x<m and 0<=j+y<n and visited[i+x][j+y]!=1 and grid[i+x][j+y]!=0:
helper(i+x,j+y,cur)
#回溯,相当于把金子放回去
visited[x][y]=0
#任何一个位置都是起点
for i in range(m):
for j in range(n):
if grid[i][j]!=0:
helper(i,j,0)
return self.res
89. 格雷编码



从空字符串开始,上面的(绿色)分别加0、1,下面的(红色)分别加1、0,直到长度达n
class Solution:
def grayCode(self, n: int) -> List[int]:
if n==0:
return [0]
res=[]
def helper(x,cur):
if len(cur)==n:
res.append(int(cur,2))
elif x=='0':
helper('0',cur+'0')
helper('1',cur+'1')
else:
helper('0',cur+'1')
helper('1',cur+'0')
helper('0','')
return res
717. 1比特与2比特字符

线性扫描:当bit[i]为1时,说明是两比特字符,如果bits[i]=0,那么说明这是一个一比特字符,将 i 的值增加 1。如果 i最终落在了 bits.length−1 的位置,那么说明最后一位一定是一比特字符。
class Solution:
def isOneBitCharacter(self, bits: List[int]) -> bool:
i=0
n=len(bits)
while i<n-1:
if bits[i]==1:
i+=2
else:
i+=1
return i==n-1
1079. 活字印刷
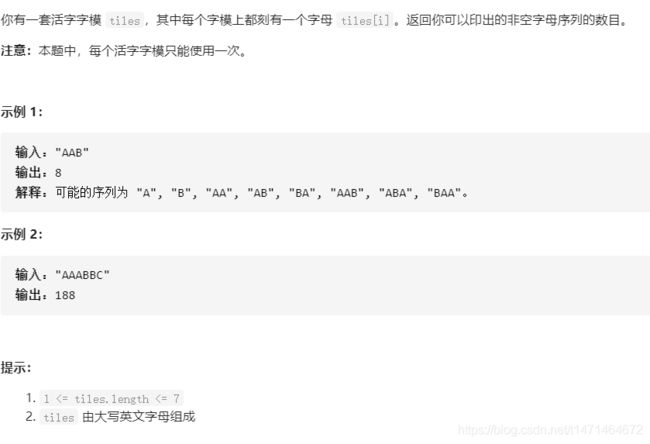
回溯法,与求子集一样,只是要去掉空子集
class Solution:
def numTilePossibilities(self, tiles: str) -> int:
self.res=0
nums=sorted(tiles)
def helper(nums,cur):
#把空集去掉
if cur:
self.res+=1
for i in range(len(nums)):
if i>0 and nums[i]==nums[i-1]:
continue
helper(nums[:i]+nums[i+1:],cur+[nums[i]])
helper(nums,[])
return self.res
# def helper(nums):
# self.res+=1
# for i in range(len(nums)):
# if i>0 and nums[i]==nums[i-1]:
# continue
# helper(nums[:i]+nums[i+1:])
# helper(nums)
# return self.res-1
class Solution:
def permutation(self, s: str) -> List[str]:
nums=sorted(s)
res=[]
def helper(nums,cur):
if not nums:
res.append(cur)
for i in range(len(nums)):
if i>0 and nums[i]==nums[i-1]:
continue
helper(nums[:i]+nums[i+1:],cur+nums[i])
helper(nums,'')
return res
面试题 08.07. 无重复字符串的排列组合

上一题的简单版
class Solution:
def permutation(self, S: str) -> List[str]:
res=[]
def helper(nums,cur):
if not nums:
res.append(cur)
for i in range(len(nums)):
helper(nums[:i]+nums[i+1:],cur+nums[i])
helper(S,'')
return res
class Solution:
def sequentialDigits(self, low: int, high: int) -> List[int]:
res=[]
def helper(num):
if low<=num<=high:
res.append(num)
tmp=num%10
if tmp!=9:
num=num*10+tmp+1
helper(num)
#起始数字要考虑到每一位
for i in range(1,10):
helper(i)
return sorted(res)
class Solution:
def partition(self, s: str) -> List[List[str]]:
res=[]
def helper(nums,cur):
if not nums:
res.append(cur[:])
for i in range(1,len(nums)+1):
if nums[:i]==nums[:i][::-1]:
cur.append(nums[:i])
helper(nums[i:],cur)
cur.pop()
helper(s,[])
return res







