最优化方法(学习笔记)-第三章凸函数
凸函数
- 基本性质
- 凸函数
- 凸函数限制到直线(降维)
- 凸函数f的延拓extended-value extension
- Sublevel set
- Epigraph
- Jensen不等式
- 小结(判定凸函数的5种方法)
- 保凸运算
- 非负权和nonegative weight sum
- 仿射函数复合composition with affine function
- 逐点最大Pointwise maximum
- 逐点上界Pointwise supremum
- 标量函数的耦合Composition with scalar functions
- 向量的耦合Vector composition
- 最小值Minimization
- 舒尔补Schur complement-n×n方阵分块
- 透射函数Perspective
- 小结
- 共轭函数Conjugate function
- 次凸函数Quasiconvex|次凹函数Quasiconcave
- 取log意义下的凹函数log-concave和凸函数log-convex
- 广义不等关系的凸性
- 总结
基本性质
凸函数
定义:
f : R n → R f:R^n\rightarrow R f:Rn→R是凸性的,需要符合以下条件
- d o m f domf domf是凸性的
- ∀ x , y ∈ d o m f , ∀ θ ∈ [ 0 , 1 ] , f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) \forall x,y\isin domf,\forall \theta\isin[0,1],f(\theta x+(1-\theta)y)\leq\theta f(x)+(1-\theta)f(y) ∀x,y∈domf,∀θ∈[0,1],f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)
- 不等式没有等号的时候,就是严格凸函数

性质:
f f f是凸函数,那么 − f -f −f是凹函数
例子: x ∈ R x\isin R x∈R
- 凸函数
- 仿射函数: a x + b , x ∈ R , ∀ a , b ∈ R ax+b,x\isin R,\forall a,b\isin R ax+b,x∈R,∀a,b∈R
- 指数函数: e a x , ∀ a ∈ R e^{ax},\forall a\isin R eax,∀a∈R
- 幂函数: x a , x ∈ R + + , ∀ a ∈ [ − ∞ , 0 ] ∪ [ 1 , + ∞ ] x^{a},x\isin R_{++},\forall a\isin[-\infty,0]\cup[1,+\infty] xa,x∈R++,∀a∈[−∞,0]∪[1,+∞]
- P函数: ∣ x ∣ p , x ∈ R + + , ∀ p ∈ [ 1 , + ∞ ] |x|^{p},x\isin R_{++},\forall p\isin[1,+\infty] ∣x∣p,x∈R++,∀p∈[1,+∞](幂函数带绝对值-偶函数)
- 负熵函数: x log x , x ∈ R + + x\log{x},x\isin R_{++} xlogx,x∈R++
- 凹函数
- 仿射函数: a x + b , x ∈ R , ∀ a , b ∈ R ax+b,x\isin R,\forall a,b\isin R ax+b,x∈R,∀a,b∈R
- 幂函数: x a , x ∈ R , ∀ a ∈ [ 1 , + ∞ ] x^{a},x\isin R,\forall a\isin[1,+\infty] xa,x∈R,∀a∈[1,+∞]
- log函数: log x , x ∈ R + + \log{x},x\isin R_{++} logx,x∈R++
例子: x ∈ R n x\isin R^n x∈Rn
- 仿射函数(可凸可凹): f ( x ) = a T x + b f(x)=a^Tx+b f(x)=aTx+b
- 范数: ∣ ∣ x ∣ ∣ p = ( ∑ i = 1 n ∣ x i ∣ p ) 1 p , p ∈ [ 1 , + ∞ ] , ∣ ∣ x ∣ ∣ ∞ = m a x k ∣ x k ∣ ||x||_p=(\sum_{i=1}^n|x_i|^p)^{\frac{1}{p}},p\isin[1,+\infty],||x||_\infty=max_k|x_k| ∣∣x∣∣p=(∑i=1n∣xi∣p)p1,p∈[1,+∞],∣∣x∣∣∞=maxk∣xk∣
例子: x ∈ R m × n x\isin R^{m\times n} x∈Rm×n
- 仿射函数(可凸可凹): f ( X ) = t r ( a T X ) + b = ∑ i = 1 m ∑ j = 1 n A i j X i j + b f(X)=tr(a^TX)+b=\sum\limits_{i=1}^m\sum\limits_{j=1}^nA_{ij}X_{ij}+b f(X)=tr(aTX)+b=i=1∑mj=1∑nAijXij+b
- 最大奇异值范数spectral norm: f ( X ) = ∣ ∣ X ∣ ∣ 2 = σ m a x ( X ) = ( λ m a x ( X T X ) ) 1 2 f(X)=||X||_2=\sigma_{max}(X)=(\lambda_{max}(X^TX))^{\frac{1}{2}} f(X)=∣∣X∣∣2=σmax(X)=(λmax(XTX))21
凸函数限制到直线(降维)
f : R n → R f:R^n\rightarrow R f:Rn→R有凸性 ⟺ 凸 函 数 g : R → R ( g ( t ) = f ( x + t v ) ) , d o m g = { t ∣ x + t v ∈ d o m f } , t ∈ R , x ∈ d o m f , x 是 原 点 , v ∈ R n , v 是 方 向 \iff 凸函数g:R\rightarrow R(g(t)=f(x+tv)),domg=\{t|x+tv\isin domf\},t\isin R,x\isin domf,x是原点,v\isin R^n,v是方向 ⟺凸函数g:R→R(g(t)=f(x+tv)),domg={t∣x+tv∈domf},t∈R,x∈domf,x是原点,v∈Rn,v是方向
也就是:高维凸函数 ⟺ \iff ⟺高维函数的每个维度上都是凸函数
凸函数f的延拓extended-value extension
{ f ~ = f ( x ) , ∀ x ∈ d o m f f ~ = ∞ , x ∉ d o m f \begin{cases}\tilde{f}=f(x),\forall x\isin domf \\ \tilde{f}=\infty,x\notin domf \end{cases} {f~=f(x),∀x∈domff~=∞,x∈/domf
- 凸性定义法
保持凸性——凸性的不等关系性质成立
f ( θ x + ( 1 − θ ) y ) ~ ≤ θ f ( x ) ~ + ( 1 − θ ) f ( y ) ~ \widetilde{f(\theta x+(1-\theta)y)}\leq\theta\widetilde{f(x)}+(1-\theta)\widetilde{f(y)} f(θx+(1−θ)y) ≤θf(x) +(1−θ)f(y)
其中: { x ∣ f ( x ) ~ < ∞ } ⟺ x ∈ d o m f \{x|\widetilde{f(x)}<\infty\}\iff x\isin domf {x∣f(x) <∞}⟺x∈domf - 函数性质判定凸性法
- 一阶条件(first-order condition): f ( x ) 一 阶 可 微 ( d i f f e r e n t i a b l e ) , 定 义 域 ∀ x , y ∈ d o m f ( o p e n ) , 存 在 梯 度 ( 列 向 量 ) 是 ▽ f ( x ) = ( ∂ f ( x ) ∂ x 1 , ∂ f ( x ) ∂ x 2 , . . . , ∂ f ( x ) ∂ x n ) T 【 + 】 f ( y ) ≥ f ( x ) + ▽ f ( x ) T ( y − x ) ⟺ f 有 凸 性 f(x)一阶可微(differentiable),定义域\forall x,y\isin domf(open),存在梯度(列向量)是\triangledown{f(x)}=(\frac{\partial{f(x)}}{\partial{x_1}},\frac{\partial{f(x)}}{\partial{x_2}},...,\frac{\partial{f(x)}}{\partial{x_n}})^T【+】f(y)\geq f(x)+\triangledown{f(x)^T}(y-x) \iff f有凸性 f(x)一阶可微(differentiable),定义域∀x,y∈domf(open),存在梯度(列向量)是▽f(x)=(∂x1∂f(x),∂x2∂f(x),...,∂xn∂f(x))T【+】f(y)≥f(x)+▽f(x)T(y−x)⟺f有凸性
证明:
∗ 1. n = 1 , 即 f ( y ) ≥ f ( x ) + f ′ ( x ) ( y − x ) *1.n=1,即f(y)\geq f(x)+f'(x)(y-x) ∗1.n=1,即f(y)≥f(x)+f′(x)(y−x)
⟵ \longleftarrow ⟵(Assume:f is convex)
给定条件: f ( x + t ( y − x ) ) ≤ ( 1 − t ) f ( x ) + t f ( y ) f(x+t(y-x))\leq(1-t)f(x)+tf(y) f(x+t(y−x))≤(1−t)f(x)+tf(y)
目标: f ( y ) ≥ f ( x ) + f ′ ( x ) ( y − x ) f(y)\geq f(x)+f'(x)(y-x) f(y)≥f(x)+f′(x)(y−x)
过程: f ( y ) ≥ f ( x + t ( y − x ) ) − ( 1 − t ) f ( x ) t = f ( x + t ( y − x ) ) − f ( x ) t + f ( x ) = f ( x ) + f ( x + t ( y − x ) ) − f ( x ) t ( y − x ) ( y − x ) = t → 0 f ( x ) + f ′ ( x ) ( y − x ) f(y)\geq\frac{f(x+t(y-x))-(1-t)f(x)}{t}=\frac{f(x+t(y-x))-f(x)}{t}+f(x)=f(x)+\frac{f(x+t(y-x))-f(x)}{t(y-x)}(y-x)\xlongequal{t\rightarrow 0}f(x)+f'(x)(y-x) f(y)≥tf(x+t(y−x))−(1−t)f(x)=tf(x+t(y−x))−f(x)+f(x)=f(x)+t(y−x)f(x+t(y−x))−f(x)(y−x)t→0f(x)+f′(x)(y−x)
⟶ \longrightarrow ⟶(Assume:不等式成立)
给定条件: f ( y ) ≥ f ( x ) + f ′ ( x ) ( y − x ) f(y)\geq f(x)+f'(x)(y-x) f(y)≥f(x)+f′(x)(y−x)
目标: f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) f(\theta x+(1-\theta)y)\leq\theta f(x)+(1-\theta)f(y) f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)
过程:利用中间点 z = θ x + ( 1 − θ ) y z=\theta x+(1-\theta)y z=θx+(1−θ)y,存在 f ( y ) ≥ f ( z ) + f ′ ( z ) ( y − z ) , f ( x ) ≥ f ( z ) + f ′ ( z ) ( x − z ) f(y)\geq f(z)+f'(z)(y-z),f(x)\geq f(z)+f'(z)(x-z) f(y)≥f(z)+f′(z)(y−z),f(x)≥f(z)+f′(z)(x−z)
f ( y ) 同 乘 ( 1 − θ ) , ( 1 − θ ) f ( y ) ≥ ( 1 − θ ) [ f ( z ) + f ′ ( z ) ( y − z ) ] f(y)同乘(1-\theta),(1-\theta)f(y)\geq (1-\theta)[f(z)+f'(z)(y-z)] f(y)同乘(1−θ),(1−θ)f(y)≥(1−θ)[f(z)+f′(z)(y−z)]
f ( x ) 同 乘 θ , θ f ( x ) ≥ θ [ f ( z ) + f ′ ( z ) ( x − z ) ] f(x)同乘\theta,\theta f(x)\geq \theta [f(z)+f'(z)(x-z)] f(x)同乘θ,θf(x)≥θ[f(z)+f′(z)(x−z)]
两 式 相 加 , ( 1 − θ ) f ( y ) + θ f ( x ) ≥ f ( z ) 两式相加,(1-\theta)f(y)+\theta f(x)\geq f(z) 两式相加,(1−θ)f(y)+θf(x)≥f(z)
∗ 2. n > 1 , x ∈ R n *2.n>1,x\isin R^n ∗2.n>1,x∈Rn
设 g ( t ) = f ( t y + ( 1 − t ) x ) , 所 以 g ′ ( t ) = ▽ f ( t y + ( 1 − t ) x ) T ( y − x ) g(t)=f(ty+(1-t)x),所以g'(t)=\triangledown f(ty+(1-t)x)^T(y-x) g(t)=f(ty+(1−t)x),所以g′(t)=▽f(ty+(1−t)x)T(y−x)
⟵ \longleftarrow ⟵(Assume:f is convex,then g is convex)
给定条件: g ( t ) 凸 性 定 义 : g ( t ) ≥ g ( τ ) + g ′ ( τ ) ( t − τ ) [ 一 维 的 时 候 ] g(t)凸性定义:g(t)\geq g(\tau)+g'(\tau)(t-\tau)[一维的时候] g(t)凸性定义:g(t)≥g(τ)+g′(τ)(t−τ)[一维的时候]
目标: f ( y ) ≥ f ( x ) + ▽ f ( x ) T ( y − x ) f(y)\geq f(x)+\triangledown f(x)^T(y-x) f(y)≥f(x)+▽f(x)T(y−x)
过程: 若 t = 1 , τ = 0 , 有 g ( 1 ) ≥ g ( 0 ) + g ′ ( 0 ) ( 1 − 0 ) 若t=1,\tau=0,有g(1)\geq g(0)+g'(0)(1-0) 若t=1,τ=0,有g(1)≥g(0)+g′(0)(1−0)
将 值 带 回 f 函 数 有 f ( y ) ≥ f ( x ) + ▽ f ( x ) T ( y − x ) 将值带回f函数有f(y)\geq f(x)+\triangledown f(x)^T(y-x) 将值带回f函数有f(y)≥f(x)+▽f(x)T(y−x),不等式成立
⟶ \longrightarrow ⟶(Assume:不等式成立)
给定条件: f ( y ) ≥ f ( x ) + ▽ f ( x ) T ( y − x ) f(y)\geq f(x)+\triangledown f(x)^T(y-x) f(y)≥f(x)+▽f(x)T(y−x)
目标: ∀ t , τ ∈ R , g ( t ) ≥ g ( τ ) + g ′ ( τ ) ( t − τ ) [ g 函 数 有 凸 性 ] ⟺ f ( t y + ( 1 − t ) x ) ≥ f ( τ y + ( 1 − τ ) x ) + ▽ f ( τ y + ( 1 − τ ) x ) T ( y − x ) ( t − τ ) \forall t,\tau\isin R,g(t)\geq g(\tau)+g'(\tau)(t-\tau)[g函数有凸性]\iff f(ty+(1-t)x)\geq f(\tau y+(1-\tau)x)+\triangledown{f(\tau y+(1-\tau)x)^T}(y-x)(t-\tau) ∀t,τ∈R,g(t)≥g(τ)+g′(τ)(t−τ)[g函数有凸性]⟺f(ty+(1−t)x)≥f(τy+(1−τ)x)+▽f(τy+(1−τ)x)T(y−x)(t−τ)
过程:令 Y = t y + ( 1 − t ) x , X = τ y + ( 1 − τ ) x , B = Y − X Y=ty+(1-t)x,X=\tau y+(1-\tau)x,B=Y-X Y=ty+(1−t)x,X=τy+(1−τ)x,B=Y−X
所以 f ( t y + ( 1 − t ) x ) ≥ f ( τ y + ( 1 − τ ) x ) + ▽ f ( τ y + ( 1 − τ ) x ) T ∗ B f(ty+(1-t)x)\geq f(\tau y+(1-\tau)x)+\triangledown{f(\tau y+(1-\tau)x)^T}*B f(ty+(1−t)x)≥f(τy+(1−τ)x)+▽f(τy+(1−τ)x)T∗B
B = Y − X = t y + ( 1 − t ) x − [ τ y + ( 1 − τ ) x ] = t y + x − t x − τ y − x + τ x = t ( y − x ) − τ ( y − x ) = ( y − x ) ( t − τ ) B=Y-X=ty+(1-t)x-[\tau y+(1-\tau)x]=ty+x-tx-\tau y-x+\tau x=t(y-x)-\tau(y-x)=(y-x)(t-\tau) B=Y−X=ty+(1−t)x−[τy+(1−τ)x]=ty+x−tx−τy−x+τx=t(y−x)−τ(y−x)=(y−x)(t−τ),凸性成立 - 二阶条件(second-order condition): f ( x ) 二 阶 可 微 ( t w i c e d i f f e r e n t i a b l e ) , 定 义 域 ∀ x ∈ d o m f ( o p e n ) , 存 在 二 阶 导 数 ( 矩 阵 ) ▽ 2 f ( x ) i j = ∂ 2 f ( x ) ∂ x i ∂ x j , i , j = 1 , . . . , n 【 + 】 定 义 域 d o m f 是 凸 的 , 二 阶 导 数 是 正 定 ▽ 2 f ( x ) ≥ 0 ⟺ f 有 凸 性 ( ≥ 0 ) f(x)二阶可微(twice\space differentiable),定义域\forall x\isin domf(open),存在二阶导数(矩阵)\triangledown^2{f(x)_{ij}}=\frac{\partial^2{f(x)}}{\partial{x_i}\partial{x_j}},i,j=1,...,n【+】定义域domf是凸的,二阶导数是正定\triangledown^2{f(x)}\geq 0 \iff f有凸性(\geq 0) f(x)二阶可微(twice differentiable),定义域∀x∈domf(open),存在二阶导数(矩阵)▽2f(x)ij=∂xi∂xj∂2f(x),i,j=1,...,n【+】定义域domf是凸的,二阶导数是正定▽2f(x)≥0⟺f有凸性(≥0)
例子:- 二次函数quadratic function: f ( x ) = 1 2 x T P x + q T x + r , P ∈ S n f(x)=\frac{1}{2}x^TPx+q^Tx+r,P\isin S^n f(x)=21xTPx+qTx+r,P∈Sn,二阶导系数矩阵 ▽ 2 f ( x ) = P \triangledown^2{f(x)}=P ▽2f(x)=P是对称矩阵(特征值是实数),再要求 P ≥ 0 P\geq 0 P≥0(特征值大于等于0)
- 最小二乘目标least-squares objective: f ( x ) = ∣ ∣ A x − b ∣ ∣ 2 2 , ▽ f ( x ) = 2 A T ( A x − b ) , ▽ 2 f ( x ) = 2 A T A f(x)=||Ax-b||_2^2,\triangledown{f(x)}=2A^T(Ax-b),\triangledown^2{f(x)}=2A^TA f(x)=∣∣Ax−b∣∣22,▽f(x)=2AT(Ax−b),▽2f(x)=2ATA(特征值一定大于等于0)
- 二次线性quadratic-over-linear: f ( x , y ) = x 2 y , y > 0 , ▽ 2 f ( x , y ) = [ ∂ 2 f ( x , y ) ∂ x 2 ∂ 2 f ( x , y ) ∂ x ∂ y ∂ 2 f ( x , y ) ∂ y ∂ x ∂ 2 f ( x , y ) ∂ y 2 ] = [ 2 y − 2 x y 2 − 2 x y 2 2 x 2 y 3 ] = 2 y 3 [ y 2 − x y − x y x 2 ] = 2 y 3 [ y − x ] [ y − x ] T ≥ 0 f(x,y)=\frac{x^2}{y},y>0,\triangledown^2{f(x,y)}=\begin{bmatrix}\frac{\partial^2{f(x,y)}}{\partial{x}^2} & \frac{\partial^2{f(x,y)}}{\partial{x}\partial{y}} \\ \frac{\partial^2{f(x,y)}}{\partial{y}\partial{x}} & \frac{\partial^2{f(x,y)}}{\partial{y}^2} \end{bmatrix}=\begin{bmatrix}\frac{2}{y} & -\frac{2x}{y^2} \\ -\frac{2x}{y^2} & \frac{2x^2}{y^3} \end{bmatrix}=\frac{2}{y^3}\begin{bmatrix}y^2 & -xy \\ -xy & x^2 \end{bmatrix}=\frac{2}{y^3}\begin{bmatrix}y \\ -x \end{bmatrix}{\begin{bmatrix}y \\ -x \end{bmatrix}}^T\geq 0 f(x,y)=yx2,y>0,▽2f(x,y)=[∂x2∂2f(x,y)∂y∂x∂2f(x,y)∂x∂y∂2f(x,y)∂y2∂2f(x,y)]=[y2−y22x−y22xy32x2]=y32[y2−xy−xyx2]=y32[y−x][y−x]T≥0
- 对数的偏分函数(softmax): f ( x ) = − log ∑ k = 1 n exp x k , 设 z k = e x k = exp x k , ▽ 2 f ( x ) = 1 1 T z d i a g ( z ) − 1 ( 1 T z ) 2 z z T f(x)=-\log\sum\limits_{k=1}^n \exp x_k,设z_k=e^{x_k}=\exp x_k,\triangledown^2{f(x)}=\frac{1}{1^Tz}diag(z)-\frac{1}{(1^Tz)^2}zz^T f(x)=−logk=1∑nexpxk,设zk=exk=expxk,▽2f(x)=1Tz1diag(z)−(1Tz)21zzT
- 一阶条件(first-order condition): f ( x ) 一 阶 可 微 ( d i f f e r e n t i a b l e ) , 定 义 域 ∀ x , y ∈ d o m f ( o p e n ) , 存 在 梯 度 ( 列 向 量 ) 是 ▽ f ( x ) = ( ∂ f ( x ) ∂ x 1 , ∂ f ( x ) ∂ x 2 , . . . , ∂ f ( x ) ∂ x n ) T 【 + 】 f ( y ) ≥ f ( x ) + ▽ f ( x ) T ( y − x ) ⟺ f 有 凸 性 f(x)一阶可微(differentiable),定义域\forall x,y\isin domf(open),存在梯度(列向量)是\triangledown{f(x)}=(\frac{\partial{f(x)}}{\partial{x_1}},\frac{\partial{f(x)}}{\partial{x_2}},...,\frac{\partial{f(x)}}{\partial{x_n}})^T【+】f(y)\geq f(x)+\triangledown{f(x)^T}(y-x) \iff f有凸性 f(x)一阶可微(differentiable),定义域∀x,y∈domf(open),存在梯度(列向量)是▽f(x)=(∂x1∂f(x),∂x2∂f(x),...,∂xn∂f(x))T【+】f(y)≥f(x)+▽f(x)T(y−x)⟺f有凸性
Sublevel set
定义: α − s u b l e v e l s e t o f f : R n → R , C α = { x ∈ d o m f ∣ f ( x ) ≤ α } \alpha-sublevel\space set\space of\space f:R^n\rightarrow R,C_{\alpha}=\{x\isin domf| f(x)\leq \alpha\} α−sublevel set of f:Rn→R,Cα={x∈domf∣f(x)≤α}(要求区间是连续的)
凸函数的Sublevel set是凸性的(其逆函数不一定)

Epigraph
定义: e p i o f f : R n → R , e p i f = { ( x , t ) ∈ R n + 1 ∣ x ∈ d o m f , f ( x ) ≤ t } epi\space of\space f:R^n\rightarrow R,epi\space f=\{(x,t)\isin R^{n+1}| x\isin domf,f(x)\leq t\} epi of f:Rn→R,epi f={(x,t)∈Rn+1∣x∈domf,f(x)≤t}(要求区间是连续的)
f 是 凸 函 数 ⟺ e p i f 是 凸 集 f是凸函数\iff epi\space f是凸集 f是凸函数⟺epi f是凸集
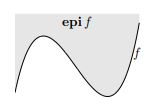
例子(epigraph与一阶导数的关系):
一维情况:已知 x 2 x^2 x2函数的切线(类似支撑面),切点, e p i f epi f epif集合
切线的法向量: ( ▽ f ( x ) , − 1 ) (\triangledown{f(x)},-1) (▽f(x),−1)
tan θ = d f d x ∣ x = x = ▽ f ( x ) 1 \tan{\theta}=\frac{df}{dx}|_{x=x}=\frac{\triangledown{f(x)}}{1} tanθ=dxdf∣x=x=1▽f(x)

若有点 ( y , t ) , 存 在 t ≥ f ( y ) ≥ f ( x ) + ▽ f ( x ) T ( y − x ) (y,t),存在t\geq f(y)\geq f(x)+\triangledown{f(x)}^T(y-x) (y,t),存在t≥f(y)≥f(x)+▽f(x)T(y−x)
前一个不等式是因为epigraph,后一个不等式是因为一阶导数的性质
所以推导: − ( t − f ( x ) ) + ▽ f ( x ) T ( y − x ) ≤ 0 ⟹ [ ▽ f ( x ) − 1 ] T [ y − x t − f ( x ) ] ≤ 0 -(t-f(x))+\triangledown{f(x)}^T(y-x)\leq 0\implies \begin{bmatrix}\triangledown{f(x)} \\ -1 \end{bmatrix}^T\begin{bmatrix}y-x \\ t-f(x) \end{bmatrix}\leq 0 −(t−f(x))+▽f(x)T(y−x)≤0⟹[▽f(x)−1]T[y−xt−f(x)]≤0(就是两个蓝色的向量内积是小于0的)
Jensen不等式
定义-基本:
∀ θ ∈ [ 0 , 1 ] , 凸 函 数 f , f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) \forall \theta\isin[0,1],凸函数f,f(\theta x+(1-\theta)y)\leq\theta f(x)+(1-\theta)f(y) ∀θ∈[0,1],凸函数f,f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)
定义-扩展:
f ( ∑ i = 1 n θ i x i ) ≤ ∑ i = 1 n θ i f ( x i ) , ∑ i = 1 n θ i = 1 , θ i ∈ [ 0 , 1 ] f(\sum\limits_{i=1}^n\theta_ix_i)\leq\sum\limits_{i=1}^n\theta_if(x_i),\sum\limits_{i=1}^n\theta_i=1,\theta_i\isin[0,1] f(i=1∑nθixi)≤i=1∑nθif(xi),i=1∑nθi=1,θi∈[0,1]
考 虑 随 机 取 值 的 情 况 : f ( 1 n ∑ i = 1 n x i ) ≤ 1 n ∑ i = 1 n f ( x i ) , 于 是 f ( E X ) ≤ E f ( x ) 考虑随机取值的情况:f(\frac{1}{n}\sum\limits_{i=1}^nx_i)\leq \frac{1}{n}\sum\limits_{i=1}^nf(x_i),于是f(EX)\leq Ef(x) 考虑随机取值的情况:f(n1i=1∑nxi)≤n1i=1∑nf(xi),于是f(EX)≤Ef(x)
小结(判定凸函数的5种方法)
- 定义法:
f : R n → R f:R^n\rightarrow R f:Rn→R是凸函数 ⟺ d o m f \iff domf ⟺domf定义域是凸的, ∀ x , y ∈ d o m f , ∀ θ ∈ [ 0 , 1 ] , f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) \forall x,y\isin domf,\forall \theta\isin[0,1],f(\theta x+(1-\theta)y)\leq\theta f(x)+(1-\theta)f(y) ∀x,y∈domf,∀θ∈[0,1],f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y) - 高维限制法:
f : R n → R f:R^n\rightarrow R f:Rn→R是凸函数 ⟺ 凸 函 数 g : R → R ( g ( t ) = f ( x + t v ) ) , d o m g = { t ∣ x + t v ∈ d o m f } 是 凸 集 , t ∈ R , x ∈ d o m f , x 是 原 点 , v ∈ R n , v 是 方 向 \iff 凸函数g:R\rightarrow R(g(t)=f(x+tv)),dom g=\{t|x+tv\isin domf\}是凸集,t\isin R,x\isin domf,x是原点,v\isin R^n,v是方向 ⟺凸函数g:R→R(g(t)=f(x+tv)),domg={t∣x+tv∈domf}是凸集,t∈R,x∈domf,x是原点,v∈Rn,v是方向 - 一阶条件法:
f ( x ) 一 阶 可 微 ( d i f f e r e n t i a b l e ) , 定 义 域 ∀ x , y ∈ d o m f ( o p e n ) , 定 义 域 d o m f 是 凸 的 , 存 在 梯 度 ( 列 向 量 ) 是 ▽ f ( x ) = ( ∂ f ( x ) ∂ x 1 , ∂ f ( x ) ∂ x 2 , . . . , ∂ f ( x ) ∂ x n ) T , f 是 凸 函 数 ⟺ f ( y ) ≥ f ( x ) + ▽ f ( x ) T ( y − x ) f(x)一阶可微(differentiable),定义域\forall x,y\isin domf(open),定义域domf是凸的,存在梯度(列向量)是\triangledown{f(x)}=(\frac{\partial{f(x)}}{\partial{x_1}},\frac{\partial{f(x)}}{\partial{x_2}},...,\frac{\partial{f(x)}}{\partial{x_n}})^T,f是凸函数\iff f(y)\geq f(x)+\triangledown{f(x)^T}(y-x) f(x)一阶可微(differentiable),定义域∀x,y∈domf(open),定义域domf是凸的,存在梯度(列向量)是▽f(x)=(∂x1∂f(x),∂x2∂f(x),...,∂xn∂f(x))T,f是凸函数⟺f(y)≥f(x)+▽f(x)T(y−x) - 二阶条件法:
f ( x ) 二 阶 可 微 ( t w i c e d i f f e r e n t i a b l e ) , 定 义 域 ∀ x ∈ d o m f ( o p e n ) , 定 义 域 d o m f 是 凸 的 , 存 在 二 阶 导 数 ( 矩 阵 ) ▽ 2 f ( x ) i j = ∂ 2 f ( x ) ∂ x i ∂ x j , i , j = 1 , . . . , n , f 是 凸 函 数 ( ≥ 0 ) ⟺ 二 阶 导 数 是 正 定 ▽ 2 f ( x ) ≥ 0 f(x)二阶可微(twice\space differentiable),定义域\forall x\isin domf(open),定义域domf是凸的,存在二阶导数(矩阵)\triangledown^2{f(x)_{ij}}=\frac{\partial^2{f(x)}}{\partial{x_i}\partial{x_j}},i,j=1,...,n,f是凸函数(\geq 0)\iff 二阶导数是正定\triangledown^2{f(x)}\geq 0 f(x)二阶可微(twice differentiable),定义域∀x∈domf(open),定义域domf是凸的,存在二阶导数(矩阵)▽2f(x)ij=∂xi∂xj∂2f(x),i,j=1,...,n,f是凸函数(≥0)⟺二阶导数是正定▽2f(x)≥0 - epi图法:
f : R n → R f:R^n\rightarrow R f:Rn→R是凸函数 ⟺ e p i o f f : R n → R , e p i f = { ( x , t ) ∈ R n + 1 ∣ x ∈ d o m f , f ( x ) ≤ t } \iff epi\space of\space f:R^n\rightarrow R,epi\space f=\{(x,t)\isin R^{n+1}| x\isin domf,f(x)\leq t\} ⟺epi of f:Rn→R,epi f={(x,t)∈Rn+1∣x∈domf,f(x)≤t}(要求区间是连续的)是凸的
保凸运算
非负权和nonegative weight sum
定义:
逐点求和:
α i ≥ 0 , f i 是 凸 函 数 → f ( x ) = ∑ i = 1 k α i f i 是 凸 函 数 \alpha_i\geq 0,f_i是凸函数\rightarrow f(x)=\sum\limits_{i=1}^k\alpha_if_i是凸函数 αi≥0,fi是凸函数→f(x)=i=1∑kαifi是凸函数(线性变换保凸)
求和转变为积分形式
无穷点求和:
f ( x ) 是 凸 函 数 , ∀ y , w ( y ) ≥ 0 → g ( x ) = ∫ Ω f ( x , y ) w ( y ) d y 是 凸 函 数 f(x)是凸函数,\forall y,w(y)\geq 0\rightarrow g(x)=\int_\Omega f(x,y)w(y)dy是凸函数 f(x)是凸函数,∀y,w(y)≥0→g(x)=∫Ωf(x,y)w(y)dy是凸函数
仿射函数复合composition with affine function
定义:
f ( x ) 是 凸 函 数 → f ( A x + b ) 是 凸 函 数 f(x)是凸函数\rightarrow f(Ax+b)是凸函数 f(x)是凸函数→f(Ax+b)是凸函数
例子:
- log barrier
f ( x ) = − ∑ i = 1 m log ( b i − a i T x ) , d o m f = { x ∣ b i − a i T x > 0 , ∀ i } f(x)=-\sum\limits_{i=1}^m\log{(b_i-a_i^Tx)},dom f=\{x|b_i-a_i^Tx>0,\forall i\} f(x)=−i=1∑mlog(bi−aiTx),domf={x∣bi−aiTx>0,∀i} - norm of affine function
f ( x ) = ∣ ∣ A x + b ∣ ∣ f(x)=||Ax+b|| f(x)=∣∣Ax+b∣∣
逐点最大Pointwise maximum
定义:
f 1 ( x ) , f 2 ( x ) 是 凸 函 数 → f ( x ) = m a x { f 1 ( x ) , f 2 ( x ) } 是 凸 函 数 f_1(x),f_2(x)是凸函数\rightarrow f(x)=max\{f_1(x),f_2(x)\}是凸函数 f1(x),f2(x)是凸函数→f(x)=max{f1(x),f2(x)}是凸函数
例子:
x ∈ R m , X [ 1 ] > X [ 2 ] > . . . > X [ n ] , f ( x ) = max { x i 1 + x i 2 + . . . + x i r ∣ 1 ≤ i 1 < i 2 < . . . < i r ≤ n } 是 凸 函 数 x\isin R^m,X_[1]>X_[2]>...>X_[n],f(x)=\max\{x_{i_1}+x_{i_2}+...+x_{i_r}|1\leq i_1
逐点上界Pointwise supremum
定义:
∀ y ∈ A , f ( x , y ) 对 x 是 凸 函 数 → g ( x ) = sup y ∈ A f ( x , y ) 是 凸 函 数 ( g 是 f 关 于 y 求 极 值 的 函 数 ) \forall y\isin A,f(x,y)对x是凸函数\rightarrow g(x)=\sup\limits_{y\isin A}f(x,y)是凸函数(g是f关于y求极值的函数) ∀y∈A,f(x,y)对x是凸函数→g(x)=y∈Asupf(x,y)是凸函数(g是f关于y求极值的函数)
例子:
- 集合C的support function: x 是 凸 函 数 → S C ( x ) = sup y ∈ C y T x 是 凸 函 数 x是凸函数\rightarrow S_C(x)=\sup\limits_{y\isin C}y^Tx是凸函数 x是凸函数→SC(x)=y∈CsupyTx是凸函数
- 集合C的最远距离: 求 范 数 是 凸 函 数 → f ( x ) = sup y ∈ C ∣ ∣ x − y ∣ ∣ 求范数是凸函数\rightarrow f(x)=\sup\limits_{y\isin C}||x-y|| 求范数是凸函数→f(x)=y∈Csup∣∣x−y∣∣
- 对称矩阵( X ∈ S n X\isin S^n X∈Sn)的最大特征值(eigenvalue): 对 称 矩 阵 X 线 性 仍 是 凸 函 数 → λ m a x ( X ) = sup ∣ ∣ y ∣ ∣ 2 = 1 y T X y 对称矩阵X线性仍是凸函数\rightarrow \lambda_{max}(X)=\sup\limits_{||y||_2=1}y^TXy 对称矩阵X线性仍是凸函数→λmax(X)=∣∣y∣∣2=1supyTXy
标量函数的耦合Composition with scalar functions
定义:
g : R n → R , h : R → R , f ( x ) = h ( g ( x ) ) , f ′ ( x ) = h ′ ( g ( x ) ) g ′ ( x ) , f ′ ′ ( x ) = h ′ ′ ( g ( x ) ) ( g ′ ( x ) ) 2 + h ′ ( g ( x ) ) g ′ ′ ( x ) g:R^n\rightarrow R,h:R\rightarrow R,f(x)=h(g(x)),f'(x)=h'(g(x))g'(x),f''(x)=h''(g(x))(g'(x))^2+h'(g(x))g''(x) g:Rn→R,h:R→R,f(x)=h(g(x)),f′(x)=h′(g(x))g′(x),f′′(x)=h′′(g(x))(g′(x))2+h′(g(x))g′′(x)
[ 1 ] . g 是 凸 函 数 ( g ′ ′ ≥ 0 ) , h 的 延 拓 h ~ 是 非 递 减 的 ( h ′ ≥ 0 ) , h 是 凸 函 数 ( f ′ ′ ≥ 0 ) [1].g是凸函数(g''\geq 0),h的延拓\tilde{h}是非递减的(h'\geq 0),h是凸函数(f''\geq 0) [1].g是凸函数(g′′≥0),h的延拓h~是非递减的(h′≥0),h是凸函数(f′′≥0)
[ 2 ] . g 是 凹 函 数 ( g ′ ′ ≤ 0 ) , h 的 延 拓 h ~ 是 非 递 增 的 ( h ′ ≤ 0 ) , h 是 凸 函 数 ( f ′ ′ ≥ 0 ) [2].g是凹函数(g''\leq 0),h的延拓\tilde{h}是非递增的(h'\leq 0),h是凸函数(f''\geq 0) [2].g是凹函数(g′′≤0),h的延拓h~是非递增的(h′≤0),h是凸函数(f′′≥0)
→ f ( x ) 是 凸 函 数 ( f ′ ′ ( x ) ≥ 0 ) \rightarrow f(x)是凸函数(f''(x)\geq 0) →f(x)是凸函数(f′′(x)≥0)
证明:
x , y ∈ d o m g , f ( x ) = h ( g ( x ) ) , 证 明 条 件 [ 1 ] 成 立 x,y\isin domg,f(x)=h(g(x)),证明条件[1]成立 x,y∈domg,f(x)=h(g(x)),证明条件[1]成立
1. g 是 凸 函 数 , 所 以 g ( θ x + ( 1 − θ ) y ) ≤ θ g ( x ) + ( 1 − θ ) g ( y ) 1.g是凸函数,所以g(\theta x+(1-\theta)y)\leq \theta g(x)+(1-\theta)g(y) 1.g是凸函数,所以g(θx+(1−θ)y)≤θg(x)+(1−θ)g(y)
2. h 是 凸 函 数 , 所 以 h ( g ( θ x + ( 1 − θ ) y ) ) ≤ h ( θ g ( x ) + ( 1 − θ ) g ( y ) ) ≤ θ h ( g ( x ) ) + ( 1 − θ ) h ( g ( y ) ) 2.h是凸函数,所以h(g(\theta x+(1-\theta)y))\leq h(\theta g(x)+(1-\theta)g(y))\leq \theta h(g(x))+(1-\theta)h(g(y)) 2.h是凸函数,所以h(g(θx+(1−θ)y))≤h(θg(x)+(1−θ)g(y))≤θh(g(x))+(1−θ)h(g(y))
3. 根 据 延 拓 h ~ 的 定 义 , 若 g ( x ) ∉ d o m h , 那 么 h ( g ( x ) ) = ∞ , 上 述 不 等 式 也 成 立 , 于 是 f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) , f 是 凸 函 数 3.根据延拓\tilde{h}的定义,若g(x)\notin domh,那么h(g(x))=\infty,上述不等式也成立,于是f(\theta x+(1-\theta)y)\leq\theta f(x)+(1-\theta)f(y),f是凸函数 3.根据延拓h~的定义,若g(x)∈/domh,那么h(g(x))=∞,上述不等式也成立,于是f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y),f是凸函数
例子:
- g ( x ) 是 凸 函 数 → exp g ( x ) 是 凸 函 数 g(x)是凸函数\rightarrow \exp{g(x)}是凸函数 g(x)是凸函数→expg(x)是凸函数
- g ( x ) 是 凹 函 数 , g ( x ) > 0 → 1 g ( x ) 是 凸 函 数 g(x)是凹函数,g(x)>0\rightarrow \frac{1}{g(x)}是凸函数 g(x)是凹函数,g(x)>0→g(x)1是凸函数
向量的耦合Vector composition
定义:
g : R n → R k , h : R k → R , f ( x ) = h ( g ( x ) ) = h ( g 1 ( x ) , g 2 ( x ) , . . . , g k ( x ) ) g:R^n\rightarrow R^k,h:R^k\rightarrow R,f(x)=h(g(x))=h(g_1(x),g_2(x),...,g_k(x)) g:Rn→Rk,h:Rk→R,f(x)=h(g(x))=h(g1(x),g2(x),...,gk(x))
回 顾 多 元 函 数 二 阶 导 数 因 子 : ▽ 2 f ( x ) i j = ∂ 2 f ( x ) ∂ x i ∂ x j 回顾多元函数二阶导数因子:\triangledown^2{f(x)_{ij}}=\frac{\partial^2{f(x)}}{\partial{x_i}\partial{x_j}} 回顾多元函数二阶导数因子:▽2f(x)ij=∂xi∂xj∂2f(x)
f ′ ′ ( x ) = g ′ ( x ) T ▽ 2 h ( g ( x ) ) g ′ ( x ) + ▽ h ( g ( x ) ) T g ′ ′ ( x ) f''(x)=g'(x)^T\triangledown^2{h(g(x))}g'(x)+\triangledown h(g(x))^Tg''(x) f′′(x)=g′(x)T▽2h(g(x))g′(x)+▽h(g(x))Tg′′(x)
[ 1 ] . g i 是 凸 函 数 , h 的 延 拓 h ~ 是 非 递 减 的 , h 是 凸 函 数 [1].g_i是凸函数,h的延拓\tilde{h}是非递减的,h是凸函数 [1].gi是凸函数,h的延拓h~是非递减的,h是凸函数
[ 2 ] . g i 是 凹 函 数 , h 的 延 拓 h ~ 是 非 递 增 的 , h 是 凸 函 数 [2].g_i是凹函数,h的延拓\tilde{h}是非递增的,h是凸函数 [2].gi是凹函数,h的延拓h~是非递增的,h是凸函数
→ f ( x ) 是 凸 函 数 ( f ′ ′ ( x ) ≥ 0 ) \rightarrow f(x)是凸函数(f''(x)\geq 0) →f(x)是凸函数(f′′(x)≥0)
例子:
- g i ( x ) 是 凹 函 数 , g i ( x ) > 0 → ∑ i = 1 m log g i ( x ) 是 凹 函 数 , 加 上 负 号 凹 凸 性 改 变 g_i(x)是凹函数,g_i(x)>0\rightarrow \sum\limits_{i=1}^m\log g_i(x)是凹函数,加上负号凹凸性改变 gi(x)是凹函数,gi(x)>0→i=1∑mloggi(x)是凹函数,加上负号凹凸性改变
- g i ( x ) 是 凸 函 数 → log ∑ i = 1 m exp g i ( x ) 是 凸 函 数 ( 二 阶 导 非 负 ) g_i(x)是凸函数\rightarrow \log{\sum\limits_{i=1}^m\exp g_i(x)}是凸函数(二阶导非负) gi(x)是凸函数→logi=1∑mexpgi(x)是凸函数(二阶导非负)
最小值Minimization
定义:
f ( x , y ) 对 ( x , y ) 都 满 足 凸 函 数 , C 是 凸 集 → g ( x ) = inf y ∈ C f ( x , y ) 是 凸 函 数 f(x,y)对(x,y)都满足凸函数,C是凸集\rightarrow g(x)=\inf\limits_{y\isin C}f(x,y)是凸函数 f(x,y)对(x,y)都满足凸函数,C是凸集→g(x)=y∈Cinff(x,y)是凸函数
例子:
高 维 倾 斜 二 次 型 函 数 : f ( x ) = x T A x + 2 x T B y + y T C y 高维倾斜二次型函数:f(x)=x^TAx+2x^TBy+y^TCy 高维倾斜二次型函数:f(x)=xTAx+2xTBy+yTCy
f ( x ) 的 二 阶 导 [ A B B T C ] ≥ 0 , C > 0 → f ( x ) 是 凸 函 数 f(x)的二阶导\begin{bmatrix}A & B \\ B^T & C\end{bmatrix}\geq 0,C>0\rightarrow f(x)是凸函数 f(x)的二阶导[ABTBC]≥0,C>0→f(x)是凸函数
f ( x , y ) 对 于 y 进 行 最 小 化 , g ( x ) = inf y ∈ C f ( x , y ) = x T ( A − B C − 1 B T ) x 根 据 保 凸 运 算 可 知 g 是 凸 函 数 , 所 以 其 系 数 矩 阵 ( 舒 尔 补 ) 是 半 正 定 的 ( A − B C − 1 B T ≥ 0 ) f(x,y)对于y进行最小化,g(x)=\inf\limits_{y\isin C}f(x,y)=x^T(A-BC^{-1}B^T)x根据保凸运算可知g是凸函数,所以其系数矩阵(舒尔补)是半正定的(A-BC^{-1}B^T\geq 0) f(x,y)对于y进行最小化,g(x)=y∈Cinff(x,y)=xT(A−BC−1BT)x根据保凸运算可知g是凸函数,所以其系数矩阵(舒尔补)是半正定的(A−BC−1BT≥0)
舒尔补Schur complement-n×n方阵分块
分块形式: M = [ A B C D ] n × n M=\begin{bmatrix}A & B \\ C & D\end{bmatrix}_{n\times n} M=[ACBD]n×n
其 中 A , D 是 方 阵 其中 A,D是方阵 其中A,D是方阵
A 是 非 奇 异 的 , 则 A 在 M 中 的 舒 尔 补 : D − C A − 1 B A是非奇异的,则A在M中的舒尔补:D-CA^{-1}B A是非奇异的,则A在M中的舒尔补:D−CA−1B(顺时针排列)
D 是 非 奇 异 的 , 则 D 在 M 中 的 舒 尔 补 : A − B D − 1 C D是非奇异的,则D在M中的舒尔补:A-BD^{-1}C D是非奇异的,则D在M中的舒尔补:A−BD−1C(顺时针排列)
本质:
A 是 非 奇 异 的 , 则 对 A 做 初 等 对 角 化 : [ I 0 − C A − 1 I ] [ A B C D ] [ I − A − 1 B 0 I ] = [ A 0 0 D − C A − 1 B ] A是非奇异的,则对A做初等对角化:\begin{bmatrix}I & 0 \\ -CA^{-1} & I\end{bmatrix}\begin{bmatrix}A & B \\ C & D\end{bmatrix}\begin{bmatrix}I & -A^{-1}B \\ 0 & I\end{bmatrix}=\begin{bmatrix}A & 0 \\ 0 & D-CA^{-1}B\end{bmatrix} A是非奇异的,则对A做初等对角化:[I−CA−10I][ACBD][I0−A−1BI]=[A00D−CA−1B]
得到行列式: ∣ A B C D ∣ = ∣ A 0 0 D − C A − 1 B ∣ = ∣ A ∣ ∣ D − C A − 1 B ∣ \begin{vmatrix}A & B \\ C & D\end{vmatrix}=\begin{vmatrix}A & 0 \\ 0 & D-CA^{-1}B\end{vmatrix}=|A||D-CA^{-1}B| ∣∣∣∣ACBD∣∣∣∣=∣∣∣∣A00D−CA−1B∣∣∣∣=∣A∣∣D−CA−1B∣
所以:
- ( A 非 奇 异 ) M 非 奇 异 ⟺ D − C A − 1 B 非 奇 异 (A非奇异)M非奇异\iff D-CA^{-1}B非奇异 (A非奇异)M非奇异⟺D−CA−1B非奇异
- ( D 非 奇 异 ) M 非 奇 异 ⟺ A − B D − 1 C 非 奇 异 (D非奇异)M非奇异\iff A-BD^{-1}C非奇异 (D非奇异)M非奇异⟺A−BD−1C非奇异
透射函数Perspective
定义:
f : R n → R , f 是 凸 函 数 , g : R n × R → R , d o m g = { ( x , t ) ∣ x t ∈ d o m f , t > 0 } → g ( x , t ) = t f ( x t ) 是 凸 函 数 f:R^n\rightarrow R,f是凸函数,g:R^n\times R\rightarrow R,domg=\{(x,t)|\frac{x}{t}\isin domf,t>0\}\rightarrow g(x,t)=tf(\frac{x}{t})是凸函数 f:Rn→R,f是凸函数,g:Rn×R→R,domg={(x,t)∣tx∈domf,t>0}→g(x,t)=tf(tx)是凸函数
例子:
- f ( x ) = x T x 是 凸 函 数 , t > 0 → g ( x , t ) = x T x t 是 凸 函 数 f(x)=x^Tx是凸函数,t>0\rightarrow g(x,t)=\frac{x^Tx}{t}是凸函数 f(x)=xTx是凸函数,t>0→g(x,t)=txTx是凸函数
- f ( x ) = − log x 是 凸 函 数 → g ( x , t ) = − t log x t 是 凸 函 数 , 在 R + + 2 集 合 上 f(x)=-\log{x}是凸函数\rightarrow g(x,t)=-t\log{\frac{x}{t}}是凸函数,在R_{++}^2集合上 f(x)=−logx是凸函数→g(x,t)=−tlogtx是凸函数,在R++2集合上
- f ( x ) 是 凸 函 数 , 定 义 域 { x ∣ c T x + d > 0 , ( A x + b ) C T x + d ∈ d o m f } → g ( x ) = ( c T x + d ) f ( A x + b c T x + d ) 是 凸 函 数 ( 仿 射 + 透 射 p e r s p e c t i v e ) f(x)是凸函数,定义域\{x|c^Tx+d>0,\frac{(Ax+b)}{C^Tx+d}\isin domf\}\rightarrow g(x)=(c^Tx+d)f(\frac{Ax+b}{c^Tx+d})是凸函数(仿射+透射perspective) f(x)是凸函数,定义域{x∣cTx+d>0,CTx+d(Ax+b)∈domf}→g(x)=(cTx+d)f(cTx+dAx+b)是凸函数(仿射+透射perspective)
小结
请跳转到最后的总结。
共轭函数Conjugate function
原函数是以x为自变量,求y值
共轭函数是以斜率为自变量,求y轴上截距值
找斜率的最小值 ⟺ \iff ⟺找y轴上截距的最大值
定义:
多元偏分函数形式:
切 线 : g ( x ) = ( x − x 0 ) ∂ f ∂ x ( x 0 ) + f ( x 0 ) ) 切线:g(x)=(x-x_0)\frac{\partial f}{\partial x}(x_0)+f(x_0)) 切线:g(x)=(x−x0)∂x∂f(x0)+f(x0))
截 距 : g ( 0 ) = − x 0 ∂ f ∂ x ( x 0 ) + f ( x 0 ) 截距:g(0)=-x_0\frac{\partial f}{\partial x}(x_0)+f(x_0) 截距:g(0)=−x0∂x∂f(x0)+f(x0)
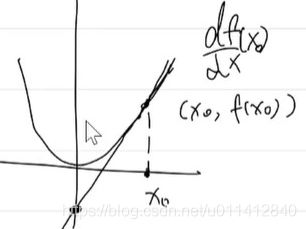
共轭形式:
共轭函数(截距的相反数): x = x 0 ∈ d o m f , 自 变 量 y = ∂ f ∂ x , f ∗ ( y ) = y T x − f ( x ) x=x_0\isin domf,自变量y=\frac{\partial f}{\partial x},f^*(y)=y^Tx-f(x) x=x0∈domf,自变量y=∂x∂f,f∗(y)=yTx−f(x)
f ( x ) 是 凸 函 数 , 所 以 y 和 − f ( x ) 是 凹 函 数 , 有 唯 一 最 大 值 f(x)是凸函数,所以y和-f(x)是凹函数,有唯一最大值 f(x)是凸函数,所以y和−f(x)是凹函数,有唯一最大值
求 最 值 的 目 标 函 数 : f ∗ ( y ) = sup x ∈ d o m f ( y T x − f ( x ) ) 求最值的目标函数:f^*(y)=\sup\limits_{x\isin domf}(y^Tx-f(x)) 求最值的目标函数:f∗(y)=x∈domfsup(yTx−f(x))
{ y = ∂ f ∂ x x = ∂ f ∗ ∂ y , 属 于 对 称 形 式 , 所 以 两 次 共 轭 会 回 到 原 来 的 函 数 \begin{cases}y=\frac{\partial f}{\partial x} \\ x=\frac{\partial f^*}{\partial y}\end{cases},属于对称形式,所以两次共轭会回到原来的函数 {y=∂x∂fx=∂y∂f∗,属于对称形式,所以两次共轭会回到原来的函数
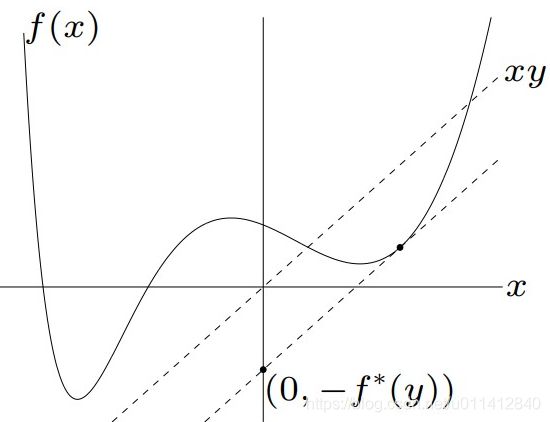
截 距 是 给 点 , 找 斜 线 求 截 距 最 大 值 截距是给点,找斜线求截距最大值 截距是给点,找斜线求截距最大值
共 轭 是 给 斜 线 , 找 点 求 截 距 最 大 值 , 且 即 使 f 不 是 凸 函 数 , f ∗ 也 是 凸 函 数 共轭是给斜线,找点求截距最大值,且即使f不是凸函数,f^*也是凸函数 共轭是给斜线,找点求截距最大值,且即使f不是凸函数,f∗也是凸函数
例子:
- f ( x ) = − log x , x > 0 → f ∗ ( y ) = sup x > 0 ( x y + log x ) f(x)=-\log x,x>0\rightarrow f^*(y)=\sup\limits_{x>0}(xy+\log x) f(x)=−logx,x>0→f∗(y)=x>0sup(xy+logx)
可 知 y = ∂ f ( x ) ∂ x , 最 值 即 导 数 y + 1 x = 0 , 所 以 x = − 1 y 可知y=\frac{\partial f(x)}{\partial x},最值即导数y+\frac{1}{x}=0,所以x=-\frac{1}{y} 可知y=∂x∂f(x),最值即导数y+x1=0,所以x=−y1
f ∗ ( y ) = { − 1 + log ( − 1 y ) y < 0 ∞ y ≥ 0 f^*(y)=\begin{cases} -1+\log{(-\frac{1}{y})} & y<0 \\ \infty & y\geq 0 \end{cases} f∗(y)={−1+log(−y1)∞y<0y≥0 - f ( x ) = 1 2 x T Q x , Q ∈ S + + n → f ∗ ( y ) = sup x ( y T x − 1 2 x T Q x ) ⟺ 计 算 二 次 函 数 的 极 值 f(x)=\frac{1}{2}x^TQx,Q\isin S_{++}^n\rightarrow f^*(y)=\sup\limits_{x}(y^Tx-\frac{1}{2}x^TQx)\iff计算二次函数的极值 f(x)=21xTQx,Q∈S++n→f∗(y)=xsup(yTx−21xTQx)⟺计算二次函数的极值
根 据 x = Q − 1 y 推 导 出 : f ∗ ( y ) = y T Q − 1 y − 1 2 y T Q − 1 y = 1 2 y T Q − 1 y , 这 形 式 与 f ( x ) 对 称 根据x=Q^{-1}y推导出: f^*(y)=y^TQ^{-1}y-\frac{1}{2}y^TQ^{-1}y=\frac{1}{2}y^TQ^{-1}y,这形式与f(x)对称 根据x=Q−1y推导出:f∗(y)=yTQ−1y−21yTQ−1y=21yTQ−1y,这形式与f(x)对称
类 比 能 量 公 式 : E = 1 2 m v 2 = 1 2 v m v → E ∗ ( p ) = 1 2 p 1 m p = p 2 2 m , p = m v 是 动 量 用 来 表 示 v 的 物 理 过 程 类比能量公式:E=\frac{1}{2}mv^2=\frac{1}{2}vmv\rightarrow E^*(p)=\frac{1}{2}p\frac{1}{m}p=\frac{p^2}{2m},p=mv是动量用来表示v的物理过程 类比能量公式:E=21mv2=21vmv→E∗(p)=21pm1p=2mp2,p=mv是动量用来表示v的物理过程
次凸函数Quasiconvex|次凹函数Quasiconcave
这类函数不全符合凸函数的定义,但是他们仍然有唯一最值
定义:
f : R n → R , d o m f 是 凸 集 , ∀ α , ( s u b l e v e l s e t ) S α = { x ∣ f ( x ) ≤ α } 是 凸 集 → f 是 次 凸 函 数 f:R^n\rightarrow R,domf是凸集,\forall\alpha,(sublevel\space set)S_\alpha=\{x|f(x)\leq\alpha\}是凸集\rightarrow f是次凸函数 f:Rn→R,domf是凸集,∀α,(sublevel set)Sα={x∣f(x)≤α}是凸集→f是次凸函数
f : R n → R , d o m f 是 凸 集 , ∀ α , ( h i g h l e v e l s e t ) H α = { x ∣ f ( x ) > α } 是 凸 集 → f 是 次 凹 函 数 f:R^n\rightarrow R,domf是凸集,\forall\alpha,(highlevel\space set)H_\alpha=\{x|f(x)>\alpha\}是凸集\rightarrow f是次凹函数 f:Rn→R,domf是凸集,∀α,(highlevel set)Hα={x∣f(x)>α}是凸集→f是次凹函数
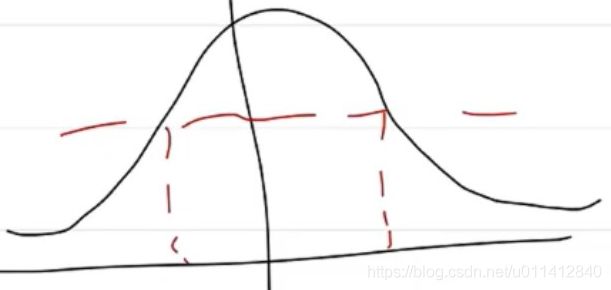
判定:
- − f 是 次 凸 函 数 → f 是 次 凹 函 数 -f是次凸函数\rightarrow f是次凹函数 −f是次凸函数→f是次凹函数
- f 是 次 凹 函 数 也 是 次 凸 函 数 → f 是 次 线 性 函 数 f是次凹函数也是次凸函数\rightarrow f是次线性函数 f是次凹函数也是次凸函数→f是次线性函数
例子:
-
x ∈ R , f = ∣ x ∣ 是 次 凸 函 数 x\isin R,f=\sqrt{|x|}是次凸函数 x∈R,f=∣x∣是次凸函数
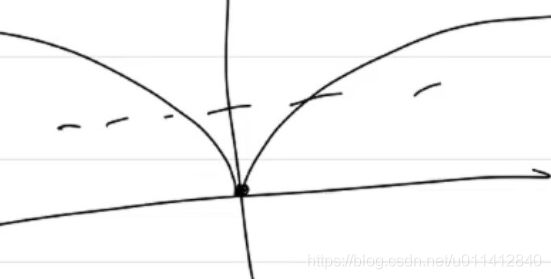
-
f = c e i l ( x ) = i n f { z ∈ Z ∣ z ≥ x } 是 次 线 性 函 数 f=ceil(x)=inf\{z\isin Z|z\geq x\}是次线性函数 f=ceil(x)=inf{z∈Z∣z≥x}是次线性函数

-
x ∈ R + + , f = log x 是 次 线 性 函 数 x\isin R_{++},f=\log x是次线性函数 x∈R++,f=logx是次线性函数

-
x ∈ R + + 2 , f ( x 1 , x 2 ) = x 1 x 2 是 次 凹 函 数 x\isin R_{++}^2,f(x_1,x_2)=x_1x_2是次凹函数 x∈R++2,f(x1,x2)=x1x2是次凹函数
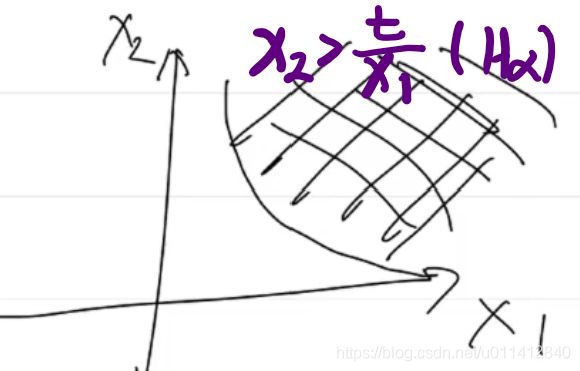
-
d o m f = { x ∣ c T x + d > 0 } , f ( x ) = a T x + b x T x + d 是 次 线 性 函 数 domf=\{x|c^Tx+d>0\},f(x)=\frac{a^Tx+b}{x^Tx+d}是次线性函数 domf={x∣cTx+d>0},f(x)=xTx+daTx+b是次线性函数(linear-fractional-function)
-
d o m f = { x ∣ ∣ ∣ x − a ∣ ∣ 2 ≤ ∣ ∣ x − b ∣ ∣ 2 } , f ( x ) = ∣ ∣ x − a ∣ ∣ 2 ∣ ∣ x − b ∣ ∣ 2 是 次 凸 函 数 domf=\{x|\space ||x-a||_2\leq||x-b||_2\},f(x)=\frac{||x-a||_2}{||x-b||_2}是次凸函数 domf={x∣ ∣∣x−a∣∣2≤∣∣x−b∣∣2},f(x)=∣∣x−b∣∣2∣∣x−a∣∣2是次凸函数
性质:
-
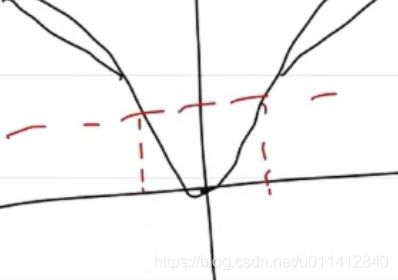
modified Jensen inequality: f 是 次 凸 函 数 θ ∈ [ 0 , 1 ] → f ( θ x + ( 1 − θ ) y ) ≤ max ( f ( x ) , f ( y ) ) f是次凸函数\theta\isin [0,1]\rightarrow f(\theta x+(1-\theta)y)\leq\max{(f(x),f(y))} f是次凸函数θ∈[0,1]→f(θx+(1−θ)y)≤max(f(x),f(y))
【下图是不符合条件的多峰情况】

-
first-order condition: f 定 义 域 是 凸 集 , f 可 微 是 次 凸 函 数 ⟺ f ( y ) ≤ f ( x ) ⟹ ▽ f ( x ) T ( y − x ) ≤ 0 f定义域是凸集,f可微是次凸函数\iff f(y)\leq f(x)\implies \triangledown f(x)^T(y-x)\leq 0 f定义域是凸集,f可微是次凸函数⟺f(y)≤f(x)⟹▽f(x)T(y−x)≤0
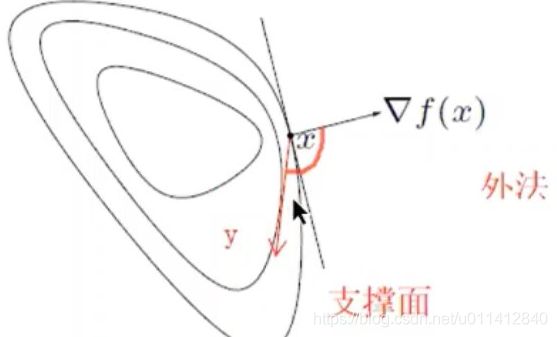
-
次凸函数的累加,不一定仍是次凸函数
取log意义下的凹函数log-concave和凸函数log-convex
定义:
log f 是 凸 函 数 → f 是 l o g − c o n v e x 函 数 : θ ∈ [ 0 , 1 ] , f ( θ x + ( 1 − θ ) y ) ≤ f ( x ) θ f ( y ) 1 − θ \log{f}是凸函数\rightarrow f是log-convex函数:\theta\isin[0,1],f(\theta x+(1-\theta)y)\leq f(x)^{\theta}f(y)^{1-\theta} logf是凸函数→f是log−convex函数:θ∈[0,1],f(θx+(1−θ)y)≤f(x)θf(y)1−θ
log f 是 凹 函 数 → f 是 l o g − c o n c a v e 函 数 : θ ∈ [ 0 , 1 ] , f ( θ x + ( 1 − θ ) y ) ≥ f ( x ) θ f ( y ) 1 − θ \log{f}是凹函数\rightarrow f是log-concave函数:\theta\isin[0,1],f(\theta x+(1-\theta)y)\geq f(x)^{\theta}f(y)^{1-\theta} logf是凹函数→f是log−concave函数:θ∈[0,1],f(θx+(1−θ)y)≥f(x)θf(y)1−θ
公式理解:
log f ( θ x + ( 1 − θ ) y ) ≤ θ log f ( x ) + ( 1 − θ ) log f ( y ) \log{f(\theta x+(1-\theta)y)}\leq \theta\log{f(x)}+(1-\theta)\log{f(y)} logf(θx+(1−θ)y)≤θlogf(x)+(1−θ)logf(y)
= log f ( x ) θ + log f ( y ) 1 − θ =\log{f(x)^{\theta}}+\log{f(y)^{1-\theta}} =logf(x)θ+logf(y)1−θ
= log f ( x ) θ f ( y ) 1 − θ =\log{f(x)^{\theta}f(y)^{1-\theta}} =logf(x)θf(y)1−θ
例子:
( 次 凹 函 数 ) 高 斯 函 数 f ( x ) = e − x 2 → ( 凹 函 数 ) log f ( x ) = − x 2 (次凹函数)高斯函数f(x)=e^{-x^2}\rightarrow (凹函数)\log{f(x)}=-x^2 (次凹函数)高斯函数f(x)=e−x2→(凹函数)logf(x)=−x2
( l o g − c o n c a v e 函 数 ) 高 斯 分 布 : Φ ( x ) = ∫ − ∞ x 1 2 π e − u 2 2 d x (log-concave函数)高斯分布:\Phi(x)=\int_{-\infty}^x\frac{1}{\sqrt{2\pi}}e^{-\frac{u^2}{2}}dx (log−concave函数)高斯分布:Φ(x)=∫−∞x2π1e−2u2dx
f ( x ) = x α , x ∈ R + + , ( 1 ) α ≤ 0 , f ( x ) 是 l o g − c o n v e x ; ( 2 ) α ≥ 0 , f ( x ) 是 l o g − c o n c a v e f(x)=x^{\alpha},x\isin R_{++},(1)\alpha\leq 0,f(x)是log-convex;(2)\alpha\geq 0,f(x)是log-concave f(x)=xα,x∈R++,(1)α≤0,f(x)是log−convex;(2)α≥0,f(x)是log−concave
性质&特殊log操作:
f 二 阶 可 导 , d o m f 是 凸 集 f二阶可导,domf是凸集 f二阶可导,domf是凸集
- f 是 l o g − c o n c a v e ( c o n v e x ) ⟺ ▽ 2 f ( x ) ≤ ( ≥ ) ▽ f ( x ) ▽ f ( x ) T f ( x ) f是log-concave(convex)\iff \triangledown^2f(x)\leq(\geq)\frac{\triangledown f(x)\triangledown f(x)^T}{f(x)} f是log−concave(convex)⟺▽2f(x)≤(≥)f(x)▽f(x)▽f(x)T
- Product of log-concave functions is also log-concave: f ( x ) , g ( x ) 都 是 l o g − c o n c a v e , 那 么 log f ( x ) 和 log g ( x ) 就 是 c o n c a v e , 所 以 log f ( x ) + log g ( x ) = log ( f ( x ) g ( x ) ) 是 c o n c a v e , f ( x ) g ( x ) 是 l o g − c o n c a v e f(x),g(x)都是log-concave,那么\log{f(x)}和\log{g(x)}就是concave,所以\log{f(x)}+\log{g(x)}=\log{(f(x)g(x))}是concave,f(x)g(x)是log-concave f(x),g(x)都是log−concave,那么logf(x)和logg(x)就是concave,所以logf(x)+logg(x)=log(f(x)g(x))是concave,f(x)g(x)是log−concave
- Sum of log-concave functions is not always log-concave: log ( f ( x ) + g ( x ) ) \log{(f(x)+g(x))} log(f(x)+g(x))
- Integration积分意义下保凸: f : R n × R m → R 是 l o g − c o n c a v e → g ( x ) = ∫ f ( x , y ) d y 是 l o g − c o n c a v e f:R^n\times R^m\rightarrow R是log-concave\rightarrow g(x)=\int f(x,y)dy是log-concave f:Rn×Rm→R是log−concave→g(x)=∫f(x,y)dy是log−concave
- Convolution卷积意义下: f ( x ) , g ( x ) 都 是 l o g − c o n c a v e → ( f ∗ g ) ( x ) = ∫ f ( x − y ) g ( y ) d y 是 l o g − c o n c a v e f(x),g(x)都是log-concave\rightarrow (f*g)(x)=\int f(x-y)g(y)dy是log-concave f(x),g(x)都是log−concave→(f∗g)(x)=∫f(x−y)g(y)dy是log−concave
广义不等关系的凸性
定义:
recall: x − y ∈ K ⟺ y ≤ K x x-y\isin K\iff y\leq_K x x−y∈K⟺y≤Kx
f : R n → R m 是 K − c o n v e x ( K 锥 型 ) , d o m f 是 凸 集 , θ ∈ [ 0 , 1 ] , f ( θ x + ( 1 − θ ) y ) ≤ K θ f ( x ) + ( 1 − θ ) f ( y ) f:R^n\rightarrow R^m是K-convex(K锥型),domf是凸集,\theta\isin[0,1],f(\theta x+(1-\theta)y)\leq_K \theta f(x)+(1-\theta)f(y) f:Rn→Rm是K−convex(K锥型),domf是凸集,θ∈[0,1],f(θx+(1−θ)y)≤Kθf(x)+(1−θ)f(y)
举例:
f : S m → S m , f ( x ) = X 2 是 S + m − c o n v e x ( 对 称 半 正 定 凸 函 数 ) f:S^m\rightarrow S^m,f(x)=X^2是S_+^m-convex(对称半正定凸函数) f:Sm→Sm,f(x)=X2是S+m−convex(对称半正定凸函数)
证 明 部 分 1. 对 称 半 正 定 阵 : 找 一 个 向 量 v , 使 得 v T A v ≥ 0 : ∀ z , z T X 2 z = z T X T X z = ( X z ) T X z = ∣ ∣ X z ∣ ∣ 2 2 ( 2 类 范 数 ) 是 凸 集 ( 成 立 ) 证明部分1. 对称半正定阵:找一个向量v,使得v^TAv\geq 0:\forall z,z^TX^2z=z^TX^TXz=(Xz)^TXz=||Xz||_2^2(2类范数)是凸集(成立) 证明部分1.对称半正定阵:找一个向量v,使得vTAv≥0:∀z,zTX2z=zTXTXz=(Xz)TXz=∣∣Xz∣∣22(2类范数)是凸集(成立)
证 明 部 分 2. c o n v e x : z T ( θ X + ( 1 − θ ) Y ) 2 z ≤ θ z T X 2 z + ( 1 − θ ) z T Y 2 z ⟹ z T ( θ X 2 + ( 1 − θ ) Y 2 − ( θ X + ( 1 − θ ) Y ) 2 ) z ≥ 0 , 所 以 需 要 条 件 ( θ X + ( 1 − θ ) Y ) 2 ≤ θ X 2 + ( 1 − θ ) Y 2 ( 一 般 意 义 下 的 凸 关 系 成 立 ) 证明部分2. convex:z^T(\theta X+(1-\theta)Y)^2z\leq \theta z^TX^2z+(1-\theta)z^TY^2z\implies z^T(\theta X^2+(1-\theta)Y^2-(\theta X+(1-\theta)Y)^2)z\geq 0,所以需要条件(\theta X+(1-\theta)Y)^2\leq \theta X^2+(1-\theta)Y^2(一般意义下的凸关系成立) 证明部分2.convex:zT(θX+(1−θ)Y)2z≤θzTX2z+(1−θ)zTY2z⟹zT(θX2+(1−θ)Y2−(θX+(1−θ)Y)2)z≥0,所以需要条件(θX+(1−θ)Y)2≤θX2+(1−θ)Y2(一般意义下的凸关系成立)
总结
-
判定一个凸函数的3种方法:
- 定义法
- 凸函数符合Jensen不等式, ∀ x , y ∈ d o m f , ∀ θ ∈ [ 0 , 1 ] , f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) \forall x,y\isin domf,\forall \theta\isin[0,1],f(\theta x+(1-\theta)y)\leq\theta f(x)+(1-\theta)f(y) ∀x,y∈domf,∀θ∈[0,1],f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)
- 凸函数等价定义:(高维限制) ∃ g ( t ) = f ( x + t v ) , f 是 凸 函 数 , d o m g = { t ∣ x + t v ∈ d o m f } \exists g(t)=f(x+tv),f是凸函数,dom g=\{t|x+tv\isin domf\} ∃g(t)=f(x+tv),f是凸函数,domg={t∣x+tv∈domf}
凸函数可以延拓到 R n R^n Rn上,保持凸性,并且区分不同定义域的取值方式。 - 一次微分函数, f ( y ) ≥ f ( x ) + ▽ f ( x ) T ( y − x ) f(y)\geq f(x)+\triangledown{f(x)^T}(y-x) f(y)≥f(x)+▽f(x)T(y−x)
就是函数图像在某个点切线之上,高维情况要运用凸函数等价定义(高维限制)。 - epi图判定,epi函数是凸的
sublevel set 和 epigraph都是判定凸函数的充分条件
- 二次微分函数, ▽ 2 f ( x ) ≥ 0 \triangledown^2{f(x)}\geq 0 ▽2f(x)≥0
高维情况,就是函数二阶导的矩阵是半正定的 - 保凸运算(该部分的小结)
- 非负权和nonegative weight sum
1. α i ≥ 0 , f i 是 凸 函 数 → f ( x ) = ∑ i = 1 k α i f i 是 凸 函 数 1.\alpha_i\geq 0,f_i是凸函数\rightarrow f(x)=\sum\limits_{i=1}^k\alpha_if_i是凸函数 1.αi≥0,fi是凸函数→f(x)=i=1∑kαifi是凸函数(线性变换保凸)
2. f ( x ) 是 凸 函 数 , ∀ y , w ( y ) ≥ 0 → g ( x ) = ∫ Ω f ( x , y ) w ( y ) d y 是 凸 函 数 2.f(x)是凸函数,\forall y,w(y)\geq 0\rightarrow g(x)=\int_\Omega f(x,y)w(y)dy是凸函数 2.f(x)是凸函数,∀y,w(y)≥0→g(x)=∫Ωf(x,y)w(y)dy是凸函数 - 仿射函数复合composition with affine function
f ( x ) 是 凸 函 数 → f ( A x + b ) 是 凸 函 数 f(x)是凸函数\rightarrow f(Ax+b)是凸函数 f(x)是凸函数→f(Ax+b)是凸函数 - 逐点最大pointwise maximum and 逐点上界pointwise supremum
有 限 个 f 1 ( x ) , . . . , f m ( x ) 是 凸 函 数 → f ( x ) = m a x { f 1 ( x ) , . . . , f m ( x ) } 是 凸 函 数 有限个f_1(x),...,f_m(x)是凸函数\rightarrow f(x)=max\{f_1(x),...,f_m(x)\}是凸函数 有限个f1(x),...,fm(x)是凸函数→f(x)=max{f1(x),...,fm(x)}是凸函数
对 无 穷 个 点 , ∀ y ∈ A , f ( x , y ) 对 x 是 凸 函 数 → g ( x ) = sup y ∈ A f ( x , y ) 是 凸 函 数 ( g 是 f 关 于 y 求 极 值 的 函 数 ) 对无穷个点,\forall y\isin A,f(x,y)对x是凸函数\rightarrow g(x)=\sup\limits_{y\isin A}f(x,y)是凸函数(g是f关于y求极值的函数) 对无穷个点,∀y∈A,f(x,y)对x是凸函数→g(x)=y∈Asupf(x,y)是凸函数(g是f关于y求极值的函数) - composition耦合(复合)
标量函数的耦合: g : R n → R , h : R → R , f ( x ) = h ( g ( x ) ) 是 凸 函 数 ( f ′ ′ ( x ) ≥ 0 ) g:R^n\rightarrow R,h:R\rightarrow R,f(x)=h(g(x))是凸函数(f''(x)\geq 0) g:Rn→R,h:R→R,f(x)=h(g(x))是凸函数(f′′(x)≥0)
[ 1 ] . g 是 凸 函 数 ( g ′ ′ ≥ 0 ) , h 的 延 拓 h ~ 是 非 递 减 的 ( h ′ ≥ 0 ) , h 是 凸 函 数 ( f ′ ′ ≥ 0 ) [1].g是凸函数(g''\geq 0),h的延拓\tilde{h}是非递减的(h'\geq 0),h是凸函数(f''\geq 0) [1].g是凸函数(g′′≥0),h的延拓h~是非递减的(h′≥0),h是凸函数(f′′≥0)
[ 2 ] . g 是 凹 函 数 ( g ′ ′ ≤ 0 ) , h 的 延 拓 h ~ 是 非 递 增 的 ( h ′ ≤ 0 ) , h 是 凸 函 数 ( f ′ ′ ≥ 0 ) [2].g是凹函数(g''\leq 0),h的延拓\tilde{h}是非递增的(h'\leq 0),h是凸函数(f''\geq 0) [2].g是凹函数(g′′≤0),h的延拓h~是非递增的(h′≤0),h是凸函数(f′′≥0)
向量的耦合: g : R n → R k , h : R k → R , f ( x ) = h ( g ( x ) ) = h ( g 1 ( x ) , g 2 ( x ) , . . . , g k ( x ) ) 是 凸 函 数 g:R^n\rightarrow R^k,h:R^k\rightarrow R,f(x)=h(g(x))=h(g_1(x),g_2(x),...,g_k(x))是凸函数 g:Rn→Rk,h:Rk→R,f(x)=h(g(x))=h(g1(x),g2(x),...,gk(x))是凸函数
[ 1 ] . g i 是 凸 函 数 , h 的 延 拓 h ~ 是 非 递 减 的 , h 是 凸 函 数 [1].g_i是凸函数,h的延拓\tilde{h}是非递减的,h是凸函数 [1].gi是凸函数,h的延拓h~是非递减的,h是凸函数
[ 2 ] . g i 是 凹 函 数 , h 的 延 拓 h ~ 是 非 递 增 的 , h 是 凸 函 数 [2].g_i是凹函数,h的延拓\tilde{h}是非递增的,h是凸函数 [2].gi是凹函数,h的延拓h~是非递增的,h是凸函数 - 最小值minimization
f ( x , y ) 对 ( x , y ) 都 满 足
- 非负权和nonegative weight sum
- 定义法
