LeetCode1326.灌溉花园最少水龙头数目 (hard)总结

1326.灌溉花园最少水龙头数目

link

问题描述：

在 x 轴上有一个一维的花园。花园长度为 n，从点 0 开始，到点 n 结束。

花园里总共有 n + 1 个水龙头，分别位于 [0, 1, …, n] 。

给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ，其中 ranges[i] （下标从 0 开始）表示：如果打开点 i 处的水龙头，可以灌溉的区域为 [i - ranges[i], i + ranges[i]] 。

请你返回可以灌溉整个花园的 最少水龙头数目 。如果花园始终存在无法灌溉到的地方，请你返回 -1 。

示例 1：

输入：n = 5, ranges = [3,4,1,1,0,0]
输出：1
解释：
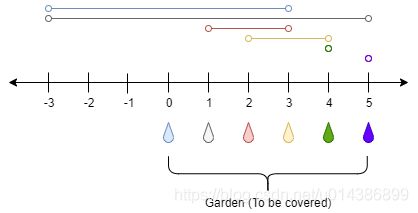
点 0 处的水龙头可以灌溉区间 [-3,3]
点 1 处的水龙头可以灌溉区间 [-3,5]
点 2 处的水龙头可以灌溉区间 [1,3]
点 3 处的水龙头可以灌溉区间 [2,4]
点 4 处的水龙头可以灌溉区间 [4,4]
点 5 处的水龙头可以灌溉区间 [5,5]
只需要打开点 1 处的水龙头即可灌溉整个花园 [0,5] 。

示例 2：

输入：n = 3, ranges = [0,0,0,0]
输出：-1
解释：即使打开所有水龙头，你也无法灌溉整个花园。

示例 3：

输入：n = 7, ranges = [1,2,1,0,2,1,0,1]
输出：3

示例 4：

输入：n = 8, ranges = [4,0,0,0,0,0,0,0,4]
输出：2

示例 5：

输入：n = 8, ranges = [4,0,0,0,4,0,0,0,4]
输出：1

提示：

1 <= n <= 10^4
ranges.length == n + 1
0 <= ranges[i] <= 100

解答

方法一： 贪婪法（最好的法）

查考的这个网友的答案，只是感觉该楼主解释的不好理解，所以，下面我写一下我的理解，这样理解更好明白：

作者解释中有两点是不容易理解的

1. land[i]的index 代表什么？它代表着每块土地，例如 index = 0，就代表土地0-1；index = 1，就代表土地 1-2；
2. 为什么要从 left~right 范围内搜索？因为当我们遍历每个位置时，每个位置都有它的覆盖范围，在这个覆盖范围内，如果之前有位置它的最远喷射距离比当前水龙头所能到达的距离小，那么，该位置所能喷射的最远距离就会更新为当前水龙头所能喷射的最右边界。

原作者解释：

解题思路：

1. n 代表土地数量（0 - 1 之间是一块地，1 - 2 之间是一块地）
2. n + 1 代表水龙头数量，水龙头插在数字上
3. ranges 代表当前位置的水龙头，向左向右可以覆盖多少块地
4. 定义一个 land 数据
   41. 代表在所有能够覆盖这块土地的所有水龙头中，找到能够覆盖最远（右边）位置的水龙头，记录它最右覆盖的土地
   42. 比如图例中，索引 0 代表覆盖了 0 - 1 之间这块地的所有水龙头里能够覆盖到最右的土地
   43. 值是 5 ，代表覆盖到最右边的是 4 - 5 这块土地
   索引是水龙头右边的那块地，而值是水龙头左边的那块地
   因此下面代码中 cur = land[cur]; 表示无缝的覆盖过去
   将 ranges 转换为 land 数据
5. 遍历 ranges ，解析其范围，将范围内的 land 更新为最大值
   从土地 0 开始，一直到土地 n ，记录水龙头数目

代码：

int minTaps(int n, vector& ranges) 
{
	vector land(n);
	for (int i = 0; i < ranges.size(); i++)
	{
		int l = max(i - ranges[i], 0);
		int r = min(i + ranges[i], n);
		for (int j = l; j < r; j++)
		{
			land[j] = max(land[j], r);
		}
	}

	int cnt = 0;
	int cur = 0;
	while (cur < n)
	{
		if (land[cur] == 0) return -1; //中间有土地没有被灌溉到
		cur = land[cur];
		cnt++;
	}
	return cnt;
}

方法二：结合各路网友后，我的代码思路
这种方法想起来是最容易理解的：

1. 先根据ranges，把各个位置覆盖范围的左边界和右边界求出来，也可以和下面的遍历合为一体，不过这样容易理解，得到一个数组mask.
2. 将 mask 按照左边界从小到大排序，如果遇到左边界相等，则按照右边界从小到大排序；
3. 从0开始往右找最合适的水龙头，什么才是最合适的呢？每一次循环总是找这样一个水龙头：
   • 它的左边界比上一轮循环的最远距离小，这样的话就保证了它与上一次无缝连接，再就是保证这个水龙头的有边界要比上次的最远距离大，不然这个水龙头是没有用的，上一次所能灌溉到的最远距离用 pos 表示，也就是这一轮查找的起始位置；
   • 用 farthest 记录每一轮循环所能灌溉到的最右边的距离；在 farthest < n 范围内，就继续往下找。
   • 在 mask 中由于前面的都比当前位置小，所以搜索时应该从上次搜索到的最合适的那个水龙头的index开始搜索，用 Index 来记录它。
4. 使用 hasFind 记录每次查找最优水龙头的结果，如果没找到则返回 -1。
5. 最后每次找到最优的水龙头时，count都加一，返回count;

代码：

class Solution {
public:
    int minTaps(int n, vector& ranges) {
        if(n == 0) return -1;
        
        // 排序
        vector> mask;

        for(int i = 0; i <= n; ++i){
            mask.push_back(make_pair(i - ranges[i], i + ranges[i]));
        }
        
        sort(mask.begin(), mask.end(), [](pair& p1, pair& p2){
            return p1.first < p2.first || ((p1.first == p2.first) && p1.second < p2.second);
        });
        
        int count = 0;
        
        // find the appropriate taps
        int Index = 0; // record the start pos in mask at the last round
        int farthest  = 0; // record int this round the farthest we can water
        int pos = 0; // record the last pos
        
        while(farthest < n){
            bool hasFind = false;
            for(int j = Index; j <= n; ++j){
                if(mask[j].first <= pos && mask[j].second > farthest){
                    farthest = mask[j].second;
                    hasFind = true;
                    Index = j;
                }
                else if(mask[j].first > pos){
                    break;
                }
            }
            pos = farthest;
            if(!hasFind) return -1;
            ++count;
        }
        
        return count == 0? -1 : count;
    }
};

方法三： 动态规划
官方答案中将的动态规划的思路，跟上面贪心的思路正好反过来了，即，
他是比较右端点，对于每一个右端点，寻找左端点最左的那个区间。具体来讲：
对于 0~n 的每一个点，假如我们从右往左看，
使用 prev[i] 代表在位置 i 处，当我们把 i 作为右端点时，prev[i]就是所能覆盖到的最左端点。
那么，我们使用 dp[i] 表示灌溉 [0, i] 范围所需的最少水龙头数目。

难理解的点：prev[i] 的构建，原文：
对于每一个区间 [li, ri]，我们将其绑定在它的右端点 ri 上，即 prev(i) = li 表示有一个区间为 [li, ri]。当多个区间有相同的 ri 时，我们将最长的那个区间作为 ri 的绑定区间，这是因为在选取区间时，如果区间的右端点固定，选取长的区间一定更优。如果某一个位置 rx 没有被绑定区间，那么我们给它赋予默认值 prev(rx) = rx，表示有一个区间为 [rx, rx]，它只覆盖了花园中的一个点，不可能作为答案的一部分，因此这个区间是无效的。
对应的代码：

 for (int i = 0; i <= n; ++i) {
          int l = max(i - ranges[i], 0);
          int r = min(i + ranges[i], n);
          prev[r] = min(prev[r], l);
       }

整个代码：

class Solution {
public:
    int minTaps(int n, vector& ranges) {
        vector prev(n + 1);
        iota(prev.begin(), prev.end(), 0);

        for (int i = 0; i <= n; ++i) {
            int l = max(i - ranges[i], 0);
            int r = min(i + ranges[i], n);
            prev[r] = min(prev[r], l);
        }

        vector dp(n + 1, INT_MAX);
        dp[0] = 0;
        for (int i = 1; i <= n; ++i) {
            for (int j = prev[i]; j < i; ++j) {
                if (dp[j] != INT_MAX) {
                    dp[i] = min(dp[i], dp[j] + 1);
                }
            }
        }

        return (dp[n] == INT_MAX ? -1 : dp[n]);
    }
};