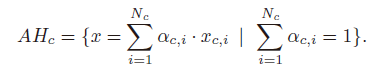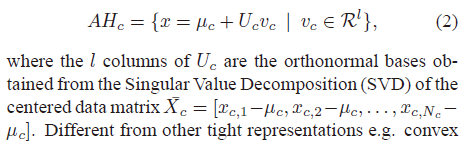将每个图像集表示为三态组合包括样本图样、 样本均值 、 样本图像集的仿射组合来覆盖样本图像的所有可能的仿射组合,这样一个仿射包的松散表示能够计算对于任何仿射组合在样本图像中没有出现的不可见的外观。与此同时,也对不同图像集之间的匹配引入了新的挑战。因为仿射包太大导致不同图像集之间的仿射包出现交叉从而使匹配失败。
为了解决上述问题,提出了SANP(稀疏近似最近点的方法)
相关知识点:
1)稀疏近似最近点(SANPs)可以由各自的样本图像稀疏地近似单独表示。
方法:
使用样本数据Xc,设计一种图像集在高维特征空间的线性模型来近似图像集结构。图像集仿射包建模如下:
引入样本均值,仿射包的模型被重写:
Uc是中心数据Xc经过奇异值分解(SVD)得到的标准正交基,与其他的紧密表示不同,任何仿射组合,即使组合并没有在集合样本中出现也能适应样本表示。这种松散的模型尤其对小样本集合友好,那些在属于集合但是没有出现的数据可以被很好的建模。同时,因为仿射包太大导致不同图像集之间的仿射包出现交叉从而使匹配失败。
SANP将图像集建模为一个三元组合(样本均值uc,标准正交基Uc,图像集Xc),包含结构信息和样本图片。
SANPs是稀疏近似最近点中的两个点,每个在各自个体集合中,满足以下约束:
1)这两点之间的欧几里得距离小
2)这两个点中的每一个都应该可以通过相应的图像集中少量的样本图像组合来近似(这个约束提高了SANPS的判别能力)
对于稀疏近似的约束使SANPs在仿射包的某些方面更加接近,从而是在在这些方面上更加接近一些样本图像。通过这个约束,虚假的图像集的最近点类是可以避免的。
为了找到两个图像集的SANPs,就上述两个约束,我们提出了一个凸规则:
Fv,v表示两个图像集之间的距离,G,Q表示原始图像集和建模的仿射包之间的偏差。
通过上述最小化问题得到和SANPs有关的重要参数值。第一项保证SANPs,(xi=ui+Uivi,xj=uj+Ujvj)最小,第二项是保证这两个点和他们样本近似之间的联系,最后两项保证近似是稀疏的,λ是平衡系数控制不同项之间的相对重要性。λ1固定为0.01,λ2和λ3设计一种自动调节机制来控制α和β的相对稀疏性。
Note:
1)匹配样本时,系数模型已经设计好了,
2)并没有在公式中的模型系数vi,vj上施加稀疏约束,Ui和Uj通过SVD得到,没有与示例数据点对齐,但却在样本系数α和β上施加稀疏约束。这意味着每一个最近的点都是由几个样本的组合图像稀疏地近似。不同于单一图像的稀疏建模分类,公式共同优化了两个图像集之间的最近点和从样本它们稀疏的近似。
优化;
函数前两项是光滑的,记为f(ν1,ν2,α,β),后两项是非光滑的,记为g(α,β)。很明显g(α,β)是有关α,β的凸函数(数学上的凸函数对应于凹函数),同时光滑函数f( )也是关于他参数的凸函数,由于目标函数是凸函数,因此可以得到全局最小值。