二叉搜索树(BST)学习笔记(一)
看完邓俊辉的《数据结构(第三版)》中二叉搜索树BST后的学习总结
二叉搜索树(Binary Search Tree)
一.循关键码访问call-by-key
1.二叉搜索树由一组数据项构成,数据项之间,依照各自的关键码key彼此区分。类似
于汽车的车牌号。
2.关键码之间支持大小比较与相等比对。
3.数据集合中的数据项统一地表示和实现为词条entry形式。
二.二叉搜索树的特性
二叉搜索树由节点构成,每个节点中都各自存有一个词条,每一个词条都唯一的对
应于某一个关键码。为了不混淆,往往将节点-词条-关键码这三个概念等同起来,相
互指代,不加严格区分。
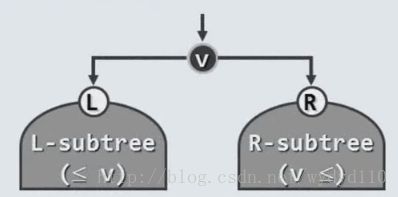
1.顺序性:任一节点均不小于/不大于其左/右后代
2.单调性:BST的中序遍历序列,必然单调非降
总结:BST微观上处处满足顺序性,宏观上整体满足单调性。BST的中序遍历序列,
必然单调非降。最左的为最小的,最右的为最大的。
对于遇到的每个结点x,都会比较x.key与根节点的大小,如果相等,就终止查找,否
则,决定是继续往左子树还是右子树查找。因此,整个查找过程就是从根节点开始一
直向下的一条路径,若假设树的高度是h,那么查找过程的时间复杂度就是O(h)。
3.接口:
1)search()
2)insert()
3)remove()
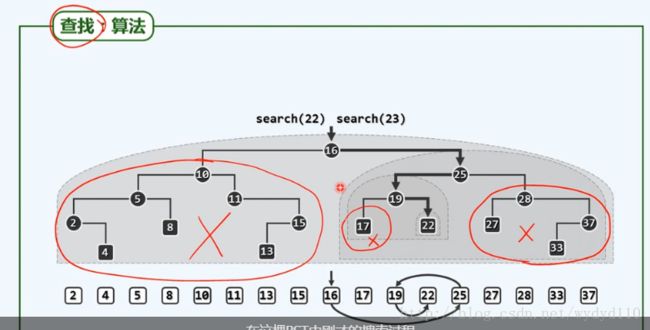
三.二叉搜索树的查找
查找22,22>16,跳到16的右子树,22<25,跳到25的左子树,22>19,跳到19的右子树,找到了22。
四.二叉搜索树的查找的Java实现
参考:http://blog.csdn.net/qq_21688757/article/details/53843724
public class TreeNode {
private int val;
private TreeNode leftChild;private TreeNode rightChild;
private TreeNode parent;
}
/**
* 非递归查找方式
*/
public TreeNode Search(TreeNode root,int key){
if(root==null){return null;
}
TreeNode pNode = root;
while (pNode != null && pNode.val != key) {
if (key < pNode.val) {
pNode = pNode.leftChild;
} else {
pNode = pNode.rightChild;
}}
return pNode;
}
/**
* 获取二叉查找树中的最小关键字结点(最左端)
*/
public TreeNode minElemNode(TreeNode node) {
if (node == null) {
return null;
}
TreeNode pNode = node;
while (pNode.leftChild != null) {
pNode = pNode.leftChild;
}return pNode;
}
/**
* maxElemNode: 获取二叉查找树中的最大关键字结点
*/
public TreeNode maxElemNode(TreeNode node) {
if (node == null) {
return null ;
}
TreeNode pNode = node;
while (pNode.rightChild != null) {
pNode = pNode.rightChild;
}return pNode;
}
}
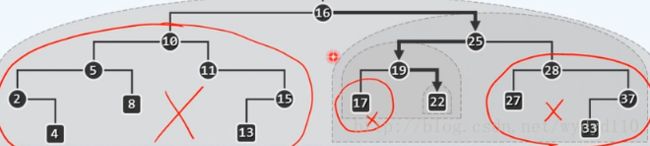
/**
* successor: 获取给定结点在中序遍历顺序下的后继结点
中序遍历二叉树得到的是递增序列,所以后继结点就是递增序列中该结点的下一位
* 1.该结点有右子树,则右子数中最小值即为该结点后继结点
11 -13
* 2.该结点无右子树且该结点是父节点的左子树,则该节点的父节点则为后继结点
27 - 28
* 3.该结点无右子树且该结点是父节点的右子树,则不断往父节点遍历。
15
*/
public TreeNode successor(TreeNode node) throws Exception {
if (node == null) {
return null;
}
// 若该结点的右子树不为空,则其后继结点就是右子树中的最小关键字结点4
if (node.rightChild != null) {
return minElemNode(node.rightChild);}
// 若该结点右子树为空
TreeNode parentNode = node.parent;
while (parentNode != null && node == parentNode.rightChild) {
node = parentNode;
parentNode = parentNode.parent;}
return parentNode;
}
五.二叉搜索树的插入
先利用查找方法确定插入位置及方向,再将新节点作为叶子插入
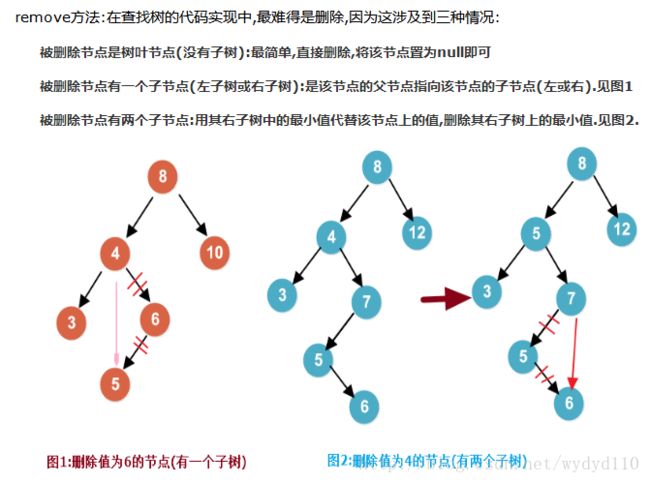
六.二叉搜索树的删除
参考:https://www.cnblogs.com/fingerboy/p/5493786.html