一、索引
高效获取数据数据结构。db设计者从查询算法角度进行优化
最基本查询算法:顺序查找(linear search),O(n)数据量很大时糟糕。更优秀查找算法,如:
二分查找(binary search):要求被检索数据有序
二叉树查找(binary tree search):只应用于二叉查找树上
数据不满足各种数据结构,所以,数据库维护满足特定查找算法数据结构,数据结构以某种方式引用(指向)数据,数据结构上实现高级查找算法。就是索引。
可能索引方式。左边是数据表,一共两列七条记录,最左边的是数据记录物理地址(注意逻辑上相邻的记录在磁盘上也并不是一定物理相邻的)。加快Col2查找,维护二叉查找树,每个节点分别包含索引键值和指向对应数据记录物理地址的指针,运用二叉查找O(log2n)的复杂度获取数据
实际数据库系统没有用二叉查找树或其进化品种红黑树(red-black tree)实现.
二、B-Tree和B+Tree
文件系统用B-Tree或其变种B+为索引结构
B-Tree
多路搜索树(并不是二叉的):
1.定义任意非叶子结点最多只有M个儿子;且M>2;
2.根结点的儿子数为[2, M];
3.除根结点以外的非叶子结点的儿子数为[M/2, M];
4.每个结点存放至少M/2-1(取上整)和至多M-1个关键字;(至少2个关键字)
5.非叶子结点的关键字个数=指向儿子的指针个数-1;
6.非叶子结点的关键字:K[1], K[2], …, K[M-1];且K[i] < K[i+1];
7.非叶子结点的指针:P[1], P[2], …, P[M];其中P[1]指向关键字小于K[1]的
子树,P[M]指向关键字大于K[M-1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])的子树;
8.所有叶子结点位于同一层;
9.每个k对应一个data。
如:(M=3)相当于一个2–3树,2–3树是一个这样的一棵树, 它的每个节点要么有2个孩子和1个数据元素,要么有3个孩子和2个数据元素,叶子节点没有孩子,并且有1个或2个数据元素。
(1)B-树的搜索
从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为空,或已经是叶子结点;B-Tree上查找算法的伪代码如下:
(2)B-树的特性:
1.关键字集合分布在整颗树中;
2.任何一个关键字出现且只出现在一个结点中;
3.搜索有可能在非叶子结点结束;
4.其搜索性能等价于在关键字全集内做一次二分查找;
5.自动层次控制;
(3)B-树的自控制:
B树中每一个内部节点会包含一定数量的键值。通常,键值的数量被选定在d和2d之间。在实际中,键值占用了节点中大部分的空间。因数2将保证节点可以被拆分或组合。如果一个内部节点有2d个键值,那么添加一个键值给此节点的过程,将会拆分2d键值为2个d键值的节点,并把此键值添加给父节点。每一个拆分的节点需要最小数目的键值。相似地,如果一个内部节点和他的邻居两者都有d个键值,那么将通过它与邻居的合并来删除一个键值。删除此键值将导致此节点拥有d-1个键值;与邻居的合并则加上d个键值,再加上从邻居节点的父节点移来的一个键值。结果为完全填充的2d个键值。
B-树的构造过程:
往B树中依次插入:
6 10 4 14 5 11 15 3 2 12 1 7 8 8 6 3 6 21 5 15 15 6 32 23 45 65 7 8 6 5 4
B+Tree
B-Tree变种,最常见的是B+Tree,MySQL就普遍使用B+Tree实现其索引结构。
(1)不同点:
1.非叶子结点的子树指针与关键字个数相同;
2.非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树(B-树是开区间);
3.为所有叶子结点增加一个链指针;
4.所有关键字都在叶子结点出现;
5.内节点不存储data,只存储key 如:(M=3)
B+的搜索与B-树也基本相同,区别是B+树只有达到叶子结点才命中(B-树可以在非叶子结点命中),性能也等价于在关键字全集做一次二分查找;
(2)B+的特性:
1.所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的;
2.不可能在非叶子结点命中;
3.非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层;
4.更适合文件索引系统;
B+树的构造过程:
下面是往B+树中依次插入
6 10 4 14 5 11 15 3 2 12 1 7 8 8 6 3 6 21 5 15 15 6 32 23 45 65 7 8 6 5 4
三、索引的物理存储
索引本身也很大,不可能全部存储在内存中,以索引文件的形式存储磁盘上。查找过程中就要产生磁盘I/O消耗,相对内存存取消耗要高几个数量级,评价索引的优劣指标,查找过程中磁盘I/O操作次数渐进复杂度。
每个盘块存放B树的结点(2个文件名)。一个BTNODE结点就代表一个盘块,子树指针存放另外一个盘块地址。
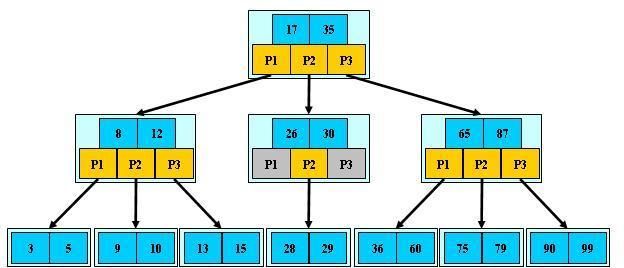
模拟查找文件29的过程:
1.根据根结点指针找到文件目录的根磁盘块1,将其中的信息导入内存。【磁盘IO操作 1次】
2.内存中两个文件名17、35和三个存储其他磁盘页面地址的数据。根据算法我们发现:17<29<35,因此我们找到指针p2。
3.根据p2指针,我们定位到磁盘块3,并将其中的信息导入内存。【磁盘IO操作 2次】
4.此时内存中有两个文件名26,30和三个存储其他磁盘页面地址数据。26<29<30找到指针p2。
5.定位到磁盘块8,将其中信息导入内存。【磁盘IO操作 3次】
6.内存中有28,29。找到29,定位了内存磁盘地址。
3次磁盘IO操作和3次内存查找操作。有序表结构,折半查找提高效率。IO操作是影响整个B树查找效率。
平衡二叉树:磁盘4次,最多5次,文件越多,B树比平衡二叉树所用的磁盘IO次数将越少,效率也越高。
B+tree
B+tree的优点:
1.磁盘读写代价更低
内部结点并没有指向关键字具体信息指针。内部结点相对B树更小。所有同一内部结点的关键字存放在同一盘块中,盘块容纳关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。IO读写次数也就降低了。
磁盘盘块容纳16bytes,关键字2bytes,关键字具体信息指针2bytes。
一棵9阶B-tree(一个结点最多8个关键字)内部结点:需要2个盘快。
B+树内部结点:内部结点读入内存中,只需要1个盘快。
2.查询效率更加稳定
非终结点并不是最终指向文件内容结点,叶子结点中关键字索引。关键字查找必须,走根结点到叶子结点的路。查询路径长度相同,查询效率相当。
四、mysql的两种存储引擎的索引存储机制
(1)MyISAM索引实现
B+Tree,叶节点data域存放数据记录地址。
表有三列,Col1为主键,索引文件仅仅保存数据记录地址。
Col2建立辅助索引:和主索引结构上没区别,
主索引要求key是唯一的,辅助索引的key可重复。
同样也是B+Tree,data域保存数据记录地址。MyISAM中索引检索算法,按B+Tree搜索算法搜索索引,指定Key存在,取其data域值,以data域的值为地址,读取相应数据记录。
索引方式“非聚集”
(2)InnoDB索引实现
用B+Tree,实现方式却与MyISAM截然不同。
(1)InnoDB的数据文件本身就是索引文件,索引key是主键。MyISAM索引文件(仅存地址)和数据文件是分离。InnoDB中,表数据文件本身按B+Tree组织的索引结构,叶节点data域存完整数据记录。。
InnoDB主索引(也是数据文件),(1)叶节点包含完整记录(聚集索引)。(2)数据文件按主键聚集,必须有主键(MyISAM可以没有),如没显式指定,自动选择可唯一标识数据记录列为主键,如不存在这种列,自动为InnoDB表生成隐含字段为主键,长度为6个字节长整形。
InnoDB辅助索引data域存储相应记录主键值而不是地址。定义Col3上辅助索引:
以英文字符的ASCII码作为比较准则。聚集索引这种实现方式使得按主键的搜索十分高效,但辅助索引搜索需要检索两遍索引:先检索辅助索引获得主键,然后用主键到主索引中检索获得记录。
知道InnoDB的索引实现,所有辅助索引都引用主索引,过长主索引会令辅助索引过大。例如,非单调字段为主键InnoDB中不是好主意,InnoDB数据文件本身是B+Tree,非单调的主键会造成在插入新记录时数据文件为了维持B+Tree的特性而频繁的分裂调整,十分低效,用自增字段为主键是好选择。
ps引用:
http://blog.codinglabs.org/articles/theory-of-mysql-index.html
http://blog.csdn.net/zhangliangzi/article/details/51367639
http://www.cnblogs.com/vincently/p/4526560.html
https://www.jianshu.com/p/1775b4ff123a