python递归の拾遗

递归 Recursion

在函数内部，可以调用其他函数。如果一个函数在内部调用自身本身，这个函数就是递归函数。

1、递归函数的执行过程

猜猜看执行结果：

def rec(n):
    n = int(n/2)      # 仅保留整数部分，5/2 --> 2 , 1/2 --> 0
    print(n)
    if n > 0:
         rec(n)
    print(n) 
rec(10)

输出：

5
2
1
0
0
1
2
5

执行逻辑顺序如下图：

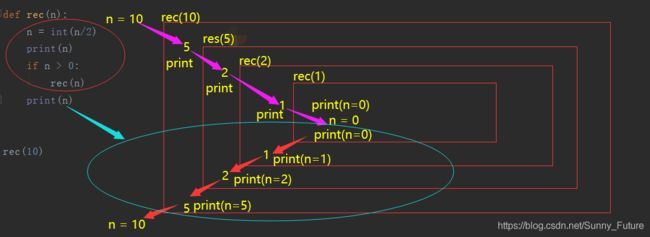
函数在每进入下一层的时候，当前层的函数并未结束，它必须等它调用的下一层函数执行结束返回后才能继续往下走。 所以最下面的那句print(n)会等最里层的函数执行时才会执行，然后不断往外退层，所以会出现0、1、2、5的效果。

2、递归的最大深度

2.1 查看最大深度

python为了我们程序的内存优化所设定的一个默认值 3000，最终的值根据计算机性能而定

In [41]: import sys

In [42]: sys.getrecursionlimit()
Out[42]: 3000

某台计算机实际能达到的递归深度

def foo(n):
    print(n)
    n += 1
    foo(n)
foo(1)

2.2 修改最大深度

这里将python允许的递归深度设置为了10w，至于实际可以达到的深度就取决于计算机的性能了，不过我们还是不推荐修改这个默认的递归深度，毕竟你的代码质量也很关键。。

# 修改默认最大深度
import sys
print(sys.setrecursionlimit(100000))

# 再次定义执行递归
def foo(n):
    print(n)
    n += 1
    foo(n)
foo(1)

修改之后，最大深度也是根据计算机性能而定，我这里最大到3221层

3、递归实现阶乘

阶乘的数学阶乘公式

n! = n x (n−1)! 
n! = n x (n−1) x (n−2)!
n! = n x (n−1) x (n−2) x (n−3)!
⋅
⋅
n! = n x (n−1) x (n−2) x (n−3) ⋅⋅⋅⋅ x 3!
n! = n x (n−1) x (n−2) x (n−3) ⋅⋅⋅⋅ x 3 x 2!
n! = n x (n−1) x (n−2) x (n−3) ⋅⋅⋅⋅ x 3 x 2 x 1!

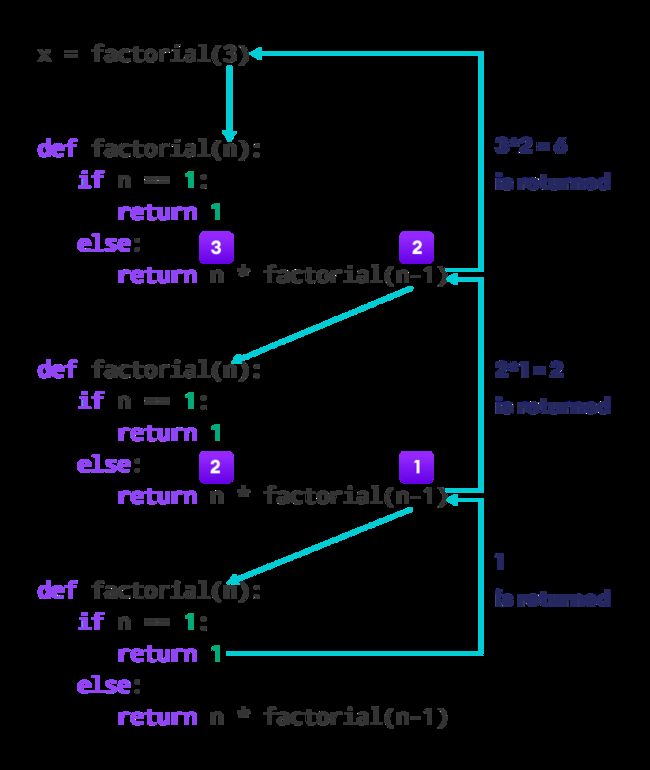
3.1 举例 3 的阶乘过程

递归函数实现如下

def factorial(x):
    """
    这是一个递归函数
    用于实现一个正整数的阶乘
    """
    if x == 1:
        return 1
    else:
        return x * factorial(x-1)


num = 3
print(num, "的阶乘是", factorial(num))

执行过程

factorial(3)          # 1st call with 3
3 * factorial(2)      # 2nd call with 2
3 * 2 * factorial(1)  # 3rd call with 1
3 * 2 * 1             # return from 3rd call as number=1
3 * 2                 # return from 2nd call
6                     # return from 1st call

3.2 再举例 5 的阶乘过程

递归函数实现如下

def factorial_recursive(n):
    # Base case: 1! = 1
    if n == 1:
        return 1

    # Recursive case: n! = n * (n-1)!
    else:
        return n * factorial_recursive(n-1)

输出：

>>> factorial_recursive(5)
120

3.3 递归特性

递归特性:

• 必须有一个明确的结束条件

• 每次进入更深一层递归时，问题规模相比上次递归都应有所减少

递归效率不高，递归层次过多会导致栈溢出（在计算机中，函数调用是通过栈（stack）这种数据结构实现的，每当进入一个函数调用，栈就会加一层栈帧，每当函数返回，栈就会减一层栈帧。由于栈的大小不是无限的，所以，递归调用的次数过多，会导致栈溢出）

3.4 二分法查找指定值

注意：二分查找法 要查找的序列必须是一个有序的序列

如题：l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]，找 66 的索引值

li = [100,2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
li.sort()
# [2, 3, 5, 10, 15, 16, 18, 22, 26, 30, 32, 35, 41, 42, 43, 55, 56, 66, 67, 69, 72, 76, 82, 83, 88, 100]


def binary_search(arr, x, start_index=0, end_index=0):
    end_index = end_index if end_index else len(arr) - 1
    if end_index > start_index:
        mid_index = start_index + ((end_index - start_index) // 2)                # 除 2 // 取整，且中间的索引值注意变化
        if x in arr and x > arr[mid_index]:
            return binary_search(arr, x, mid_index, end_index)
        elif x in arr and x < arr[mid_index]:
            return binary_search(arr, x, start_index, mid_index)
        elif x in arr and x == arr[mid_index]:
            return mid_index
        else:  # 假设已经取不到值了，在这种情况下，只能说明，要找的这个值 x 不在这个列表里
            return "Cannot find %s in this data list!" % x


res = binary_search(li, 66)
print(res)

3.5 递归实现三级菜单

通过递归实现三级菜单，需求是 按 b 逐层退出，按 q 直接退出程序。
注意：函数在每进入下一层的时候，当前层的函数并未结束，它必须等它调用的下一层函数执行结束返回后才能继续往下走。----->以此实现 按b 返回上级菜单

# 菜单内容
menu_addr = {
    '北京': {
        '海淀': {
            '五道口': {
                'soho': {},
                '网易': {},
                'google': {}
            },
            '中关村': {
                '爱奇艺': {},
                '汽车之家': {},
                'youku': {},
            },
            '上地': {
                '百度': {},
            },
        },
        '昌平': {
            '沙河': {
                '老男孩': {},
                '北航': {},
            },
            '天通苑': {},
            '回龙观': {},
        },
        '朝阳': {},
        '东城': {},
    },
    '上海': {
        '闵行': {
            "人民广场": {
                '炸鸡店': {}
            }
        },
        '闸北': {
            '火车战': {
                '携程': {}
            }
        },
        '浦东': {},
    },
    '山东': {},
}

#  首先明确递归： 有递  肯定也有归！其次 判断 逐次返回传值的情况，
#  这里若key是q，那么逐层返回q并释放内存空间，再输入 key 遍历执行三级菜单函数

def three_level_menu(menu):
    while True:
        for key in menu: print(key)
        key = input('请输入选项【b(返回上级)|q(退出程序)】：').strip()
        if key in menu:
            res = three_level_menu(menu[key])
            if res == 'q':
                return 'q'
        if key == 'q':
            return 'q'
        if key == 'b':
            return


three_level_menu(menu_addr)

3、总结

• 不能无限次数的递归 3000
• 在一个函数的内部调用这个函数本身
• 停止一次递归的方法就是让递归内层函数return（包括return None）