多维缩放（Multiple Dimensional Scaling）MDS-机器学习

多维缩放（Multiple Dimensional Scaling）MDS机器学习matlab实战

1算法目的

一般的数据是高维的，但是与学习任务相关的一般是某个低维度的分布，即一个低维的嵌入。
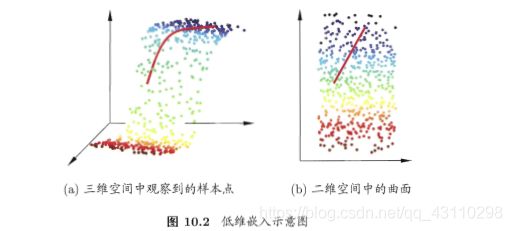如上图所示

2 算法推导

• 算法的原则是：原始空间中样本之间的距离在低维度能够保持
• 算法的目标：获得样本在低维度空间的坐标，且两个任意样本在低维度空间的欧式距离等于原始空间的距离。

具体的算法推导可以看看其他的博客，很多都说的很好，在此不多说。

3 算法实现

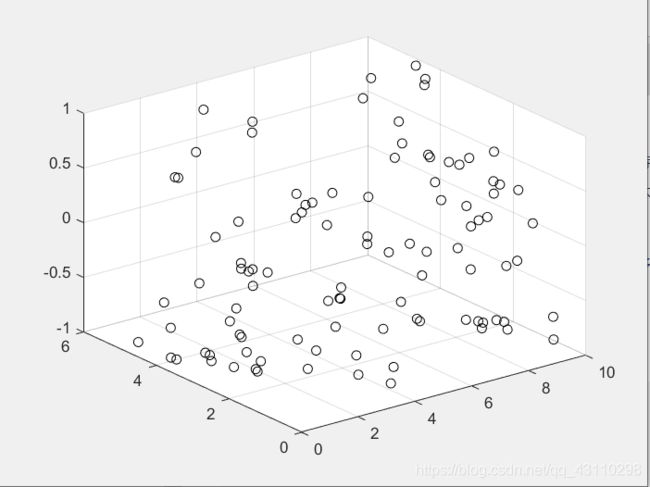
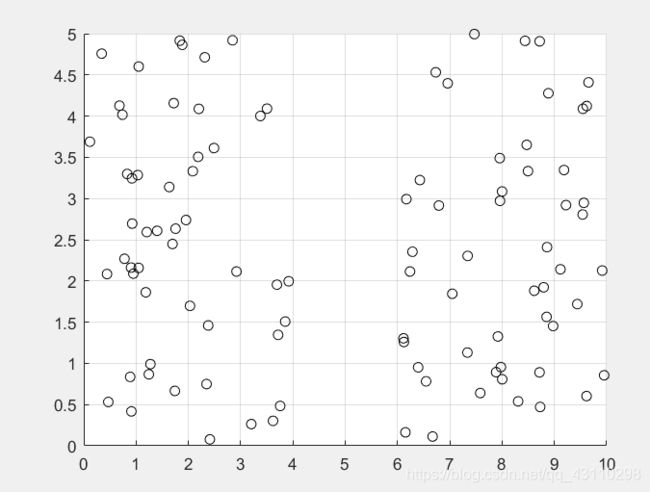
1. 首先生成一系列的点

clear;
clc;
a = 10; %%%%% 长
b = 5; %%%%% 宽
n = 100; %%%%% 点数量
% cxd1 = a*rand(n,1); %%%%%% 产生横坐标0-10
cxd11=4*rand(50,1);  %0-4范围内随产生点
cxd12=6+4*rand(n-50,1);%6-10范围内随机产生点
cxd1=[cxd11;cxd12];
cxd2 = b*rand(n,1); %%%%%% 产生纵坐标
cxd = [cxd1 cxd2]; %%%%%% 生产随机点
z=sin(cxd(:,1)+cxd(:,2));
scatter3(cxd1,cxd2,z,'k'); 

看似无规律，但是如果换个角度

其实是一个正弦函数。

再换个角度：（从上往下看）

fig2

然后我们使用MDS进行降维，同时保证：

• 降维前后两点的欧式距离不变
  完整代码

clear;
clc;
a = 10; %%%%% 长
b = 5; %%%%% 宽
n = 100; %%%%% 点数量
% cxd1 = a*rand(n,1); %%%%%% 产生横坐标0-10
cxd11=4*rand(50,1);  %0-4范围内随产生点
cxd12=6+4*rand(n-50,1);%6-10范围内随机产生点
cxd1=[cxd11;cxd12];
cxd2 = b*rand(n,1); %%%%%% 产生纵坐标
cxd = [cxd1 cxd2]; %%%%%% 生产随机点
z=sin(cxd(:,1)+cxd(:,2));
scatter3(cxd1,cxd2,z,'k'); 
dist = zeros(n,n);
for i =1:n
    for j =1:n
        a = cxd(i,:); b=cxd(j,:);
        dist(i,j)=sqrt((a-b)*(a-b)');
    end
end
m=n;
DSquare=dist.^2;
for i = 1:m
    DSquare_j(i) = 1/m*sum(DSquare(i,:));
end
%求各列的和
for j = 1:size(DSquare,1)
    DSquare_i(j) = 1/m*sum(DSquare(:,j));
end
%求矩阵的总和
DSquare_ij = 1/m^2*sum(sum(DSquare(:,:)));
%求内积矩阵
for i = 1:m
    for j = 1:m
        B(i,j) = -1/2*(DSquare(i,j) - DSquare_j(i) - DSquare_i(j) + DSquare_ij);
    end
end
 % 特征值分解,保留最大的值
 [V,D] = lun6(B,2);
 % 把D转化为对角阵
 D = diag(D);
 Z=D.^0.5*V';
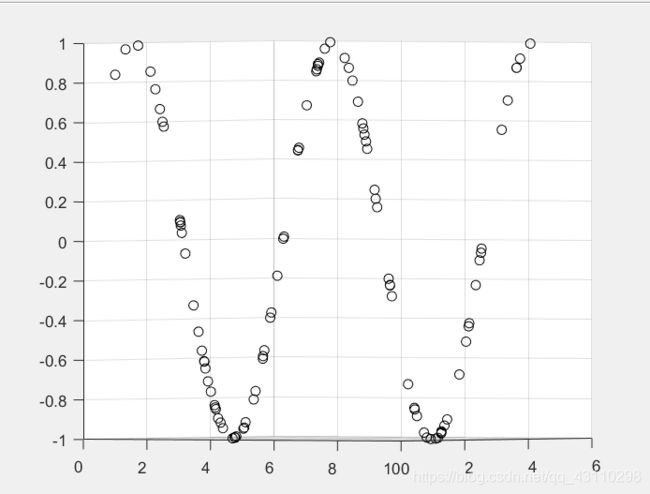
 figure(2)
 plot(Z(1,:),Z(2,:),'o');

其中lun6函数如下（保留最大的几个特征值及其特征向量）

function [v,d] = lun6(A, k)

if nargin == 0
    A = [1 3 7;3 8 9;5 4 6];
    k = 2;
end
[V, D] = eig(A);
D = diag(D);
[D, I] = sort(D, 'descend');
if k > length(D)
    k = length(D);
end
d = D(1 : k);
v = V(:, I(1 : k));

最后结果：从三维到二维，将原来的三维的数据映射到二维中去

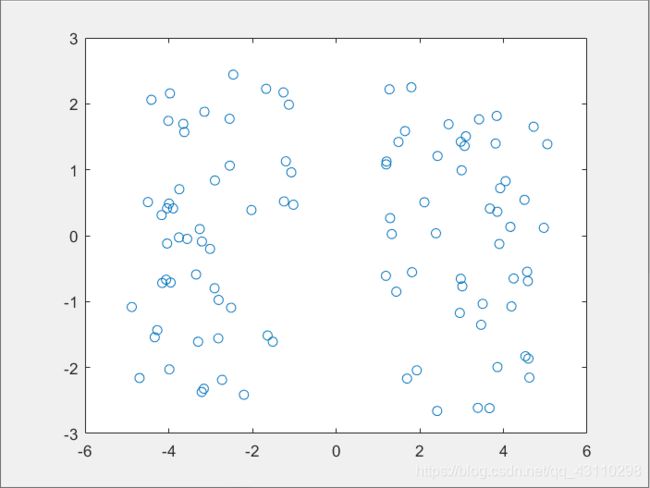
fig3

这样就完成了MDS，并且保留的原本的欧式距离同时完成降维。
这样做的意义在哪里呢？在欧式空间中计算的离散度未必有用，而在展开后的平面内却有用。

---

2020年3月20日更新

1 三维马鞍面–>MDS–>降维

%%%%%%程序目录
% %% 画马鞍面
% %% 使用PCA进行降维
% %% 判断降维效果
% %% 使用MDS
% %% 判断降维效果
%%%%%%%


%% 画马鞍面
clc;clear;close all;
x=-5:0.5:5;
y=-5:0.5:5;
% 加入噪声
x = x + 0.2*rand(1,length(x));
y = y + 0.2*rand(1,length(x));
[X,Y]=meshgrid(x,y); %确定作图的范围
X = X + rand(length(x),length(y));
Y = Y + rand(length(x),length(y));
Z=X.^2-Y.^2+0.1*rand(length(x),length(y)); %一定要加 '.' 号，因为X、Y是矩阵
C = X+Y;
% axis equal
% surf(X,Z,Y,C)
x1 = reshape(X,[],1);
y1 = reshape(Y,[],1);
z1 = reshape(Z,[],1);
c1 = reshape(C,[],1);
data_pca = [x1,y1,z1];
% 画图
figure(1)
axis equal
scatter3(x1,y1,z1,5,c1)
%% 使用PCA进行降维
[pc,scores] = pcaa(data_pca,2);
figure(2)
axis equal
scatter(pc(:,1),pc(:,2),5,c1)
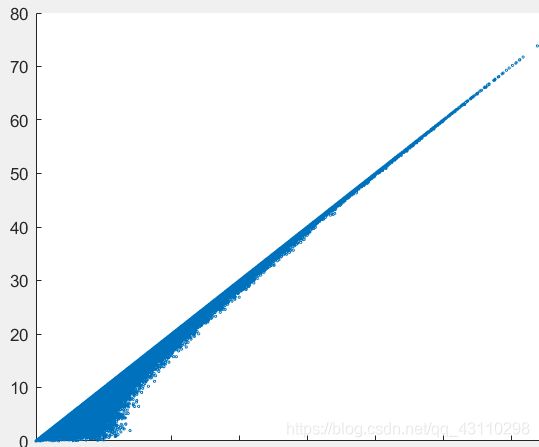
%% 判断降维效果
% 计算原距离
x_dis = L2_distance(data_pca',data_pca');
y_dis = L2_distance(pc',pc');
x_re_dis = reshape(x_dis,1,[]);
y_re_dis = reshape(y_dis,1,[]);
scatter(x_re_dis,y_re_dis,2)
%% 使用MDS
new_MDS = MDS(data_pca,3);
scatter3(new_MDS(1,:),new_MDS(2,:),new_MDS(3,:),5,c1)
%% 判断降维效果
% 计算原距离
x_dis = L2_distance(data_pca',data_pca');
y_dis = L2_distance(new_MDS,new_MDS);
x_re_dis = reshape(x_dis,1,[]);
y_re_dis = reshape(y_dis,1,[]);
scatter(x_re_dis,y_re_dis,2)

原本比较平滑的马鞍面


结果被弯曲成了这样，而对于二维：更差劲，或许只是看上去不好

判断一下效果，看来局部距离的差距较大，而远处的效果较好。当然，当降维到3为的时候，是可以完全满足：和原来的欧式空间的距离相同的条件。