Python处理图像—将笛卡尔坐标系转换为极坐标系
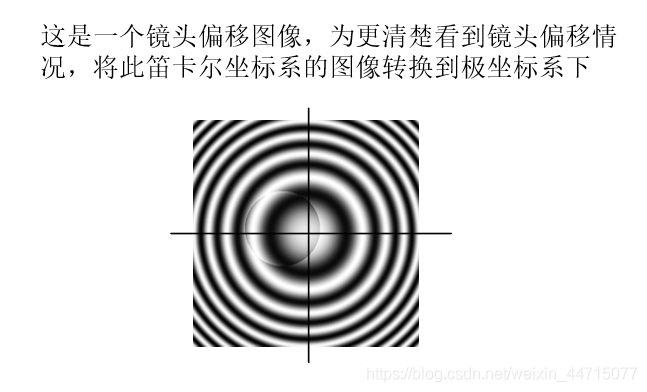
首先讲一下思路:
根据想要输出的目标图像划分好矩阵再去用插值算法寻找原图的像素值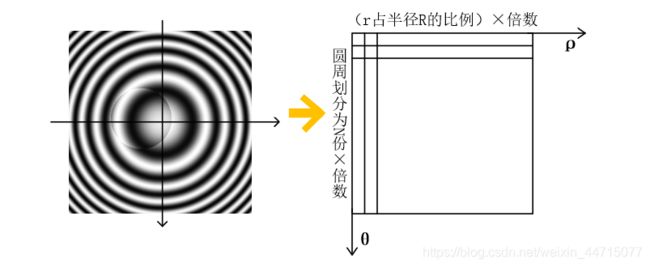
import matplotlib.pyplot as plt
import numpy as np
from skimage import io,color,morphology,transform
import math
img = io.imread('uu.png',as_gray=True)#矩阵形式
M ,N = img.shape
index = M if M<N else N
R_r = int(input("请输入大于{}的数字>>>".format(index)))
R_t = int(input("请输入大于360的数字>>>"))
x_0 = np.int_(np.floor(M/2))
y_0 = np.int_(np.floor(N/2))
d_t = 360/R_t #划分圆周
d_r = index/R_r #划分半径
class Conversion:
PI = np.pi
dst = np.zeros((R_r, R_t), dtype=float)
def __init__(self,R_r=R_r ,R_t = R_t,x_0 = x_0,y_0 = y_0,d_t = d_t,d_r = d_r,img=img):
self.img = img
self.R_r = R_r
self.R_t = R_t
self.x_0 = x_0
self.y_0 = y_0
self.d_t = d_t
self.d_r = d_r
#双线性
def interpolate_bilinear(self,ri, rf, rc, yi, yf, yc):
if yf == yc & rc == rf:
out = img[yc][rc]
elif yf == yc:
out = (ri - rf) * img[yf][rc] + (rc - ri) * img[yf][rf]
elif rf == rc:
out = (yi - yf) * img[yc][rf] + (yc - yi) * img[yf][rf]
else:
inter_r1 = (ri - rf) * img[yf][rc] + (rc - ri) * img[yf][rf]
inter_r2 = (ri - rf) * img[yc][rc] + (rc - ri) * img[yc][rf]
out = (yi - yf) * inter_r2 + (yc - yi) * inter_r1
return out
#最邻近
def interpolate_adjacent(self,ri, rf, rc, yi, yf, yc):
r = 0
if (ri - rf) > (rc - ri):
r = rc
else:
r = rf
if (yi - yf) > (yc - yi):
if yc >= M:
y = M - 1
else:
y = yc
else:
if yf >= M:
y = M - 1
else:
y = yf
out = img[y][r]
return out
def cal(self):
for i in range(R_r):
for y in range(R_t):
print(i, y)
if i == 0:
Conversion.dst[i][y] = img[x_0][y_0]
elif y >= 0 & y < (R_t / 4):
self.condition_1(i,y)
elif y >= R_t / 4 & y < (R_t / 2):
self.condition_2(i,y)
elif y >= (R_t / 2) & y < (R_t * 3 / 4):
self.condition_3(i,y)
elif y >= (R_t * 3 / 4) & y <= R_t:
self.condition_4(i,y)
def condition_1(self,i,y):
xi = np.sqrt(np.power(i * d_r, 2) / (1 + np.power(np.tan(y * d_t / 180 * Conversion.PI), 2))) + x_0
xf = np.int_(np.floor(xi))
xc = np.int_(np.ceil(xi))
yi = np.sqrt((np.power(i * d_r, 2) * np.power(np.tan(y * d_t / 180 * Conversion.PI), 2)) / (
1 + np.power(np.tan(y * d_t / 180 * Conversion.PI), 2))) + y_0
yf = np.int_(np.floor(yi))
yc = np.int_(np.ceil(yi))
# dst[i][y] = self.interpolate_adjacent(xi,xf,xc,yi,yf,yc)
Conversion.dst[i][y] = self.interpolate_bilinear(xi, xf, xc, yi, yf, yc)
def condition_2(self,i,y):
xi = abs(np.sqrt(np.power(i * d_r, 2) / (1 + np.power(np.tan(y * d_t / 180 * Conversion.PI), 2))) - x_0)
xf = np.int_(np.floor(xi))
xc = np.int_(np.ceil(xi))
yi = np.sqrt((np.power(i * d_r, 2) * np.power(np.tan(*d_t * Conversion.PI), 2)) / (
1 + np.power(np.tan(y * d_t / 180 * Conversion.PI), 2))) + y_0
yf = np.int_(np.floor(yi))
yc = np.int_(np.ceil(yi))
# dst[i][y] = interpolate_adjacent(xi, xf, xc, yi, yf, yc)
Conversion.dst[i][y] = self.interpolate_bilinear(xi, xf, xc, yi, yf, yc)
def condition_3(self,i,y):
xi = abs(np.sqrt(np.power(i * d_r, 2) / (1 + np.power(np.tan(y * d_t / 180 * Conversion.PI), 2))) - x_0)
xf = np.int_(np.floor(xi))
xc = np.int_(np.ceil(xi))
yi = abs(np.sqrt((np.power(i * d_r, 2) * np.power(np.tan(y * d_t / 180 * Conversion.PI), 2)) / (
1 + np.power(np.tan(y * d_t / 180 * Conversion.PI), 2))) - y_0)
yf = np.int_(np.floor(yi))
yc = np.int_(np.ceil(yi))
# dst[i][y] = self.interpolate_adjacent(xi, xf, xc, yi, yf, yc)
Conversion.dst[i][y] = self.interpolate_bilinear(xi, xf, xc, yi, yf, yc)
def condition_4(self,i,y):
xi = np.sqrt(np.power(i * d_r, 2) / (1 + np.power(np.tan(y * d_t / 180 * Conversion.PI), 2))) + x_0
xf = np.int_(np.floor(xi))
xc = np.int_(np.ceil(xi))
yi = abs(np.sqrt((np.power(i * d_r, 2) * np.power(np.tan(y * d_t / 180 * Conversion.PI), 2)) / (
1 + np.power(np.tan(y * d_t / 180 * Conversion.PI), 2))) - y_0)
yf = np.int_(np.floor(yi))
yc = np.int_(np.ceil(yi))
# dst[i][y] = self.interpolate_adjacent(xi, xf, xc, yi, yf, yc)
Conversion.dst[i][y] = self.interpolate_bilinear(xi, xf, xc, yi, yf, yc)
p = Conversion()
p.cal()
img_gray= color.rgb2gray(p.dst)
plt.imshow(p.dst,cmap='gray')
plt.show()
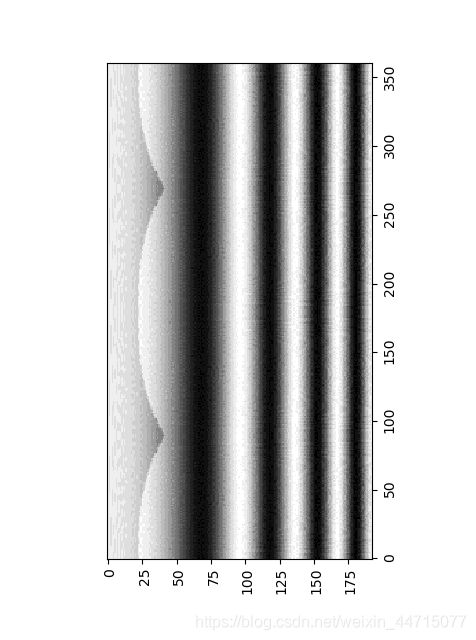
看一下结果:
分享知识,造福人民,为实现我们中华民族伟大复兴!祝大家越来越好!


