LeNet-5

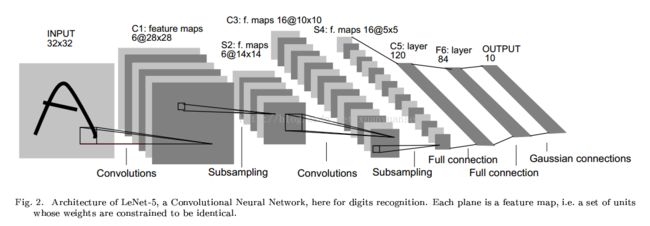
LeNet-5是一个较简单的卷积神经网络。下图显示了其结构：输入的二维图像，先经过两次卷积层到池化层，再经过全连接层，最后使用softmax分类作为输出层

 

模型结构:

LeNet-5共有7层（不包含输入层），每层都包含可训练参数；每个层有多个Feature Map，每个FeatureMap通过一种卷积滤波器提取输入的一种特征，然后每个FeatureMap有多个神经元。

　　C1层是一个卷积层
　　输入图片：32 * 32
　　卷积核大小：5 * 5 卷积核种类：6
　　输出featuremap大小：28 * 28 （32-5+1）
　　神经元数量：28 * 28 * 6
　　可训练参数：（5 * 5+1） * 6（每个滤波器5 * 5=25个unit参数和一个bias参数，一共6个滤波器）
　　连接数：（5 * 5+1） * 6 * 28 * 28

 

　　S2层是一个下采样层

　　输入：28 * 28
　　采样区域：2 * 2
　　采样方式：4个输入相加，乘以一个可训练参数，再加上一个可训练偏置。结果通过sigmoid
　　采样种类：6
　　输出featureMap大小：14 * 14（28/2）
　　神经元数量：14 * 14 * 6
　　可训练参数：2 * 6（和的权+偏置）
　　连接数：（2 * 2+1） * 6 * 14 * 14
　　S2中每个特征图的大小是C1中特征图大小的1/4

　　C3层也是一个卷积层
　　输入：S2中所有6个或者几个特征map组合
　　卷积核大小：5 * 5
　　卷积核种类：16
　　输出featureMap大小：10 * 10
　　C3中的每个特征map是连接到S2中的所有6个或者几个特征map的，表示本层的特征map是上一层提取到的特征map的不同组合
　　存在的一个方式是：C3的前6个特征图以S2中3个相邻的特征图子集为输入。接下来6个特征图以S2中4个相邻特征图子集为输入。然后的3个以不相邻的4个特征图子集为输入。　　最后一个将S2中所有特征图为输入。 则：可训练参数：6 * （3 * 25+1）+6 * （4 * 25+1）+3 * （4 * 25+1）+（25 * 6+1）=1516
　　连接数：10 * 10 * 1516=151600

 

　　S4层是一个下采样层
　　输入：10 * 10
　　采样区域：2 * 2
　　采样方式：4个输入相加，乘以一个可训练参数，再加上一个可训练偏置。结果通过sigmoid
　　采样种类：16
　　输出featureMap大小：5 * 5（10/2）
　　神经元数量：5 * 5 * 16=400
　　可训练参数：2 * 16=32（和的权+偏置）
　　连接数：16 * （2 * 2+1） * 5 * 5=2000
　　S4中每个特征图的大小是C3中特征图大小的1/4

　　C5层是一个卷积层
　　输入：S4层的全部16个单元特征map（与s4全相连）
　　卷积核大小：5 * 5 卷积核种类：120
　　输出featureMap大小：1 * 1（5-5+1）
　　可训练参数/连接：120 * （16 * 5 * 5+1）=48120

　　F6层全连接层
　　输入：c5 120维向量
　　计算方式：计算输入向量和权重向量之间的点积，再加上一个偏置，结果通过sigmoid函数
　　可训练参数:84 * (120+1)=10164

模型特性:

• 卷积网络使用一个3层的序列：卷积、池化、非线性——这可能是自这篇论文以来面向图像的深度学习的关键特性！
• 使用卷积提取空间特征
• 使用映射的空间均值进行降采样
• tanh或sigmoids非线性
• 多层神经网络（MLP）作为最终的分类器
• 层间的稀疏连接矩阵以避免巨大的计算开销

 

import tensorflow.examples.tutorials.mnist.input_data as input_data
import tensorflow as tf

mnist = input_data.read_data_sets('MNIST_data', one_hot=True)


def compute_accuracy(v_xs,v_ys):
    global prediction
    y_pre = sess.run(prediction,feed_dict={xs:v_xs})
    correct_prediction = tf.equal(tf.argmax(y_pre,1),tf.argmax(v_ys,1))
    accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32))
    result = sess.run(accuracy,feed_dict={xs:v_xs,ys:v_ys})

    return result
xs = tf.placeholder(tf.float32,[None,784])
ys = tf.placeholder(tf.float32,[None,10])

x_image = tf.reshape(xs,[-1,28,28,1])

def weights(shape):
    weight = tf.truncated_normal(shape,stddev=0.1)
    return tf.Variable(weight)

def biases(shape):
    bias = tf.constant(0.1,shape=shape)
    return tf.Variable(bias)

def conv2d(x,W):
    return tf.nn.conv2d(input=x,filter=W,strides=[1,1,1,1],padding='SAME')

def max_pool_2x2(x):
    return tf.nn.max_pool(x,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')

# 1st layer: conv+relu+max_pool
w_conv1 = weights([5,5,1,6])
b_conv1 = biases([6])
h_conv1 = tf.nn.relu(conv2d(x_image,w_conv1)+b_conv1)
h_pool1 = max_pool_2x2(h_conv1)

# 2nd layer: conv+relu+max_pool
w_conv2 = weights([5,5,6,16])
b_conv2 = biases([16])
h_conv2 = tf.nn.relu(conv2d(h_pool1, w_conv2)+b_conv2)
h_pool2 = max_pool_2x2(h_conv2)
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*16])

# 3rd layer: 3*full connection
w_fc1 = weights([7*7*16,120])
b_fc1 = biases([120])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat,w_fc1)+b_fc1)

w_fc2 = weights([120, 84])
b_fc2 = biases([84])
h_fc2 = tf.nn.relu(tf.matmul(h_fc1, w_fc2)+b_fc2)

w_fc3 = weights([84, 10])
b_fc3 = biases([10])
prediction = tf.nn.softmax(tf.matmul(h_fc2, w_fc3)+b_fc3)

cross_entropy = tf.reduce_mean(-tf.reduce_sum(ys*tf.log(prediction),reduction_indices=[1]))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)



with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())

    for i in range(2000):
        batch_xs, batch_ys = mnist.train.next_batch(100)
        sess.run(train_step, feed_dict={xs: batch_xs, ys: batch_ys})
        if i % 100 == 0:
            print(compute_accuracy(mnist.test.images, mnist.test.labels))

 

 

转载于:https://www.cnblogs.com/lijie-blog/p/10165641.html