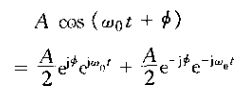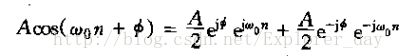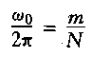《信号与系统学习笔记》—信号与系统(二)
注:本博客是基于奥本海姆的《信号与系统》第二版编写,主要是为了自己学习的复习与加深。
一、指数信号与正弦信号
一)、连续时间复指数信号与正弦信号
1、连续时间复指数信号具有如下形式:
其中C和a一般为复数。根据这些参数值的不同,复指数信号可有几种不同的特征。
2、实指数信号
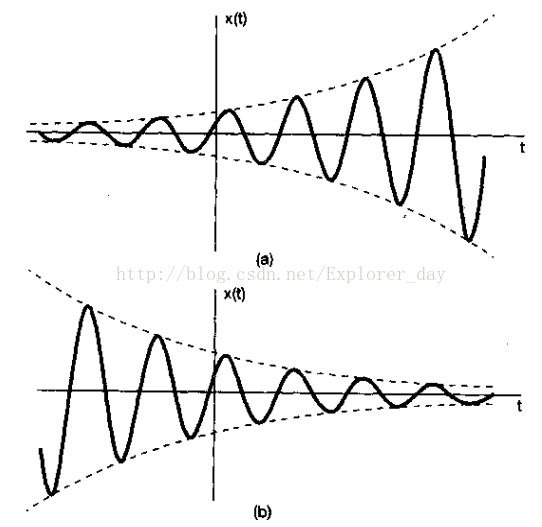
如上图所示,若C和a都是实数,这时的x(t)称为实指数信号,具有两种类型的特征:
1)、若a实正数,那么x(t)随t的增加而呈指数增长。
2)、若a实复数,则x(t)随t的增加而呈现指数衰减。
3、周期复指数
第二种重要的复指数是将a限制为纯虚函数。特别考虑一下函数
该信号的一个重要性质是,他是周期信号。
4、正弦信号
与周期复指数信号密切相关的一种信号是正弦信号
5、复指数信号与正弦信号的转换(欧拉公式)
1)、利用欧拉公式,副指数信号可以用预期相同基波周期的正弦信号来表示,即
2)、而正弦信号也能用相同基波周期的复指数信号来表示,即
注意:上面的式子中的两个指数信号都有复数振幅,所以正弦信号还可以用复指数信号表示为:
其中,若c是一个复数,则Re{c}记为它的实部。Im{c}记为它的虚部,即
6、基波频率
连续时间正弦信号或一个周期复指数信号,其基波周期T0是与|w0|成反比的,也称w0的基波频率。
7、周期信号,尤其是复指数信号和正弦信号,给出了具有无限能量弹有有限平均功率的此类信号的例子。
8、周期复指数信号在讨论信号与系统的大部分问题都起着十分重要的作用,部分原因是由于对许多其他信号来说,它们可用来作为极其有用的信号基本构造单元。
同时,一组成谐波关系的复指数信号也是很有用的,也就是说,周期复指数信号的集合内的全部信号都是周期的,且有一个公共周期T0.具体而言,对一个复指数信号,要成为
具有周期为T0的周期信号的必要条件是:
这就意味着wT0是2π的倍数,即
由此,若定义
则一个城谐波关系的复指数信号的集合就是一组其基波频率是某一正频率w0的整数倍的周期复指数信号,即
若k=0,其就是一个常数;而对任何其他的k值,其实周期的,其基波频率为|k|w0,级波周期为
9、一般复指数信号
最一般的情况下的复指数信号可以借助于已经讨论过的实指数信号和周期复指数信号来表示和说明。
利用欧拉关系,可以进一步展开为
由此可见:
1)、若r=0,则负指数信号的实部和虚部都是正弦的。
2)、若r>0,其实部和虚部则是一个振幅呈指数增长的正弦信号。
3)、若r<0,则为振幅呈指数衰减的正弦信号。
如下图所示
二)、离散时间复指数信号与正弦信号
1、与连续时间情况一样,一种重要的离散时间信号时复指数信号或序列,定义为
其中C和a一般均为复数。若令a=ep,择优另一种表示形式为
2、实指数信号
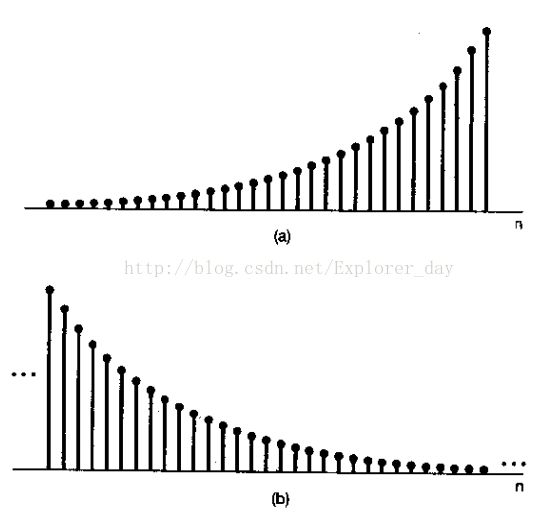
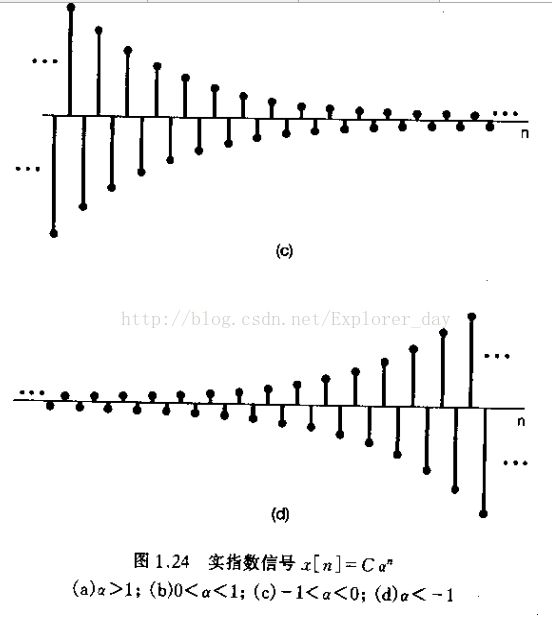
如果C和a都是实数,name就会有下图几种特性
1)、若|a|>1,则信号随n呈指数增长。
2)、若|a|<1,则信号随n呈指数衰减。若a是正值,则Can的所有值都具有同一符号。而若a是负值,则x[n]的符号交替变化。
3)、若a=1,则Can的所有值都具有同一符号。
4)、若a=-1,x[n]的值就在+C和-C之间交替变化。
3、正弦信号
如果将p局限于纯虚数,即|a|=1,就可以得到另一个重要的复指数序列。具体而言,考虑如下序列
入连续时间信号一样,此信号是与正弦信号密切相关的,即
4、欧拉公式
利用欧拉公式可以将复指数和正弦序列联系起来为
以及
5、一般复指数信号
一般离散时间复指数信号可以用实指数和正弦信号来表示。具体而言,将C和a均以极坐标给出,即
以及
则有
1)、对|a|=1,复指数序列的实部和虚部都是正弦序列。
2)、对|a|<1,其实部和虚部为正弦序列乘以一个呈指数衰减的序列。
3)、对|a|>1,则乘以一个呈指数增长的序列。
如下图所示
三)、离散时间复指数序列的周期性质
1、虽然连续时间时间和离散时间信号之间有许多相似之处,但是也存在一些重要的差别,其中之一是关于离散时间指数信号ejw0n的。
1)、w0越大,信号震荡的速率就越高。
2)、ejw0t对任何w0值都是周期的。
2、离散时间和连续时间不同
1)、第一个性质,研究频率为w0+2π的离散时间复指数信号:
上式表明,离散时间复指数信号在频率w0+2π与w0时是完全一样的。这一点与连续时间复指数信号ehw0t完全不同,后者不同的w0就对应着不同的信号,而在离散时间
情况下,具有频率为w0的复指数信号与w0+2π,w0+4π,.....等等这些频率的复指数信号则是一样的。
2)、第二个性质是关于离散时间复指数信号的周期问题。为了使信号ejw0n使周期的,周期为N>0,就必须
这就等效于要求
为了使上式成立,w0N必须是2π的整数倍,也就是说必须有一个整数m,满足
或者
根据上式,若w0/2π是一个有理数,ejw0n就是周期的,否则就不是周期的。
3、离散时间复指数信号的基波周期和基波频率
1)、基波频率
2)、基波周期
4、信号ejw0t和ejw0n的比较
5、组成谐波关系的周期离散时间复指数信号在离散时间与系统分析中也是有很大的价值的。这就是一组具有公共周期N的周期复指数信号,这些信号的频率都是基波频率
2π/N的整数倍,即
在连续时间情况下,这些呈谐波关系的信号![]() ,....都是互不相同的。然而,在离散时间情况下却不是这样的,因为
,....都是互不相同的。然而,在离散时间情况下却不是这样的,因为
这意味着,式子1.6所给出的一组信号中,仅有N个互不相同的周期复指数信号。