论文阅读“Cooperative Service Caching and Workload Scheduling in Mobile Edge Computing”

原文地址：https://arxiv.org/pdf/2002.01358

Abstract

移动边缘计算通过将云功能推到网络边缘，有利于减少服务响应时间和核心网络流量。拥有存储和计算能力的边缘节点可以缓存资源密集型和延迟敏感的移动应用程序的服务，并处理相应的计算任务，而不需要外包给中心云。但是，由于边缘资源容量的异构性和边缘存储计算能力的不一致性，使得边缘节点之间没有协作的情况下，很难共同充分利用存储计算能力。为了解决这个问题，我们考虑了边缘节点之间的协作，并研究了移动边缘计算中的协作服务缓存和工作负载调度。该问题可表示为具有非多项式计算复杂度的混合整数非线性规划问题。为了克服子问题耦合、计算通信折衷和边缘节点异构等问题，我们开发了一个迭代算法ICE。该算法是基于 Gibbs sampling和 water filling的思想设计的，Gibbs sampling采样的结果被证明是接近最优的，而water filling的计算复杂度是多项式的。仿真结果表明，与基准算法相比，我们的算法可以共同减少服务响应时间和外包流量。

I. INTRODUCTION

移动设备的普及和物联网的发展，推动了目标识别、增强现实、移动游戏等资源密集型、时延敏感的移动应用的出现。移动云计算提出将这些应用卸载到中心云，但中心云存在广域网延迟失控的问题，难以保证对延迟敏感的应用的服务质量 [1]– [3].另外，根据Cisco的预测，到2021年[4]，需要处理的移动数据的增长率将远远超过中心云的容量。将外包流量限制在中心云成为网络运营商关注的关键问题。移动边缘计算已经成为解决上述[5]、[6]问题的一个有前途的解决方案。移动边缘计算的典型形式是通过分布式部署存储和计算能力，赋予移动基站(也称为边缘节点) cloud-like功能。通过在边缘节点缓存移动应用程序的服务(包括程序代码和相关数据库)，移动边缘计算能够在网络边缘处理相应的计算任务，从而减少了服务响应时间，并将流量外包到中心云。

与具有弹性资源能力的移动云计算相比，移动边缘计算的主要局限性是边缘节点的资源能力有限。当边缘节点之间没有协作时，边缘资源的能力容易被利用不足，原因有二。首先，边缘资源能力的异质性会导致资源利用不足。对于存储容量不足以缓存服务或无法为应用程序提供足够计算能力的边缘节点，必须将相应的计算任务外包给中心云而不是附近强大的边缘节点，导致边缘资源[7]的利用率不足。此外，边缘节点存储和计算能力的不一致进一步加剧了边缘资源的浪费。具有较大计算能力的边缘节点如果没有足够的存储容量来缓存服务，就无法处理大量的计算任务，从而导致边缘计算能力的利用率不足。为了充分利用边缘节点的存储和计算能力，探索边缘节点之间的协作潜力至关重要。

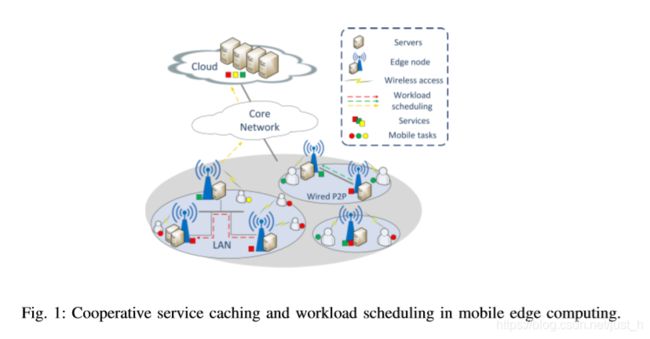
本文考虑了边缘节点间的协作，研究了移动边缘计算中的协作服务缓存和工作负载调度问题。如图1所示，附近的边缘节点通过局域网或有线点对点连接[8]进行连接。对于没有缓存服务或没有提供足够计算能力的边缘节点，可以将相应的计算任务转移到附近未充分利用的边缘节点，这些边缘节点缓存了服务或将其外包给云。通过利用边缘节点间的协作，可以充分利用异构的边缘资源容量，缓解单个边缘节点资源容量的不一致性。现有的工作考虑了边缘合作，并联合优化了服务缓存和工作负载调度，试图在确保服务缓存成本在预算[9]、[10]范围内的同时，最大化边缘节点服务的总体请求。然而，在实际情况中很难确定预算的确切价值。此外，虽然减少延迟是移动边缘计算的主要优势，但是现有的工作中并没有将服务响应时间作为性能标准。在本文中，我们研究了以最小化服务响应时间和外包流量为目标的协同服务缓存和工作负载调度(记为问题1)。

解决这个问题有三个方面的挑战。首先，服务缓存和工作负载调度是耦合的。服务缓存策略确定工作负载调度的决策空间，反过来，工作负载调度结果反映服务缓存策略的性能。解决问题1需要考虑两个子问题之间的相互作用。其次，最小化服务响应时间需要适当地平衡计算和传输延迟。虽然将计算任务从超载的边缘节点转移到附近未充分利用的边缘节点有利于减少计算延迟，但任务转移会导致局域网上额外的传输延迟。最优解决问题1应该处理计算-通信的权衡。第三，解决问题1需要处理边缘资源容量的异质性。边缘节点在存储和计算能力上是异构的。优化问题1需要平衡异构边缘节点之间的工作负载，导致计算复杂度呈指数增长。如何处理边缘异构问题，设计计算复杂度较低的算法是一个难题。

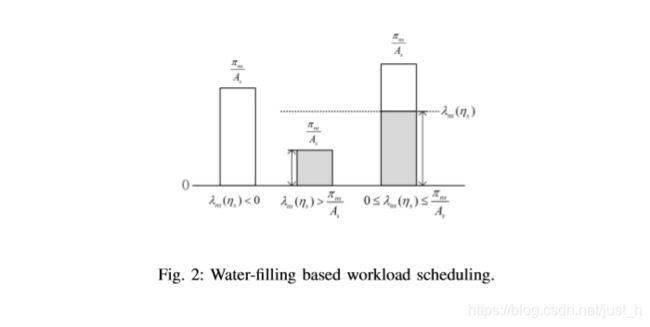
为了解决子问题耦合的挑战，我们将问题1表示为一个混合整数非线性规划问题，以联合优化服务缓存和工作负载调度。设计了一个两层迭代缓存更新(ICE)算法来说明这两个子问题的相互作用，外层迭代地更新基于Gibbs sampling的边缘缓存策略(服务缓存子问题)，内层优化工作负载调度策略(工作负载调度子问题)。为了正确权衡计算和通信延迟，我们使用排队模型来分析系统各部分的延迟，从而计算平均服务响应时间。当平均服务响应时间最小化时，可以实现适当的计算通信折衷。针对边异构引起的工作量调度指数复杂度问题，利用工作量调度子问题的凸性，提出了一种基于water filling思想的多项式计算复杂度的启发式工作量调度算法。

本文的贡献总结如下:

• 我们研究了移动边缘计算中的协同服务缓存和工作负载调度，旨在最小化服务响应时间和外包流量。我们将此问题表示为一个混合整数非线性规划问题，并通过分析该问题的简化案例来证明其非多项式复杂度。
• 利用排队模型分析了系统各部分的时延，在此基础上证明了工作量调度子问题的凸性。
• 我们提出了两层ICE来解决问题1，外层基于Gibbs sampling迭代地更新服务缓存策略，内层优化工作负载调度策略。利用工作量调度子问题的凸性，提出了一种基于water filling思想的计算复杂度较低的启发式工作量调度算法。
• 我们进行了大量的仿真来评估该算法的有效性和收敛性。
  本文组织如下。第二部分是对相关工作的回顾。第三部分对系统模型进行了分析，并给出了问题的解决方案。第四部分详细介绍了算法设计，第五部分给出了仿真结果。最后，第六部分为结束语。

III. SYSTEM MODEL AND PROBLEM FORMULATION

A. System Model
本文研究了移动边缘计算中的协同服务缓存和工作负载调度问题。如图1所示，附近的边缘节点通过局域网或有线点对点连接。对于没有缓存服务或没有提供足够计算能力的边缘节点，可以将相应的计算任务转移到附近未充分利用的边缘节点，这些边缘节点缓存了服务或将其外包给云。我们考虑一个由N ={1,2，…，N}边节点，每个边节点的计算能力Rn (n∈N)和存储能力Pn (n∈N)。系统提供了一个S ={1,2，…S}服务，如手机游戏、对象识别、视频流等，根据计算和存储需求进行区分。要在网络边缘处理一类移动应用，边缘节点需要提供一定的存储容量来缓存应用的服务。为每个服务,我们考虑到相应的计算任务的计算请求(在CPU周期)遵守βs的期望指数分布时,和任务到达每个边缘节点n是一个泊松过程预期的速率答,这是一个一般假设[7]。由于存在一个具有充足存储和计算能力的集中式云，因此云存储了所有的服务，而云dcloud中的处理延迟主要是由边缘节点到云的传输延迟造成的。
1)边缘缓存和工作负载调度策略: 在这项研究中应该回答两个问题:1)哪种边缘节点缓存每种类型的服务?2)缓存相同服务的连接边缘节点之间如何调度计算工作量?我们使用两组变量来建模边缘缓存和工作负载调度结果:cns 表示服务s是否缓存在边缘节点n上，λns代表在边缘节点n上执行的服务s的工作负载比。我们通过边缘缓存和工作负载调度策略来参考各自的向量:

2)服务响应时间:
用Θn表示与边缘节点n直接连接的附近边缘节点集，dn表示LAN到边缘节点n的传输延迟。在边缘节点n处执行的计算工作量不大于附近边缘节点的总到达任务，

在每个边缘节点上，计算容量由缓存的服务共享。设函数Γn表示边缘节点n的计算分配机制，即分配给服务s的计算容量为rns＝Γn（C）。对于每个服务s，响应计算任务的计算请求服从指数分布，边缘节点n的服务时间也服从指数分布，期望值为βs/rns。此外，服务到达边缘节点n的任务到达是期望为λnsAs的Poisson过程。因此，对于每个服务s，边缘节点n上计算任务的服务过程可以被建模为M/M/1队列，并且计算延迟为

当将任务外包到云端时，处理时间主要是由核心网络的传输延迟造成的。与边缘节点的任务到达相似，核心网络中的任务到达也是一个Poisson过程，其期望速率为λosAs。设ts为服务s的一个计算请求单元外包时的传输请求量（例如输入数据）（在CPU周期中）。这里，ts是一个与具体业务s[8][15]相关的常数。设ts为服务s(以CPU周期为单位)外包一个计算请求时的传输请求量(如输入数据)。这里，ts是与特定服务s[8]，[15]相关的常数。然后，对于服务s，相应任务的传输请求服从指数分布，期望为tsβs。任务在核心网络中的传输时间也服从期望的指数分布 tsβs/Bs ,其中，Bs为传输服务s的核心网络带宽，因此，核心网络的传输时延为
服务s的平均响应时间可以计算为系统各部分时延的加权和，包括边缘节点的计算时延、局域网上的传输时延和云上的传输时延，即

B. Problem Formulation
本文联合优化了edge服务缓存和工作负载调度策略，旨在最小化服务响应时间和整体云外包流量:

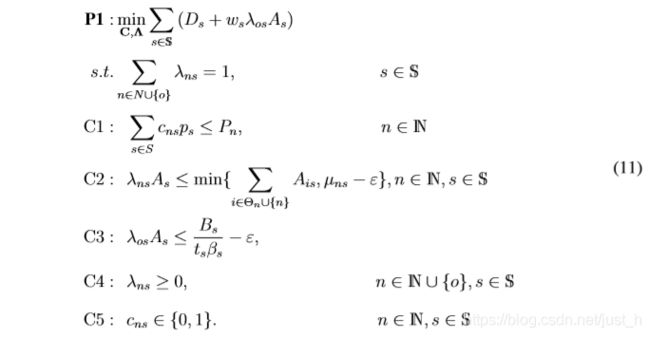
这里ws是一个权值常数，它与服务s外包任务时传输的数据流量呈正相关。约束C1确保每个边缘节点上的缓存服务不超过存储容量。C2是Eq.(4)和Eq.(6)的组合结果，保证每个边缘节点只接受附近边缘节点的计算请求，每个边缘节点调度的计算工作量不超过每个服务的计算能力。

C. Complexity Analysis
P1问题是一个混合整数非线性规划问题。在本节中，我们通过分析包括边缘节点之间不合作的简化情况并考虑一种单一类型的服务，提出了P1的非多项式计算复杂性。
1）Simplified Case 1: 边缘节点之间不合作:在第一种情况下，我们假设边缘节点之间不合作。根据这个假设，不同服务的计算任务要么在本地处理，要么直接外包给云。因此，外包给云的计算任务不仅取决于边缘计算能力，而且高度依赖于每个边缘节点的存储能力。在这个场景中，问题P1简化为服务缓存和任务资源外包问题，类似于[7]。具体来说，P1中边缘节点间的工作负载调度被简化为N个独立的任务外包子问题。每个边缘节点只需要决定外包计算请求λons(作为λons = 1λns)根据自己的服务缓存策略和计算能力的限制。[7]指出，由于服务缓存和任务外包问题仍然是一个混合整数非线性规划问题，并且具有非多项式的计算复杂度，因此减少服务缓存和任务外包仍然是一个具有挑战性的问题。
2)Simplified Case 2:考虑单一类型的服务: 在这个简化的例子中，我们假设系统中只考虑一种类型的服务。然后，每个边缘节点的缓存结果可以简单地由服务存储需求和边缘存储容量之间的关系来决定:如果服务有足够的存储容量，则缓存在一个边缘节点上;否则，服务不会缓存在边缘节点上。有了这个假设(即，给出了服务缓存策略C)，将问题P1简化为工作负载调度问题，将计算负载调度到具有足够缓存服务的存储容量的边缘节点上。
解决工作量调度问题具有两个方面的挑战性。首先，边缘节点在计算任务到达和边缘计算能力上是异构的。平衡异构边缘节点之间的工作负载对于最小化服务响应时间和外包到云的流量至关重要，但是，如果以集中式的方式实现，则会导致指数计算复杂性。其次，在边缘节点之间调度工作负载应该考虑计算传输的权衡。将计算任务从超载的边缘节点转移到附近的轻载边缘节点或转移到云上，有利于减少计算延迟，但同时也增加了传输延迟。最小化服务响应时间需求，以适当地平衡计算和传输延迟。通过总结上述两个简化的P1问题案例，可以看出，减少的服务缓存和任务外包以及工作负载调度问题都具有非多项式的计算复杂度。因此，P1问题也具有非多项式计算复杂度，降低计算复杂度是解决该问题的关键。

IV. ALGORITHM DESIGN

正如上一节所阐明的，即使是P1问题的简化情况也仍然具有非多项式计算复杂度。本节给出了算法设计的主要思想，该算法在降低计算复杂度的同时，联合优化了服务缓存和工作负载调度策略。具体来说，我们设计了一个两层迭代缓存更新算法(ICE)，外层更新基于Gibbs sampling[22]的服务缓存策略。在内层，给出了边缘缓存策略，并将问题P1简化为缓存了某一类型服务的边缘节点之间的工作负载调度子问题(类似于简化的情况2)。利用凸性分析证明了简化问题的指数计算复杂度，并进一步提出了一种基于注水思想的简化计算复杂度的启发式工作量调度算法(算法2)。

A. Iterative Caching updatE Algorithm (ICE)
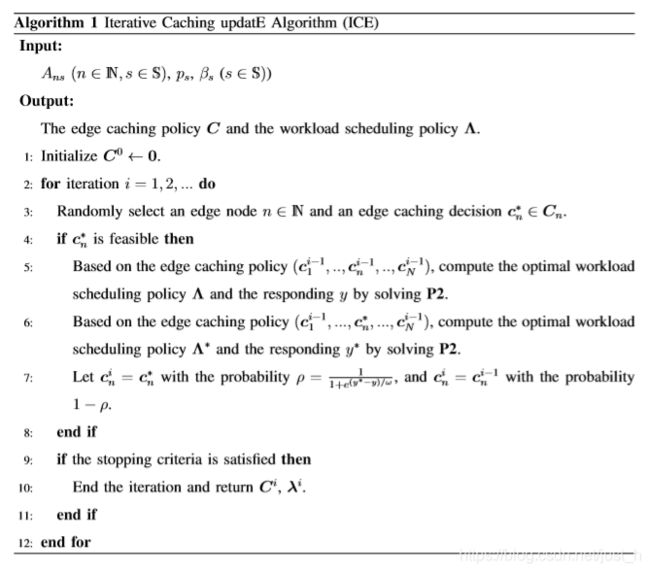
Gibbs sampling是一种蒙特卡罗马尔可夫链技术，它可以从条件分布样本中推导出多个变量的联合分布。Gibbs sampling的主要思想是通过遍历每个变量来模拟条件样本，同时在每次迭代中保持其余变量不变。蒙特卡罗马尔可夫链理论保证了由Gibbs sampling得到的平稳分布是目标联合分布[23]。在本文中，我们利用Gibbs sampling的思想迭代地确定最优的服务缓存策略，如算法1所示。算法的关键是将边缘缓存策略的条件概率分布与P1的目标联系起来(步骤7)，通过在每次迭代中对条件概率进行适当的设计，得到的平稳联合分布可以收敛到最优的高概率边缘缓存策略。ICE算法的工作原理如下。在每个迭代中，随机选择一个边缘节点n (n ∈ N)和一个可行的边缘缓存决策c ^* n，同时保持其余边缘节点的缓存决策不变(步骤3)。给定所有边缘节点的缓存策略，P1简化为工作负载调度子问题:

B.启发式工作量调度算法
当给出边缘缓存策略时，需要解决P2问题，计算最优的工作负载调度策略和相应的对象值。在这一部分，我们首先通过理论分析证明了P2的指数复杂度，并进一步利用问题的凸性提出了一种启发式的工作量调度算法。


一个凸优化问题可以通过搜索满足KarushKuhn-Tucker (KKT)条件[24]的结果来解决。我们首先提供P2的KKT条件。当缓存策略,计算资源分配给每个服务决心根据Γn ©。因此，对于一个服务，它与其他服务之间的工作负载调度策略是相互独立的。解决问题等同于为每种类型的服务优化工作负载调度策略。任务a服务s (s∈s)为代表。定义拉格朗日函数为


2)算法设计:该算法的主要思想是首先去掉边缘节点的计算能力约束和核心网络的传输带宽约束(即， P2)中的不等式约束，推导出边缘节点的工作负载调度结果与云的相关性。然后在资源约束条件下寻找满足KKT条件的最优解。当去除不等式约束时，KKT条件只保留(C1)和(C3)在(15)中，(C1)变为

V. SIMULATION RESULTS

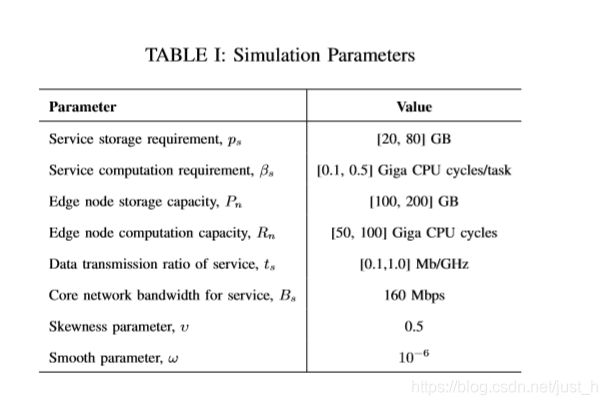
在本节中，我们将进行大量的仿真来评估我们的算法。我们模拟了一个覆盖12个边缘节点的100m×100m区域，共提供8个服务。边缘节点具有异构存储和计算能力，均服从均匀分布。计算任务在不同边节点An (n∈N)上的总到达率是均匀分布的。在每个边缘节点上，服务的流行程度遵循Zipf的分布，即,χns∝rs^−υ年代,rs是服务的秩s，v是偏度参数[10]。因此，服务s在边缘节点n上的计算任务到达率可以计算为Ans＝χns·An，其中An是边缘节点n上计算任务的总到达率，主要参数见表一。
比较了两种基准算法的性能。
非合作算法[8]：边缘节点根据Gibbs采样缓存服务。在每个边缘节点，服务的计算工作负载要么在本地处理，要么外包给云。
贪婪算法：边缘节点根据人气缓存服务。流行的服务在边缘节点上具有更高的缓存优先级。对于缓存服务，每个边缘节点优化本地处理和外包给云的工作负载，以最小化边缘处理延迟和外包流量。


A. Performance Comparison
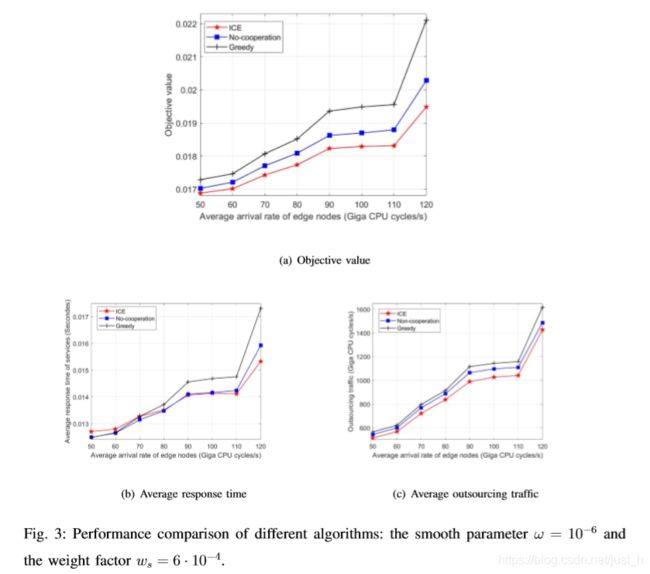
通过改变边缘节点上任务的平均到达率(即任务到达时间)，我们比较了三种算法的目标值、总服务响应时间和外包流量。结果如图3所示。
与非合作算法和贪婪算法相比，我们的合作算法总能产生最小的目标值和外包流量，并接近于最小的服务响应总时间。在贪心算法中，所有的边缘节点都以高优先级缓存热门服务，因此不热门服务的计算任务不得不外包给云。此外，贪婪算法只依赖于服务的流行度来确定边缘缓存策略，而不考虑服务的存储需求。在边缘节点上缓存具有低存储需求的多个不太流行的服务，与缓存具有大存储需求的一个流行服务相比，更有利于充分利用计算和存储能力。基于Gibbs sampling的合作和不合作算法缓存服务，同时考虑了服务的存储需求和服务的受欢迎程度。因此，与其他两种算法相比，贪心算法通常会导致更多的外包流量和服务响应时间。不合作算法由于边缘节点之间缺乏协作，使得存储容量较低的边缘节点的计算能力不能得到充分利用。在协同算法中，通过对连接的边缘节点之间的服务缓存和工作负载调度的仔细设计，可以协调并充分利用边缘节点的存储和计算能力。

B. Convergence of ICE
根据理论分析在定理1中,吉布斯抽样基础服务缓存算法(算法1)可以服务缓存结果以概率1收敛于最优平滑参数ω时接近0。这部分说明了ω对冰的收敛结果图4所示。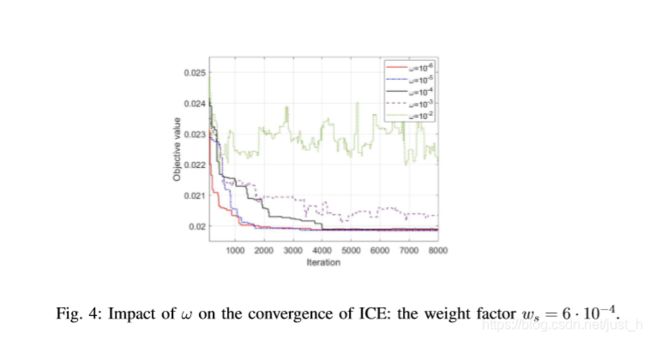
如图4所示,客观价值可以收敛算法的结果当ω≤10−4,和ω降低收敛速度更快。当ω≥10−3,更高价值的客观价值收敛缓慢(ω= 10−3)甚至不收敛(ω= 10−2)。这些结果可以用ICE的Step 7和Eq.(23)来解释。根据小冰,ω,越可能选择边缘节点更新更好的缓存决定在每个迭代中。因此,当ω很小,客观价值收敛迅速(在更少的迭代)。此外,它可以从情商的结论。(23),固定的概率最优缓存结果随ω,和概率→1ω→0。因此,较小的ω,冰可能收敛于最优缓存结果。

C. The Impact of Edge Node Connectivity
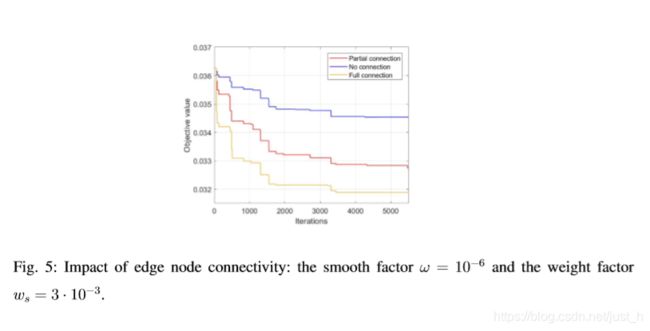
分析了边缘节点连通性对ICE性能的影响。如图5所示，所有边缘节点连接的系统收敛到最小目标值，而没有连接边缘节点的系统收敛到最大目标值。在所有边缘节点连接的系统中，通过在所有边缘节点之间调度工作负载，可以在系统级实现协作的好处。当边缘节点部分连接时，只能在集群内探索合作的好处(集群内的边缘节点是连接的，不同的集群之间没有连接)。因此，边缘节点之间的连接程度越高，ICE的合作效益就越大。

VI. CONCLUSIONS

本文研究了移动边缘计算中的协同服务缓存和工作负载调度问题。基于排队分析，将该问题转化为一个混合整数非线性规划问题，并证明该问题具有非多项式计算复杂度。为了解决子问题耦合、计算通信权衡和边缘节点异构等问题，我们提出了基于Gibbs sampling的ICE，以迭代的方式实现接近最优的服务缓存策略。提出了一种基于注水的工作量调度算法，该算法的计算复杂度为多项式。通过大量的仿真验证了该算法的有效性和收敛性，并进一步分析了边缘连通性的影响。