音频噪声抑制(2):维纳(Wiener)滤波器篇
之前的文章讲了使用经典滤波器来抑制噪声。
Review:噪声抑制之经典滤波器篇
里面提到,“用经典滤波器抑制噪声,非常简单。如果噪声的功率谱PSD和有用信号功率谱PSD没有重叠的话,那可以实现非常好的效果。
但是,如果有重叠,去噪的效果就不是特别理想了。因为在复指数信号空间里面,没办法把有用信号和噪声信号分离啊。”
正是由于“噪声谱和有用信号谱可能重叠”,所以发展了维纳滤波器。
前面的文章对维纳滤波器的设计也讲过了。
Review:维纳滤波器的设计
这篇文章,就是真实地来操作一下,设计一个维纳滤波器来抑制噪声。
因为没有去录音,所以噪声源还是matlab里的randn产生的高斯过程的数据。
再假设高斯过程并不是直接加入有用数据的,而是经过了一个“信道”,发生了一些变化,比如,AR过程。
然后就是分两步了。
1. 训练过程,用已知的训练信号和已知的接收信号,通过解方程,求得滤波器系数;
2. 滤波器系数不变,用这组系数对此后接收到的信号进行滤波,实现噪声抑制。
代码比较简单,所以直接出来了。
主函数。
%% 维纳去噪,基于训练的
% 通过解方程求滤波器系数
% 作者:qcy
% 版本说明:补充滤波阶段
% 版本:v1.1
% 时间:2016年10月29日18:18:21
% 版本说明:训练阶段
% 版本:v1.0
% 时间:2016年10月29日16:52:37
clear;
close all;
clc
%% 读入音频
filedir=[]; % 设置路径
filename='bluesky1.wav'; % 设置文件名
fle=[filedir filename]; % 构成完整的路径和文件名
[s, fs] = audioread(fle); % 读入数据文件
s=s-mean(s); % 消除直流分量
s=s/max(abs(s)); % 幅值归一
N=length(s); % 语音长度
time=(0:N-1)/fs; % 设置时间刻度
%% 产生噪声并加入
SNR = 0; % 设置信噪比
r2=randn(size(s)); % 产生随机噪声
b=fir1(31,0.5); % 设计FIR滤波器,代替H
r21=filter(b,1,r2); % FIR滤波
% [signal_with_noise,noise]=add_noisedata(s,data,fs,fs1,snr);
[r1,r22]=add_noisedata(s,r21,fs,fs,SNR);% 产生带噪语音,信噪比为SNR
%% 解方程
% 【训练阶段】
h_length = 100; % 这个东西我目前所知道的,就只有凭感觉去设置了。
desired_signal = s;
observed_signal = r1;
h = my_weiner_filter1( h_length,desired_signal,observed_signal );
% 滤波
% 用维纳滤波器,作用在接收到的训练信号上。看看效果-->这还是属于训练阶段
y = filter(h,1,r1);
output = y;
snr1=SNR_singlech(s,r1); % 计算初始信噪比
snr2=SNR_singlech(s,output); % 计算滤波后的信噪比
snr=snr2-snr1;
%% 画图
figure;
subplot 311; plot(time,s,'k'); ylabel('幅值');
ylim([-1 1 ]); title('原始语音信号');
subplot 312; plot(time,r1,'k'); ylabel('幅值')
ylim([-1 1 ]); title('带噪语音信号');
subplot 313; plot(time,output,'k');
ylim([-1 1 ]); title('滤波输出语音信号');
xlabel('时间/s'); ylabel('幅值')
%% 打印SNR
fprintf('[训练]\n',snr1);
fprintf('滤波前 SNR = %f [dB] \n',snr1);
fprintf('滤波后 SNR = %f [dB] \n',snr2);
fprintf('提升 %f [dB] \n',snr);
fprintf('\n');
%% 听效果
% sound(s,fs); % 干净的语音
% sound(r1,fs); % 含噪的语音
% sound(output,fs); % 滤波后的语音
%% 【降噪阶段】
% 假设这是后来录的一段音,混入了性质类似的噪声。
% 现在想用刚刚得到的滤波器系数,来去除掉现在这段含噪信号中的噪声。
filedir=[]; % 设置路径
filename='risesun.wav'; % 设置文件名
fle=[filedir filename]; % 构成完整的路径和文件名
[s, fs] = audioread(fle); % 读入数据文件
s=s-mean(s); % 消除直流分量
s=s/max(abs(s)); % 幅值归一
N=length(s); % 语音长度
time=(0:N-1)/fs; % 设置时间刻度
%% 产生噪声并加入
% SNR = 0; % 设置信噪比
r2=randn(size(s)); % 产生随机噪声
b=fir1(31,0.5); % 设计FIR滤波器,代替H
r21=filter(b,1,r2); % FIR滤波
% [signal_with_noise,noise]=add_noisedata(s,data,fs,fs1,snr);
[r1,r22]=add_noisedata(s,r21,fs,fs,SNR);% 产生带噪语音,信噪比为SNR
%% 用上一阶段求得的h,降噪
% 滤波
y = filter(h,1,r1);
output = y;
snr1=SNR_singlech(s,r1); % 计算初始信噪比
snr2=SNR_singlech(s,output); % 计算滤波后的信噪比
snr=snr2-snr1;
%% 画图
figure;
subplot 311; plot(time,s,'k'); ylabel('幅值');
ylim([-1 1 ]); title('原始语音信号');
subplot 312; plot(time,r1,'k'); ylabel('幅值')
ylim([-1 1 ]); title('带噪语音信号');
subplot 313; plot(time,output,'k');
ylim([-1 1 ]); title('滤波输出语音信号');
xlabel('时间/s'); ylabel('幅值')
%% 打印SNR
fprintf('去噪 \n',snr);
fprintf('滤波前 SNR = %f [dB] \n',snr1);
fprintf('滤波后 SNR = %f [dB] \n',snr2);
fprintf('提升 %f [dB] \n',snr);
%% 听效果
% sound(s,fs); % 干净的语音
% sound(r1,fs); % 含噪的语音
sound(output,fs); % 滤波后的语音维纳滤波器设计的函数。
function h = my_weiner_filter1( h_length,desired_signal,observed_signal )
%function h = my_weiner_filter1( h_length,desired_signal,observed_signal )
% 维纳滤波器的实现
% 输入参数
% h_length: 返回的FIR滤波器的长度
% desired_signal: 所期望的信号,训练信号,干净信号
% observed_signal: 观测到的信号
% 返回参数
% h: FIR滤波器系数
%
% 作者:qcy
% 版本:v1.0
% 时间:2016年10月29日18:50:56
% 0. 定义线性方程组的大小
row_number = h_length;
col_number = row_number;
% 1. Rx --> observed_signal
M = col_number;
% lags = -(N-1):(N-1);
Rx_c_full = xcorr(observed_signal);
[~,k] = max(Rx_c_full);
Rx_c = Rx_c_full(k:k+M-1);
Rx_c = Rx_c.';
% 2. Rdx
Rdx_c_full = xcorr(desired_signal,observed_signal);
Rdx_c = Rdx_c_full(k:k+M-1);
% 3. 求h, Ax = b
% (1) 生成自相关A阵
A = toeplitz(Rx_c,Rx_c);
b = Rdx_c;
h = A\b;
end其中,加入噪声的代码如下。
function [signal,noise]=add_noisedata(s,data,fs,fs1,snr)
s=s(:); % 把信号转换成列数据
s=s-mean(s); % 消除直流分量
sL=length(s); % 求出信号的长度
if fs~=fs1 % 若纯语音信号的采样频率与噪声的采样频率不相等
x=resample(data,fs,fs1); % 对噪声重采样,使噪声采样频率与纯语音信号的采样频率相同
else
x=data;
end
x=x(:); % 把噪声数据转换成列数据
x=x-mean(x); % 消除直流分量
xL=length(x); % 求噪声数据长度
if xL>=sL % 如果噪声数据长度与信号数据长度不等,把噪声数据截断或补足
x=x(1:sL);
else
disp('Warning: 噪声数据短于信号数据,以补0来补足!')
x=[x; zeros(sL-xL,1)];
end
Sr=snr;
Es=sum(x.*x); % 求出信号的能量
Ev=sum(s.*s); % 求出噪声的能量
a=sqrt(Ev/Es/(10^(Sr/10))); % 计算出噪声的比例因子
noise=a*x; % 调整噪声的幅值
signal=s+noise; % 构成带噪语音
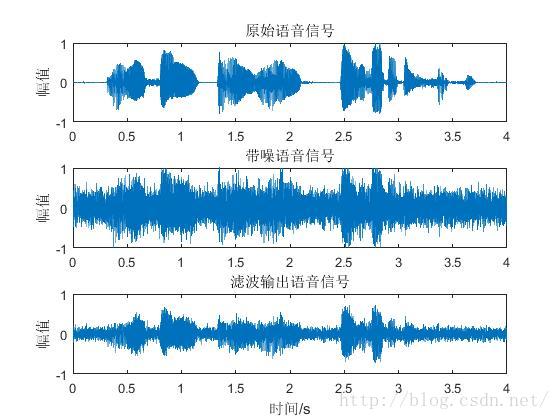
效果示意图。
训练阶段。
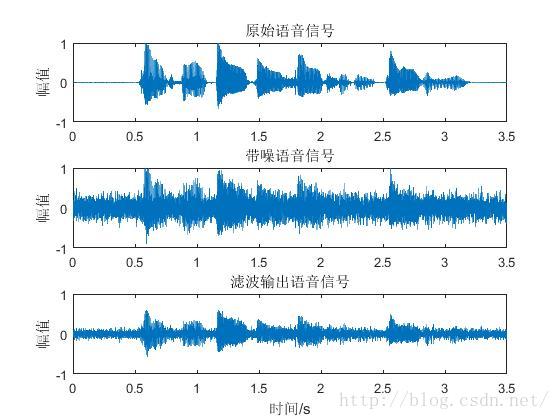
滤波阶段。
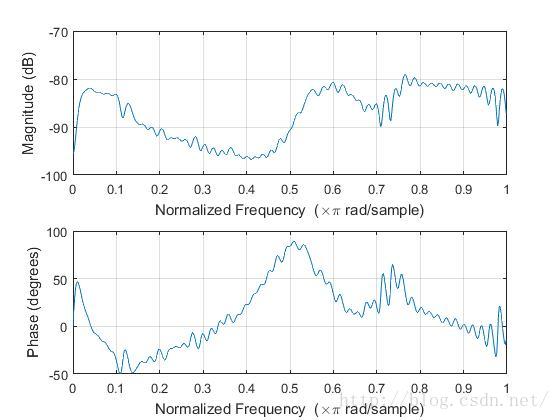
求解方程得到的滤波器的频率响应。
看得出来,因为是语音嘛,所以,设计出来的滤波器的性质可能更多的还是低通…
总之,这是一种在整个频率范围内的,均方意义下的最优……
最后,因为维纳滤波器的前提是,信号与噪声不相关,信号与噪声宽平稳,……
反正约束条件还是挺多的,所以,虽然对信号的噪声抑制效果,比经典滤波器的要好,
但是,为了得到更好的效果,还需要利用更先进的技术。比如,之后要讲的,自适应滤波器(adaptive filter)。
谢谢观赏。
敬请期待。