Leetcode——BFS,DFS穿插一下 / 第五天prepare 1/2(102,207,bfs差三题,78,46,90,47,22,79未,后
发现在做二叉树的时候,就是递归、深度遍历、广度遍历这样的组合,想着还是将BFS, DFS理清楚吧,对做题参考答案都有更好理解吧,什么时候用BFS什么时候用DFS反应更快一点……
//深度优先搜索和广度优先搜索广泛运用于树和图中
BFS

广度优先搜索一层一层地进行遍历,每层遍历都是以上一层遍历地结果作为起点,遍历所有一个距离能访问到的节点。需要注意的是,遍历过的节点不能被再次遍历

每一层遍历的节点都与根节点距离相同。设Di表示第i个节点与根节点的距离,自然,先遍历的节点i与后遍历的节点j,有Di
在实现BFS时需要考虑一下问题:
- 队列:用来存储每一轮遍历得到的节点
- 标记:对于遍历过的节点,应该将它标记,防止重复遍历
BFS模板看看:
二叉树层序遍历和拓扑
二叉树层序遍历(102)
解题思路:
BFS,广搜(层序遍历),建立一个queue,每一层的数据放入队列中,同时维护一个vector,将每一层的数据放入到一维的vector中,一层结束就将一维的放入到二维的结果vector中
代码:
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {//返回结果是一个二维的数组向量
vector<vector<int>> res;
if(!root) return res;
queue<TreeNode*> q{{root}};//维护一个队列,初始将根节点放入队列中
while(!q.empty())
{
int size = q.size();
vector<int> layer;//要初始化 vector layer(size,0);
for(int i = 0; i<size; i++)
{
TreeNode * t = q.front();q.pop();
layer.push_back(t->val);
if(t->left) q.push(t->left);
if(t->right) q.push(t->right);
}
res.push_back(layer);
}
return res;
}
};
问题:
1 取队列的第一个是q.first(), 是q.front(),不是q.top(),诶呀。
2 最后要记得返回结果
3 while循环条件,判断队列是否为空要!q.empty(),不是直接!q,跟链表是不一样的,哦哟过过脑好不
课程清单(207)

各个课程之间有依赖关系,现给出一个课程数以及课程间的依赖关系问是否能将课上完
思路
关于拓扑排序:拓扑排序为其所有结点的一个线性排序(对于同一个有向图而言可能存在多个这样的结点排序)。该排序满足这样的条件——对于图中的任意两个结点u和v,若存在一条有向边从u指向v,则在拓扑排序中u一定出现在v前面。-----> 课程0得先上才能上课程1即0---->1
1,先根据给出的课程间依赖关系建表,并初始化每个节点的入度
2,入度为0的入队列,对列表进行遍历,弹出的节点下的节点其入度都减1
3,最后弹出的所有的元素是否和课程元素相等,即能不能上完所有的课
代码
class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
//先根据输入来建立有向图,并将入度数组也初始化好
unordered_map<int, vector<int>> map;//这个图是什么意思,(int, 数组)
vector <int> degree(numCourses,0);//初始化每个节点的入度为0 vector是一个数组
for(vector<int> prerequisites : prerequisites) //
{
map[prerequisites[1]].push_back(prerequisites[0]);//写法,冒号前的是操作的,冒号后的是前面的
degree[prerequisites[0]]++;
}//表创建完毕
//开始栈操作
int count = 0;
queue<int> q;
for(int i = 0; i<numCourses; ++i)
{
if(degree[i] == 0) q.push(i);
}//第一批入队列,开始遍历队列
while(!q.empty())
{
int cur = q.front();
q.pop();
count++;
for(int next : map[cur])//找cur下的那些next
{
degree[next] -- ;
if(degree[next] == 0)
{
q.push(next);
}
}
}
return count == numCourses;
}
};
问题
几个我不会的新写法:
在建立图的时候:
1,定义一个图,有向图就是各个节点之间的关系,一个节点指向一组节点,unordered_map
2,入度为一个数组:vector
3,根据给的依赖关系建表:
for(int i = 0;
for(vector
map[prerequisite[1]].push_back(prerequisite[0]);
degree[prerequisite[0]]++;}
4,队首元素出队列时,要去图中将队首元素指向的元素的入度都减1,我们要去找到cur下的元素都有哪些的时候for(int next : map[cur]),next就是找到的元素们
★★ 在hint中表示这道题还可以用DFS做的,mark一下,待会再见
做两道题清醒一下:
1. 计算在网络中从原点到特定点的最短路径长度(1091)
2. 组成整数的最小平方数数量(279)
For example, given n = 12, return 3 because 12 = 4 + 4 + 4; given n = 13, return 2 because 13 = 4 + 9.
可以将每个整数堪称图中的一个节点,如果两个整数之差为一个平方数,那么这两个整数所在的节点就有一条边,要求解最小的平方数数量,就是求解从节点n到节点0的最短路径(本题也可以用DP做)★★★
3. 最短单词路径(127)
题目:
DFS
可以划分为两大类问题:permitation和combination,即排列和组合
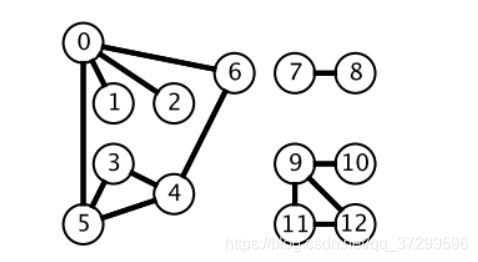
广度优先搜索是一层一层遍历,每一层得到的所有新节点要用队列存储起来以备下一层遍历的时候再遍历,而深度优先搜索在得到一个新节点时立即对新结点进行遍历:
从节点0出发开始遍历,得到新节点6时,立马对新节点6进行遍历,得到新节点4;
如此反复以这种方式遍历新节点,直到没有新节点了,就返回,然后继续以上步骤,
如,0 5 3返回到5, 4 6 返回到4 返回到5 返回到0 2 返回到0 1,遍历结束0534621
从一个节点出发,使用DFS对一个图进行遍历时,能够遍历到的节点都是从初始节点可达的,DFS常用来求解这种可达性问题。
在程序实现DFS时需要考虑以下问题:
- 1 栈:用栈来保存当前节点信息,当遍历新节点返回时能够继续遍历当前节点。可以使用递归栈
- 2 标记:和BFS一样需要对已经遍历过的节点进行标记
DFS也先看看简单题找找模板
(是一对题加其follow up)
子集(78)
思路
1,先写主体函数:定义一个结果,一个dfs语句里面参数传递(题给,位置,结果),一个返回结果
2,写dfs函数,首先判断退出条件,然后开始做选择
3,本题中就是对每个位置的值有两种选择情况,选或者不选
代码
class Solution {
public:
void dfs(vector<int>& nums, int pos, vector<int> &layer, vector<vector<int>> &res){
//注意返回值,直接void吧,因为结果res会自己更新的
//先考虑退出条件
if(pos == nums.size())
{
res.push_back(layer);//因为表示是一个ok的链表结束了,当然要压栈
return;
}
//开始, 第一种情况,pos等于0的情况,最最开始函数调用就是直接走到这里的
layer.push_back(nums[pos]);//选要,压栈
dfs(nums, pos+1,layer, res);
layer.pop_back();//选不要,把刚刚压入栈的元素给弹出去还,pop_back()里面是没有参数的
dfs(nums, pos+1,layer, res);
}
vector<vector<int>> subsets(vector<int>& nums) {
vector<vector<int>> res;
vector<int> layer;
dfs(nums, 0, layer, res);
return res;
}
};
问题
1,关于dfs函数中的参数:result就直接在dfs里递归更新,所有就要把result放进去迭代更新,对每一个解也要进行一个更新,因为list不是一下子就选出来的,而是对每一个数字进行判断,如果符合要求就加入到结果集中这样。当然题给的待分成子集的数组也是要传进去的。另外,一般DFS都会要记录一个当前的位置,比如现在是在判断第2个元素……,那一开始肯定就是0位置,选或不选
一般用dfs解决的简单点的题目的主题函数就是这么几行,定义一个结果,一个dfs,返回一个结果,复杂点的话会涉及到去重的问题
2,在dfs中首先考虑其退出条件,然后别忘记return语句啊
全排列(46)
思路:
是排列问题,首先每一位都得选数字,而且每个数字只能被选一次,已经选过的就不能再选了,会涉及到去重的问题,分如果选了这个数再dfs和不选这个数再dfs两种情况,可是对这个数就只是操作一次的,所以先进行选这个数的话标记点就会改变,再变成第二种情况标记点就需要重置:
1, 还是函数主体先写,定义一个结果,返回一个结果,一个dfs,参数还是题给,位置,结果
2, 写dfs内部,首先写退出条件,还是pos到最后一个就退出
3,开始:考虑去重的话就需要设置visited数组,回到主函数中初始化visited,并作为dfs的参数加进去,然后 —— 一共多少个数我们需要去一一做判断,设i,依次去做决定选还是不选,pos还是我们在“构建”的layer中的位置,到数了就可以加入结果集中。
4,如果这个数没有被取走,我就有权要或者不要,要了就加入layer中并设置标记,以这样的状态pos+1再次进入dfs来获取下一个位置的信息;如果不要,改回刚刚的标志位信息,不进入dfs循环的,因为当前pos位还没有确定,还要去i那边看有没有还没有没取走的值
代码:
//这题就要考虑一个去重的状态,如果已经访问过了那么久置visited = 1,如果回退的话就又重置0
//相当于123是放在那边的,然后你去选3个数,如果选过1了就不能再选了,只能在没选过的地方去选,对每一个数设置一个visited数组
class Solution {
public:
void dfs(vector<int>& nums, int pos, vector<int>& layer, vector<vector<int>>& res,vector<int>& visited)
{
//先考虑退出条件
if(pos == nums.size())
{
res.push_back(layer);
return;
}
for(int i = 0; i<nums.size(); i++)//i和pos分别是?
{
if(!visited[i])
{
layer.push_back(nums[i]);
visited[i]=1;
dfs(nums, pos+1, layer, res, visited);
//layer.pop_back();
visited[i] = 0;
layer.pop_back();
//dfs(nums, pos+1, layer, res, visited);//如果不要,那还有选择的机会的呀
}
}
}
vector<vector<int>> permute(vector<int>& nums) { vector<vector<int>> res;
vector<int> layer;
vector<int> visited(nums.size(),0);//初始化为0
dfs(nums, 0,layer, res,visited);
return res;
}
};
问题:
注意:
1,i和pos分别作用在 题给的数组nums上 和我们在“构建”的layer上, 所以确定要了的话,压入layer的是nums[i],进入dfs的是pos+1;
2,如果选择不要这个数,那么重置visited后,是不进入dfs循环的,而是继续去看题给nums的下一个数,直到选择一个数确定当下pos的值。
√
子集Ⅱ(90)
思路:
组合问题,跟上一题比不允许有重复的存在**,设定规则** :如果和前一个数相同,则只有选了第一个时才能自由选择第一个或者第二个,否则第一个不选第二个就不选
因为是一题follow up,所以我们先写第一种低配版情况,然后再去更改
1,写完78subset的代码,然后考虑规则,需要visited来标记是否可以去自由选择:
如果没有前一个元素即是首元素的话就可以有“选择”的权利,如果和前一个数不相同也ok,或者前一个数被选择了
2, 如果不满足条件的话就只能不添加元素的(保持layer),pos+1,继续dfs
代码:
class Solution {
public:
void dfs(vector<int>& nums, int pos, vector<int>& layer, vector<vector<int>>& res,vector<int>& visited)
{
//退出条件
if(pos == nums.size())
{
res.push_back(layer);
return;
}
if(pos == 0 || nums[pos]!= nums[pos-1] || visited[pos-1])
{
layer.push_back(nums[pos]);//要, 现在要是有条件的,不能想要就要了
visited[pos] = 1;
dfs(nums, pos+1, layer, res,visited);
layer.pop_back();//不要
visited[pos] = 0;//不要忘记置0
}
dfs(nums, pos+1, layer, res,visited); //如果没有满足上述if内的情况,就只能不要了
}
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
//要保证是有序的,才可以让相同的数在一起
sort(nums.begin(), nums.end());
vector<vector<int>> res;
vector<int> layer;
vector<int> visited(nums.size(),0);
dfs(nums, 0, layer, res,visited);
return res;
}
};
问题:
1,要保证相同的数是在一起的,需要对题给的数组进行sort排序
2,在确定选择或者不选择的时候都要记得visited的状态
3,第一次submit时没有排序以及没有更改visited == gg
√
全排列Ⅱ(47)
思路
是上两题排列的follow up,因为题给中有相同的值所以直接全排列会有重复的layer产生,还是要指定规则,由由于是排列,所以i也是要有的,总之大概有思路之后就先写写看,模板么写上去:
1, 排列,所有有i,因为要去重那么visited也要到位,是由于相同元素造成的,所以要制定规则
代码
//由于相同的数导致产生重复元素,规则:相同的数,只有前一个数被选择,第二个数才可以自由选择或不选择,否则就只能不被选择
class Solution {
public:
void dfs(vector<int>& nums, int pos, vector<int>& layer, vector<vector<int>>& res,vector<int> &visited)
{
if(pos == nums.size()) //退出条件
{
res.push_back(layer);
return;
}
for(int i = 0; i<nums.size(); ++i)
{
//首先只有没有被访问的元素才可以进入被筛选队列
if(!visited[i] && (i == 0||nums[i] != nums[i-1] || visited[i-1]))
{//有选择权了
layer.push_back(nums[i]);
visited[i] = 1;
dfs(nums, pos+1, layer, res,visited);
layer.pop_back();
visited[i] = 0;//如果不选择的话不可以进入下一个dfs哦
}
}
}
vector<vector<int>> permuteUnique(vector<int>& nums) {
sort(nums.begin(), nums.end());//这次先排序有记得了
vector<int> visited(nums.size(), 0);
vector<vector<int>> res;
vector<int> layer;
dfs(nums, 0, layer, res,visited);
return res;
}
};
问题
在一个位置确定之后,pos要加1,在代码中就要写pos+1,写pos++,++pos都报错了
开始稍微复杂DFS:
dfs的模板还是那个模板,就是参数根据题意会变化一下,主体内容也要灵活变动一下,代码就是边想边加东西,但是思路还是多看视频和别人的讨论比较好,实现要自己摸索出来,这样思路和动手相辅相成才正道
1. 生成括号(22)
思路
生成满足条件的括号序列,dfs,返回的结果是一个一维数组,因为里面的元素是string,虽然有很多字符,但是构成一个字符串,所以是一个字符串数组
1, 括号需要左右对比,题给的参数是n即n对括号,最后的字符串是2n个符号,n个左括号,n个右括号,所以传入参数中题给部分变为n,n表示左右括号
2,dfs内还是先考虑退出条件,就是左右括号都出去了,值都成为0了
3,左括号不可以比右括号少
代码
class Solution {
public:
void dfs(int left, int right, string layer, vector<string> & res)//layer不要引用
{
if(left == 0 && right == 0) //退出条件
{
res.push_back(layer);
return;
}
if(left>0)//这个表达的意思是满足这个条件就得加左括号,嗯……还是说这两个if是并行操作的,不一定到哪一个去?
{
dfs(left-1,right, layer + "(", res);
}
if(left<right)
dfs(left, right-1, layer + ")",res);
}
vector<string> generateParenthesis(int n) {
vector<string> res;
string layer = "";//不确定字符串是不是这么定义的,好像这行是没有用的
//dfs,按理是传入一个题给数3,就是3对括号,6个字符咯,其实就是左括号和右括号分别n个,所以这次题给就两个数
dfs(n,n,"", res);
return res;
}
};
问题
1,string不可以加引用,说string是一个临时变量,不可以给临时变量加引用,如果要加的话就需要
void dfs(int left, int right, const string& layer, vector<string> & res){……}
![]()
![]()
感谢https://www.cnblogs.com/area-h-p/p/11498481.html解答
再测试传入的参数中改变leftint &left, int right,报错,但是const int &left, int right, 加const就没问题
√
2. 词语搜索(79) (后三题都,塔罗兔20200214直播
思路
代码
问题
3. N皇后 hard(51)
4. 求解数独hard(37)
平静一下再做几题:
1. 查找最大的连通面积(695)
2. 矩阵中的联通分量(200)
3. 好友关系的联通分量数目(547)
好友关系可以看成一个无向图,例如第0个人与第1个人是好友,那么M[0][1]和M[1][0]的值都为1
4. 填充封闭区域(130)
5. 能到达的太平洋和大西洋的区域(417)

左边和上边是太平洋,右边和下边是大西洋,内部的数字代表海拔,海拔高的地方的水能够流到低的地方,求解水能够流到太平洋和大西洋的所有位置
(哇,这种题,好吓人)