图论第一发————最短路
图 n个点 ，m条边（点，边都可以有权值）
存储 邻接矩阵 n*n （基本被淘汰啦）
临接表
核心代码没几行 临接表
有向图 m
无向图 2*m
#include
#include
#include
#include
#include
using namespace std;
int num=0;
int head[10005]={0},nxt[10005]={0},to[10005]={0},v[10005]={0};
int n,m;
void add(int x,int y,int z);
{
num++;
nxt[num]=head[x]; //head（x点连的第一条边）
head[x]=num; //nxt （一条边后的另一条边）
to[num]=y;
v[num]=z;
}
int main()
{
scanf("%d%d",&n,&m);
int x,y,z;
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
//add(y,x,z); //无向图
}
return 0;
}
任意两点间的最短路
Floyd算法
- 本质 dp D[i,j]=min ( D[i,j] , D[i,k]+D[k,j] ) D[i,j] 最后出现最短路
- 阶段 k 最外层
- 时间复杂度 （
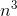） 空间复杂度（
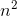） - 核心代码只有四行
for(int k=1; k<=n; k++)
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
a[i][j]=min(a[i][k]+a[k][j],a[i][j]);
这种算法可以找多源最短路，想知道a点到b点最短路，只能加入中间点来缩短路径，比如a到b 加入中间点k a到k到b
那么我们可以这样判断，要知道i到j的最短路，我们只要判断e[i][j]是否大于e[i][1]+e[1][j]即可，而中间值1则要用for循环从1到n遍历一个遍，就是查找所有中间值
#include
#include
#include
#include
#include
using namespace std;
int n,m;
int a[1005][1005]={0};
int main()
{
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
a[i][j]=2147483647;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
scanf("%d",&a[i][j]);
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
a[i][j]=min(a[i][k]+a[k][j],a[i][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
printf("%d ",a[i][j]);
return 0;
}
单源最短路
Dijkstra
只适用于非负边的图
更新一个点的dis=另一点的dis+一条边的边权
所以dis最小的点不会再被更新，所以最小的点的dis一定是正确的答案，用它再去更新其他的点
所以每次从优先队列出来时就找到这个点正确的dis
用b数组标记是否出队
由于优先队列不能对其中的点直接进行修改，所以会多次入队，共 n+m 次
例如求下图中的 1 号顶点到 2、3、4、5、6 号顶点的最短路径。
图中关系如下图：
我们还需要用一个一维数组 dis 来存储 1 号顶点到其余各个顶点的初始路程，如下。
我们将此时 dis 数组中的值称为最短路的“估计值”。
既然是求 1 号顶点到其余各个顶点的最短路程，那就先找一个离 1 号顶点最近的顶点。通过数组 dis 可知当前离 1 号顶点最近是 2 号顶点。当选择了 2 号顶点后，dis[2]的值就已经从“估计值”变为了“确定值”，即 1 号顶点到 2 号顶点的最短路程就是当前 dis[2]值。为什么呢？你想啊，目前离 1 号顶点最近的是 2 号顶点，并且这个图所有的边都是正数，那么肯定不可能通过第三个顶点中转，使得 1 号顶点到 2 号顶点的路程进一步缩短了。因为 1 号顶点到其它顶点的路程肯定没有 1 号到 2 号顶点短，对吧 O(∩_∩)O~
既然选了 2 号顶点，接下来再来看 2 号顶点有哪些出边呢。有 2->3 和 2->4 这两条边。先讨论通过 2->3 这条边能否让 1 号顶点到 3 号顶点的路程变短。也就是说现在来比较 dis[3]和 dis[2]+e[2][3]的大小。其中 dis[3]表示 1 号顶点到 3 号顶点的路程。dis[2]+e[2][3]中 dis[2]表示 1 号顶点到 2 号顶点的路程，e[2][3]表示 2->3 这条边。所以 dis[2]+e[2][3]就表示从 1 号顶点先到 2 号顶点，再通过 2->3 这条边，到达 3 号顶点的路程。
我们发现 dis[3]=12，dis[2]+e[2][3]=1+9=10，dis[3]>dis[2]+e[2][3]，因此 dis[3]要更新为 10。这个过程有个专业术语叫做“松弛”。即 1 号顶点到 3 号顶点的路程即 dis[3]，通过 2->3 这条边松弛成功。这便是 Dijkstra 算法的主要思想：通过“边”来松弛 1 号顶点到其余各个顶点的路程。
同理通过 2->4（e[2][4]），可以将 dis[4]的值从 ∞ 松弛为 4（dis[4]初始为 ∞，dis[2]+e[2][4]=1+3=4，dis[4]>dis[2]+e[2][4]，因此 dis[4]要更新为 4）。
刚才我们对 2 号顶点所有的出边进行了松弛。松弛完毕之后 dis 数组为：
接下来，继续在剩下的 3、4、5 和 6 号顶点中，选出离 1 号顶点最近的顶点。通过上面更新过 dis 数组，当前离 1 号顶点最近是 4 号顶点。此时，dis[4]的值已经从“估计值”变为了“确定值”。下面继续对 4 号顶点的所有出边（4->3，4->5 和 4->6）用刚才的方法进行松弛。松弛完毕之后 dis 数组为：
继续在剩下的 3、5 和 6 号顶点中，选出离 1 号顶点最近的顶点，这次选择 3 号顶点。此时，dis[3]的值已经从“估计值”变为了“确定值”。对 3 号顶点的所有出边（3->5）进行松弛。松弛完毕之后 dis 数组为：
继续在剩下的 5 和 6 号顶点中，选出离 1 号顶点最近的顶点，这次选择 5 号顶点。此时，dis[5]的值已经从“估计值”变为了“确定值”。对5号顶点的所有出边（5->4）进行松弛。松弛完毕之后 dis 数组为：
最后对 6 号顶点所有点出边进行松弛。因为这个例子中 6 号顶点没有出边，因此不用处理。到此，dis 数组中所有的值都已经从“估计值”变为了“确定值”。
最终 dis 数组如下，这便是 1 号顶点到其余各个顶点的最短路径。
OK，现在来总结一下刚才的算法。算法的基本思想是：
每次在不确定的最短路中找到离源点最近的一个顶点，然后以该顶点为中心进行更新，最终得到源点到其余所有点的最短路径。
基本步骤如下：
- 将所有的顶点分为两部分：已知最短路程的顶点集合 P 和未知最短路径的顶点集合 Q。最开始，已知最短路径的顶点集合 P 中只有源点一个顶点。我们这里用一个 b[ i ]数组来记录哪些点在集合 P 中。例如对于某个顶点 i，如果 book[ i ]为 1 则表示这个顶点在集合 P 中，如果 b[ i ]为 0 则表示这个顶点在集合 Q 中。
- dis[ i ] 来存储 1 号顶点到其余各个顶点的初始路程。设置源点 s 到自己的最短路径为 0 即 dis=0。若存在源点有能直接到达的顶点 i，则把 dis[ i ]设为 a[s][ i ]。同时把所有其它（源点不能直接到达的）顶点的最短路径为设为 ∞。
- 在集合 Q 的所有顶点中选择一个离源点 s 最近的顶点 u（即 dis[u]最小）加入到集合 P。并考察所有以点 u 为起点的边，对每一条边进行松弛操作。例如存在一条从 u 到 v 的边，那么可以通过将边 u->v 添加到尾部来拓展一条从 s 到 v 的路径，这条路径的长度是 dis[u]+a[u][v]。如果dis[u]+a[u][v]比目前已知的 dis[v]的值要小，我们可以用dis[u]+a[u][v]来替代当前 dis[v]中的值。
- 重复第 3 步，如果集合 Q 为空，算法结束。最终 dis 数组中的值就是源点到所有顶点的最短路径。
#include
#include
#include
#include
#include
#include
using namespace std;
int num=0;
int head[500005]={0},nxt[500005]={0},to[500005]={0},v[500005]={0};
int n,m,k;
int b[10005]={0};//是否出队
priority_queue< pair > q; //一维 d的相反数 二维 编号
int d[10005]={0}; //最短路
void add(int x,int y,int z)
{
nxt[++num]=head[x]; //head（x点连的第一条边）
head[x]=num; //nxt （一条边后的另一条边）
to[num]=y;
v[num]=z;
}
void dj() //边非负
{
for(int i=1;i<=n;i++) d[i]=2147483647; d[k]=0;
memset(b,0,sizeof(b));
q.push(make_pair(0,k)); //出现疑似最短路入队
while(!q.empty())//出队最短路已确定
{
int x=q.top().second; q.pop(); //找最小
if(b[x]) continue; b[x]=1; //标记
for(int i=head[x];i;i=nxt[i]) //用最小更新
{
int y=to[i];
if(d[y]>d[x]+v[i])
{
d[y]=d[x]+v[i];
q.push(make_pair(-d[y],y));
}
}
}
}
int main()
{
scanf("%d%d%d",&n,&m,&k);
int x,y,z;
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
//add(y,x,z); //无向图
}
dj();
for(int i=1;i<=n;i++)
printf("%d ",d[i]);
return 0;
} spfa
类似的，我们用数组d记录每个结点的最短路径估计值，而且用邻接表来存储图G。
我们采取的方法是动态逼近法：设立一个先进先出的队列q[ ]用来保存待优化的结点，优化时每次取出队首结点u，并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作，如果v点的最短路径估计值有所调整，且v点不在当前的队列中，就将v点放入队尾，如果在队列中可以直接更该。（注意 优先队列不行，只能重新加入； dj中q 是优先队列，spfa中q是单纯的队列；）
这样不断从队列中取出结点来进行松弛操作，直至队列空为止，队空时表示所有的边都满足“三角形”法则。
（注意 dj 中的b表示出没出队，spfa中的b表示是否在队中）
（注意 dj 由于每次找最短边，只要出队了就找到了最短路 ；而spfa没有找最短边，所可能需要多次入队出队）
#include
#include
#include
#include
#include
#include
using namespace std;
int n,m,s;
int head[500005]={0},nxt[500005]={0},to[500005]={0},v[500005]={0};
int num=0;
int l=1,r=0;
int b[100005]={0},q[100005]={0};
int d[100005]={0};
void add(int x,int y,int z)
{
nxt[++num]=head[x];
head[x]=num;
to[num]=y;
v[num]=z;
}
void spfa()
{
memset(b,0,sizeof(b)); b[s]=1;
for(int i=1;i<=n;i++) d[i]=2147483647; d[s]=0;
q[++r]=s;
while(l<=r)
{
int x=q[l++]; b[x]=0;
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
if(d[y]>d[x]+v[i])
{
d[y]=d[x]+v[i];
if(b[y]==0) b[y]=1,q[++r]=y;
}
}
}
return;
}
int main()
{
scanf("%d%d%d",&n,&m,&s);
for(int i=1;i<=m;i++)
{
int x,y,v;
scanf("%d%d%d",&x,&y,&v);
add(x,y,v);
}
spfa();
for(int i=1;i<=n;i++) printf("%d ",d[i]);
return 0;
}
时间复杂度
1.dj O( (m+n)log n )
2.spfa O( mn )