非局部均值滤波算法
#####2016.09.09更新,修改了SSIM中值太大的问题
首先谈一下什么是非局部均值滤波。在此之前,我们先来看一下均值滤波的原理。
#####均值滤波
均值滤波的计算非常简单,将图像像素点灰度记录在数组中,然后设置方框半径的值,然后将方框中的所有点的像素求和取平均,得到的结果就是均值滤波后对应像素点的灰度值。
优点:
计算很快而且简单
从算法可以看出,只是求了平均,并没有很复杂的计算
缺点:
得到的图像很模糊
当方框的半径越大,得到的图像中那些变化较大的地方(边缘)计算后变化就越小,即边缘不明显,即模糊
#####非局部均值滤波
非局部均值滤波的基本原理与均值滤波类似,都是要取平均值,但是非局部均值滤波在计算中加入了每一个点的权重值,所以能够保证在相邻且相差很大的点在方框中求平均值时相互之间的影响减小,也就对图像边缘细节部分保留很多,这样图像看起来会更清晰。非局部均值滤波的算法我认为可以大致分为以下几个步骤:
- 首先在一个点A周围取一个大的框(搜索框),设边长为s,A在方框的中心,然后再在方框中取小的方框,即相似框,设边长为d
- 那么在A周围也有一个边长为d的方框,然后在大方框中找到所有边长为d的小方框的组合(就是一个小正方形在一个大正方形中到处移动,记录小正方形中心点的坐标就行了),设小方框的中心点为B,分别于A周围的相似框求减法,并且加入高斯核计算得到的加权值,这样可以计算出一个二维数组,里面存放着各个点的差值乘以权重后的值,加入高斯核主要是因为距离中心点距离不同对中心点的影响大小也不同,而且高斯核的权重和是1,所以就不用再归一化了。
- 然后将这个二维数组求和并平均,得到的值就是这个相似框的中心点B对于A的权重值。计算出A周围所有点的权重值,其实这个时候这个值和权重是成反比的,以A本身为例(以A为中心点的相似框),计算出来A对于A的所谓权重值是零。然后根据计算出来的值用一个指数减函数就得到了成正比的权重关系,具体的函数见下面的代码,w=exp(-d/h),就是这个,其中d就是计算出来的值啦,代入后w就是成正比的权重关系啦,h是一个滤波百分比值。可以先固定为一个常数。 而且这个计算出来w就是一个(0,1)的值哦,自动归一化啦
- 然后就是根据得到的权重值以及各个点本身的灰度值计算出非局部均值滤波后A点的灰度值。
- 以此类推,可以计算出图中所有点经过非局部均值滤波后的值
优点
可以既去除噪声,又保留图像边缘细节
当然去噪声指的一般是高斯白噪声,因为高斯白噪声的均值是0,所以求和取平均会比较有效果
缺点
计算起来很慢
如果图像像素点比较多,而且计算的时候取的框还比较大的话,那么计算一般几分钟是要的了。
下面是一段非局部均值滤波的代码:
function [output]=NLmeansfilter(input,t,f,h)
[m n]=size(input);
%t:搜索框半径;f:相似框半径;h:滤波频率百分比
Output=zeros(m,n);
input2 = padarray(input,[f f],'symmetric');
%将边缘对称折叠上去
% f :加宽的宽度值
kernel = make_kernel(f); %计算得到一个高斯核,用于后续的计算
kernel = kernel / sum(sum(kernel)); %sum:对矩阵k的每一列求和,k表示矩阵k的总和
h=h*h;
for i=1:m
for j=1:n
i1 = i+ f;
j1 = j+ f;
W1= input2(i1-f:i1+f , j1-f:j1+f);
wmax=0;
average=0;
sweight=0;
rmin = max(i1-t,f+1); %确定相似框的边长,其实可以在代入数据的时候就设置搜索框和边界框边长的大小关系,就不用求最大最小值了
rmax = min(i1+t,m+f); %这段主要是控制不超出索引值
smin = max(j1-t,f+1);
smax = min(j1+t,n+f);
for r=rmin:1:rmax
for s=smin:1:smax
if(r==i1 && s==j1) continue; end;
W2= input2(r-f:r+f , s-f:s+f);
d = sum(sum(kernel.*(W1-W2).*(W1-W2)));
w=exp(-d/h);
if w>wmax
wmax=w;
end
sweight = sweight + w;
average = average + w*input2(r,s);
end
end
average = average + wmax*input2(i1,j1);
sweight = sweight + wmax;
if sweight > 0
output(i,j) = average / sweight;
else
output(i,j) = input(i,j);
end
end
end
function [kernel] = make_kernel(f) %这是一个高斯核
kernel=zeros(2*f+1,2*f+1);
for d=1:f
value= 1 / (2*d+1)^2 ;
for i=-d:d
for j=-d:d
kernel(f+1-i,f+1-j)= kernel(f+1-i,f+1-j) + value ;
end
end
end
kernel = kernel ./ f;
#####2016.08.09更新
这次主要更新一下图像去噪的两个评价标准:PSNR和SSIM
#####PSNR
峰值信噪比,主要用来评价算法的去噪能力,计算公式如下:
PSNR=10log10(2n−1)2MSE=20log202n−1MSEPSNR=10log_{10}\frac{(2^n-1)^2}{MSE}=20log_{20}\frac{2^n-1}{\sqrt{MSE}}PSNR=10log10MSE(2n−1)2=20log20MSE2n−1
其中MSE表示原始图像和去噪图像的均方误差
MSE=1mn∑i=1m∑j=1n∥I(i,j)−K(i,j)∥2MSE=\frac{1}{mn}\sum_{i=1}^m\sum_{j=1}^n\|I(i,j)-K(i,j)\|^2MSE=mn1i=1∑mj=1∑n∥I(i,j)−K(i,j)∥2
其中m和n分别表示图像的长和宽,I和K分别表示原图和去噪后的图
从公式可以看出,PSNR的值越大,表示去噪的效果越好
求PSNR的代码如下:
function PSNR=PSNR_work(I,In)
%I:滤波后的图像,In:加噪声后的图像
I=im2double(I);
In=im2double(In);
[m,n]=size(I);
MSE=0;
for i=1:m
for j=1:n
MSE=MSE+(I(i,j)-In(i,j))*(I(i,j)-In(i,j));
end
end
MSE=sqrt(MSE/(m*n));
MAX=1; %特指8位的灰度图 2^8-1=255,在matlab中归一化后取1
PSNR=20*log10(MAX/MSE);
end
代码中没有考虑到I和In大小不同的情况,所以当出现大小不同时,求出来的值没有意义
#####SSIM
结构相似性,用来判断两幅图像的相似性程度的,也可以作为判断去噪效果的评价指标,计算公式如下:
SSIM(X,Y)=(2μxμy+C1)(2σXσY+C2)(σXY2+C3)(μX2+μY2+C1)(σX2+σY2+C2)(σXσY+C3)SSIM(X,Y)=\frac{(2\mu_x\mu_y+C_1)(2\sigma_X\sigma_Y+C_2)(\sigma_{XY}^2+C_3)}{(\mu_X^2+\mu_Y^2+C_1)(\sigma_X^2+\sigma_Y^2+C_2)(\sigma_X\sigma_Y+C_3)}SSIM(X,Y)=(μX2+μY2+C1)(σX2+σY2+C2)(σXσY+C3)(2μxμy+C1)(2σXσY+C2)(σXY2+C3)
或者
SSIM(X,Y)=(2μXμY+C1)(2σXY2+C2)(μX2+μY2+C1)(σX2+σY2+C2)SSIM(X,Y)=\frac{(2\mu_X\mu_Y+C_1)(2\sigma_{XY}^2+C_2)}{(\mu_X^2+\mu_Y^2+C_1)(\sigma_X^2+\sigma_Y^2+C_2)}SSIM(X,Y)=(μX2+μY2+C1)(σX2+σY2+C2)(2μXμY+C1)(2σXY2+C2)
两个公式中的C1=(K1L)2C_1=(K_1L)^2C1=(K1L)2,C2=(K2L)2C_2=(K_2L)^2C2=(K2L)2,第一个公式中的C3=C2/2C_3=C_2/2C3=C2/2
其中,K1=0.01K_1=0.01K1=0.01,K2=0.03K_2=0.03K2=0.03,对于8位的图像来说,L=28−1=255L=2^8-1=255L=28−1=255
两个公式都能表示图像的结构相似性,只是取值范围不同,第一个公式的取值范围在[0,1],第二个公式为[-1,1],两个公式中都是等于1的时候表示两幅图像完全相同
其中平均值和方差的计算公式如下:
μX=1m∗n∑i=1m∑j=1nX(i,j)\mu_X=\frac{1}{m*n}\sum_{i=1}^m \sum_{j=1}^n X(i,j)μX=m∗n1i=1∑mj=1∑nX(i,j)
σX2=1m∗n−1∑i=1m∑j=1n(X(i,j)−μX)2\sigma_X^2=\frac{1}{m*n-1}\sum_{i=1}^m \sum_{j=1}^n (X(i,j)-\mu_X)^2σX2=m∗n−11i=1∑mj=1∑n(X(i,j)−μX)2
σXY2=1m∗n−1∑i=1m∑j=1n(X(i,j)−μX)(Y(i,j)−μY)\sigma_{XY}^2=\frac{1}{m*n-1}\sum_{i=1}^m\sum_{j=1}^n(X(i,j)-\mu_X)(Y(i,j)-\mu_Y)σXY2=m∗n−11i=1∑mj=1∑n(X(i,j)−μX)(Y(i,j)−μY)
计算SSIM的代码如下:
function SSIM=SSIM_work(I,In)
%I:原始图像 In:加了噪声后的图像
I=im2double(I);In=im2double(In);
miu_x=0;miu_y=0;
%miu_x:I的平均值 miu_y:In的平均值
sigma_x=0;sigma_y=0;sigma_xy=0;
%sigma_x:I的方差 sigma_y:In的方差 sigma_xy:I和In的协方差
k1=0.01;k2=0.03;
L=1; %在MATLAB中由于对灰度值的归一化所以这里取1
c1=(k1*L)*(k1*L);c2=(k2*L)*(k2*L);c3=c2/2;
%c1:用来维持稳定的常数 c2:用来维持稳定的常数
[m,n]=size(I);
for i=1:m
for j=1:n
miu_x=miu_x+I(i,j);
miu_y=miu_y+In(i,j);
end
end
miu_x=miu_x/(m*n);
miu_y=miu_y/(m*n);
for k=1:m
for l=1:n
sigma_x=sigma_x+(I(k,l)-miu_x)^2;
sigma_y=sigma_y+(In(k,l)-miu_y)^2;
sigma_xy=sigma_xy+(I(k,l)-miu_x)*(In(k,l)-miu_y);
end
end
sigma_x=sigma_x/(m*n-1);sigma_y=sigma_y/(m*n-1);
sigma_xy=sigma_xy/(m*n-1);
sigma_x=sqrt(sigma_x);sigma_y=sqrt(sigma_y);
%sigma_xy=sqrt(sigma_xy);
l_xy=(2*miu_x*miu_y+c1)/(miu_x^2+miu_y^2+c1);
c_xy=(2*sigma_x*sigma_y+c2)/(sigma_x^2+sigma_y^2+c2);
s_xy=(sigma_xy*sigma_xy+c3)/(sigma_x*sigma_y+c3);
SSIM=l_xy*c_xy*s_xy;
%SSIM=(2*miu_x*miu_y+c1)*(2*sqrt(sigma_xy)+c2)/((miu_x^2+miu_y^2+c1)*(sigma_x+sigma_y+c2));
end
这样,用PSNR和SSIM就能评价非局部均值的去噪能力了,当然,还是需要一个对比来显示出非局部均值算法的去噪能力,这里先写了一个简单的均值滤波,代码如下:
function [Im]=Average_Filter(I,r)
%I:原始图像 r:框半径
In=padarray(I,[r,r],'symmetric');
In=im2double(In);
[m,n]=size(I);
Im=zeros(m,n);
for i=1:m
for j=1:n
c_i=i+r;
c_j=j+r;
sum=0;
for k=c_i-r:1:c_i+r
for l=c_j-r:1:c_j+r;
sum=sum+In(k,l);
end
end
sum=sum/(2*r+1)^2;
if sum>0
Im(i,j)=sum;
else
Im(i,j)=I(i,j);
end
end
end
得到的实验结果如下:
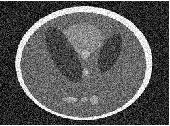
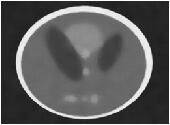
三幅图分别为原始图像,加了方差为0.01的高斯白噪声后的图像和非局部均值滤波后的图像,用评价指标评价的结果如下:
噪声图像:PSNR–>20.3265,SSIM–>0.9156
滤波图像:PSNR–>31.0105,SSIM–>0.9924
从图像和数据上可以看出,滤波后的图像噪点减少很多,清晰度有所下降,图像整体观感提升很多