【编译原理龙书笔记】（三）词法分析（附联系答案）（仍未完成）

这篇博客是根据自己学习龙书的过程编写，因为博主习惯了英语环境，在强行从英语转化为中文的时候难免会有些不自然，请大家谅解。

配套的练习题答案可以在 https://github.com/Oh233/Dragon_book_exercise 看到。

感谢沉鱼姐姐，很多答案都是参考了她的github，虽然无缘认识，但也算是一位领路人。

---

3.1 词法分析器的作用

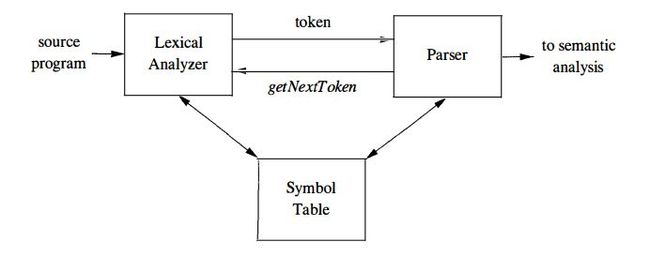
词法分析是编译的第一阶段。

词法分析器读取了源程序，将其打碎成一个个的token之后传入语法分析器。

词法分析器的任务：

• 读取源程序，过滤掉源程序的注释和空白。
• 将编译器生成的错误信息与源程序的位置联系起来。
• 宏的扩展
• 生成词法单元

3.1.1 词法分析及语法分析

我们将词法分析和语法分析分离开并不是毫无根据的。至少有以下几个好处：

1. 简化编译器的设计。如果在语法分析阶段，仍旧要考虑什么过滤注释，过滤空白之类的鬼东西，设计起来简直可以杀了程序员。于是我们选择将两部分分开。这种思想在软件工程的设计中十分常见，包括在计算机网络的层结构中也可以看到。
2. 提高编译器的效率。
3. 增强编译器的可移植性。有的时候输入的字符会跟设备有关，这样的情况下，我们只需要改一改其中一小部分的词法分析，就可以得到适应机器的结果，而非要修改整个词法分析+语法分析。

3.1.2 词法单元，模式，词素

这三者读起来很相似然而概念上却是完全不同的东西。

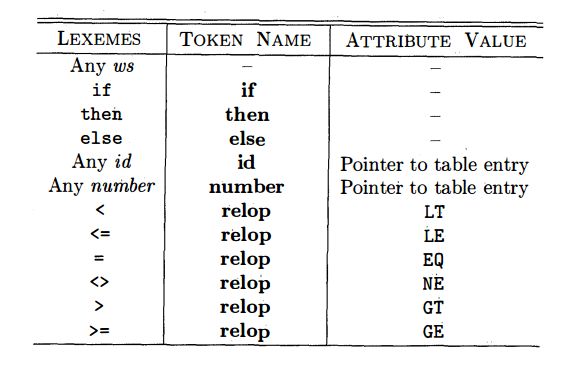
• 词法单元是由一个词法单元名和一个（可选的）属性值组成。词法单元名是一个表示某种词法单位的抽象符号。
• 模式描述了一个词法单元的词素可能具有的形式。当词法单元是一个关键字时，它的模式就是组成这个关键字的字符序列。对于标识符和其他词法单元，模式就是一个更加复杂的结构，可以和很多字符串匹配。
• 词素是源程序的一个字符序列，和某个词法单元的模式匹配，会被词法分析器识别为某个词法单元的一个实例。

在绝大多数的程序设计语言中，词法单元由五大部分组成：

1. 关键字。关键字的模式就是关键字本身
2. 运算符。这些运算符既可以是单个的运算符，也可以是代指一类运算符（比如比较运算符）
3. 表示所有标识符的词法单元。初学者可以把其理解成存储各种变量名的地方。
4. 一个或多个表示常量的词法单元，存储了数字和literal字符串
5. 标点符号。左右括号，逗号分号等等。

3.1.3 词法单元的属性

从词法单元的定义来看，就可以看出一个词法单元是可以对应到多个词素的。那么区分这些词素的至关重要的一部分就是给编译器提供词素的额外信息来描述各种不同的词素。

最典型的例子就是在identifier这个词法单元中，其对应的词素包括所有的变量名，那么如何区分这些变量名便成了一个主要的任务。我们通常采用其类型，第一次出现的位置等等去描述它，并把它存储在字符表中。

词法分析的一个大问题就是我们无法在只看一个字符串的时候决定它是对是错，著名的fortran例子告诉我们，有的时候，我们需要看整个statement才能发现这个statement的意思是什么。

3.1.4 词法错误

---

3.2 输入缓冲

之前提到过，在大部分程序中，我们都需要有 look ahead 情景的出现，这就给读入过程增加了复杂性。“我们一次到底该读多少代码呢”，这一节我们就会介绍这些问题。

3.2.1 缓冲区对

在编译一个程序的时候，我们往往需要进行大量的字符串读入。前人做了比较多的优化，其中一项就是采用来个交替读入的缓冲区。每个缓冲区大概能有4096的字节，如果不是疯狂搞破坏的话读一句话肯定够了（不够的情况后文也有解释）。

读入程序中维护了两个指针：分别是

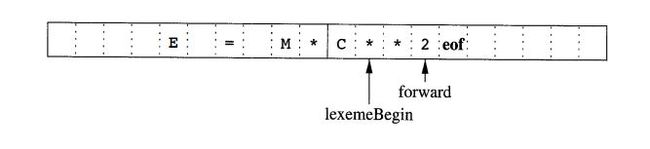
1. lexemeBegin 指针，顾名思义，就是当前词素的开始处。
2. forward 指针，就是试图判断词素的结尾是什么。这个很复杂我们会在接下来的章节中详细介绍。

可以想象，一旦确定了当前词素的位置，那我们就把forward的位置+1之后赋值给lexemeBegin，然后继续上述的过程。

但是简单地做上面的工作会有一个小小的问题，就是如果恰好一个词素被分开了怎么办，这就涉及到了哨兵标记。

3.2.2 哨兵标记

主要就是说，当我们移动forward指针的时候，实际上我们同时做了两件事情，第一件事情是判断是否已经能够完成词素的匹配。并且要同时检查我们是否到了缓冲区的结尾（如果到了结尾自然要选择是不是要重新装载缓冲区，是不是要大幅度移动forward指针），这个问题被 eof 很好的解决了。我们在这里描述一种处理这个问题的算法，这个算法十分清晰，让人一目了然。

switch (*forward++) {
    case eof:
        if (forward = buff1.end()) {
            load buff2;
            forward = buff2.begin();
        }
        else if (forward = buff2.end()) {
            load buff1;
            forward = buff1.begin();
        }
        else terminate lexical analysis; // This is end of whole code
    case otherWords:
}

在现代编程语言中，词素的长度往往并没有那么长，然而如果你硬要问我有没有无敌长的字符串，其实还是有的。在这种情况下，我们会采用一些算法，将其视为多个不是很长的字符串的加和，之后的处理中再把他们加和起来。

一种更加严重的情况就是当我们需要往前看很多很多字符才能决定词素的情况。在曾经的PL/I语言中，关键字并不是保留字。曾经出现过 DECLARE (ARG1, ARG2, … , ARGN) 此般凶残的杀人法。我们无法判断 DECLARE到底是一个关键字，还是一个数组的名字，在当时，只能做两个分支，然后由语法分析器来解决这个问题，不过现在的绝大多数编程语言都将关键字保留，以避免这类愚蠢的问题。

3.3 词法单元的规约

书中提到，正则表达式是一种用来描述词素模式的重要方法，虽然我并不能懂这句话的意思，但是让我们先走入正则表达式的世界，去一窥究竟。

3.3.1 串和语言

这一节中给出了我们所需要语言的一些定义。首先，字母表（alphabet）是一个有限的符号集合，我们后面所定义的语言，表达式等等东西都要依靠于这个字母表。

某个字母表上的一个字符串（string）是该字母表中符号的又穷序列。注意这个串可以是空的，我们用 ϵ 来表示。

串的前缀就是从其尾部删除一些符号得到的串，对应来说后缀就是从其头部删除一些符号得到的串。之后串的子串是删除某个前缀加上删除某个后缀后得到的串。

因为前缀和后缀其实可能是串本身，所以我们规定串的真前缀和真后缀，即是非本身的前后缀串。

3.3.2 语言上的运算

这一节又给出了一些繁琐的集合论的定义。大意就是给出字母表集合的时候，其上的并（union），连接（concatenation），闭包的定义。因为跟代数中的形式过于相近，这里就先不给出其表格形式了。

3.3.3 正则表达式

正则表达式实际上是用于描述一套字符串集合所定义的一套语法。我们用特定的字符串加上一些符号去描述我们想描述的一些具有某些性质的字符串。

那么我们为什么需要正则表达式呢，大概是因为在描述一些数量庞大的字符串集合的时候，应用正则表达式的概念，会让我们的描述更加清晰。

同时，我们不会想要每次都强行的写出所有正则表达式的字母表示形式，因此我们开发了递归这种东西。下面给出正则表达式递归式的明确定义。

归纳基础：

1) ϵ 是一个正则表达式，其所对应的语言 L(ϵ)={ϵ}，是一个只有空字符的语言。
2) 如果a是∑上的一个符号，那么a也是一个正则表达式，L(a)={a}。就是说只有一个字符的语言。

归纳部分：

1) (r) | (s) 是一个正则表达式，其所对应的语言为 L(r)∪L(s)
2) (r) (s) 是一个正则表达式，其所对应的语言为 L(r)L(s)
3) (r)* 是一个正则表达式，其所对应的语言为 (L(r))∗
4) (r) 是一个正则表达式，只是说明在表达式左右加个括号是没有影响的。】

3.3.4 正则定义

其实关于正则定义的应用，我们在第二章的时候应该已经看过一点了。正则定义出现的意义主要是因为为了简化定义式的表达。举个例子好了，当我们要用正则表达式定义C语言中所有可能出现的标识符的名字的时候：

letter_→A|B|⋯Z|a|b|⋯|z|_digit→0|1|⋯|9id→letter_(letter_|digit)∗

上述的id定义中我们用到了之前所定义的letter_ 和 digit，这就是正则定义的简化之处。

如果形式化地定义以上的结果，我们对正则定义有如下的写法：

d1→r1d2→r2⋯dn→rn

其中的ri 就不只用了字符表中的定义，还有之前 di−1的定义。我们管这样的定义序列叫做正则定义。

3.3.5 正则表达式的扩展

OK到了这里正则表达式的东西基本都介绍完了，但是程序员们是一些不会满足的人。因此大家又定义了一些其他的符号，我们一起来看一下：

1. ＋，表示一个或多个实例。
2. ? ，表示零个或一个实例。
3. 字符类，当我们想表示 a|b|⋯|z的时候，我们可以简单的用［a-z］去表达。这样简化了很多我们所需要的工作。

---

3.4 词法单元的识别

上一节中，我们介绍了关于正则表达式的一些东西，然而如果不配合上一些应用的话，会给人一种“这并没有什么鸟用的感觉“。那在接下来的章节中，我们就即将说明，这正则表达式还是有些鸟用的。

好了，那假如我们现在心血来潮想要搞出一门编程语言，也许就叫 C减减。然后其control flow是如下图所示的。if then都是保留字，relop是比较符号。

那么我们就可以设置对应的正则表达式语言为下图

还记得吗，词法分析器还有一个职责就是过滤所有的空白符号，包括空格，tab符号和回车键。那么我们还要设计关于空白符号的正则表达式。

我们所想要的目标如下图所示，当我们检测到id或者number的话，我们就会去符号表中去找所对应的entry。而当我们遇到关系运算符的时候，会直接设置所对应词素的属性。

那我们要如何进行识别呢，这就是我们下面要介绍的状态转换图了。

3.4.1 状态转换图

首先介绍一下基本概念，状态转换图是我们构建词法分析器的一个中间步骤。我们想要的是根据语法的正则表达式来构建一个模式转换图。图中每一个节点代表我们词法分析的一个中间状态，随着读入输入的字符串而不停变化，一般来说，从读入第一个字符串开始，在遇到whitespace之后停止。

有一些关于状态转换的约定，都是很直观的东西，在这里列出来权当备注。

1) 接受状态或最终状态：这些状态表明我们又找到了一个词素，在状态转换图中经常用双层的圈来表示。
2) 如果需要将forward指针往前退一个位置，那我们就在途中的节点旁边加上一个星号。
3) 必须要有一个状态被指定为开始状态。一般这个状态都是在刚读完一个词素，要开始读下一个词素的时候。

下面是一个例子，是我们读入关系运算符的时候，所做的状态转换。

这张图很好懂，无非就是根据读了什么走不同的状态，这里也不多赘述。

3.4.2 保留字和标识符的识别

这是一个关键的问题，试想一下，当你有一个变量名字叫做thennext的时候，这时候我们的程序一个一个字符的往后读，读到then的时候词法分析器就会觉得日了狗了，不知道是关键字还是只是一个变量名。

我们解决这个问题的最好方法在之后有介绍，就是把所有状态转换图并到一个，这样编译器就能用很多switch语句分别处理而不用纠结，但是这样当然会带来的问题就是实现的复杂会成倍地提高，不过仍然是值得的。我们之后会采取那种方法，所以现在书中介绍的治标不治本的方法这里也不介绍了。

3.4.3 完成我们的例子

我们没有做的地方还有读入数位的例子，那个图虽然长，然而并没有什么意义，其实就是一些非常暴力的实现。

3.4.4 基于状态转换图的词法分析器的体系结构

无论我们要采用什么奇技淫巧，如果我们的词法分析器是基于状态转换图而建立的，我们永远都可以把图中的一个结点当做是一个状态，然后用switch语句去转换状态（对应转换图中的每一条边）。多说无用，直接看我们的代码吧，看了就都明白了。

TOKEN getRelop()
{
    TOKEN retToken = new(RELOP);
    while (1) {
        switch(state) {
            case 0: c = nextChar();
                    if (c == '<') state = 1;
                    else if (c == '=') state = 5;
                    else if (c == '>') state = 6;
                    else fail();
                    break;
            case 1: ...
            ...
            case 8: retract();
                    retToken.attribute = GT;
                    return(retToken);
        }
    }
}

上图中的retract的含义是因为我们读取了多一个字符，然后需要把指针向前移动一位，所以才要考 retract 函数来完成。

---

照例自我介绍：

ID: Oh2 / Oh233
github: http://github.com/oh233
csdn: http://blog.csdn.net/oh233
个人网站: http://oh233.com
知乎: http://www.zhihu.com/people/qi-hao-zhi-65