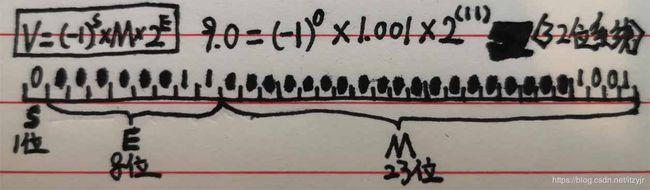关于C之整数与浮点数二进制表示

先看看整数的二进制表示

关于字节与位：

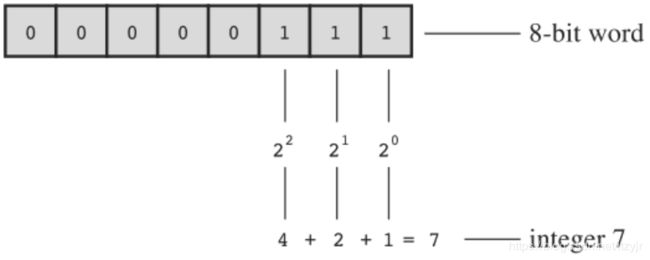
一个int占4个字节(byte)，一个字节占8位(bit)，所以一个int占用4x8=32位。

char类型的范围为什么是-128~127？

有一个整型范围的公式：-2^(n-1)~2^(n-1)-1 (n为整型的内存占用位数)。

对于char类型，占一个字节，n=8，代入得：-128~127。

char占8位，用二进制表示为 0000 0000 ~ 1111 1111，1111 1111最大即为十进制255，所以 unsigned char 的范围为0~ 255。

但是对于有符号整数，二进制的最高位表示正负，不表示数值，最高位为 0 时表示正数，为 1 时表示负数，这样一来，能表示数值的就剩下( n-1 )位了，比如 char a = -1;   那么二进制表示就为 1 0000001，1 表示为 0 0000001，所以 signed char 型除去符号位剩下的 7 位最大为 1111 111 = 127，再把符号加上，0 1111111 = 127，1 1111111 = -127，范围应该为 -127~127。

但会有问题出现：

先看1+1=？

  0000 0001
+ 0000 0001
———————————
  0000 0010 ……………… 2 运算正确

再看1-1=?，由于计算机只会加法不会减法，它会转化为1+(-1)=?

  0000 0001
+ 1000 0001
___________
  1000 0010 …………… -2 运算错误

1-1 = -2?  这显然是不对了，所以为了避免减法运算错误，计算机大神们发明出了反码，直接用最高位表示符号位的叫做原码， 上面提到的二进制都是原码形式，反码是原码除最高位其余位取反，规定：正数的反码是其本身，负数的反码是原码除了符号位，其余为都取反。现在再用反码来计算 1+(-1) ：

  0000 0001
+ 1111 1110
————————————
  1111 1111 ………… 再转化为原码就是 1000 0000 = -0  

虽然反码解决了相减的问题，却又带来一个问题：-0 ，既然 0000 0000 表示 0，那么就没有 -0 的必要， 出现 +0 = -0 = 0 ，一个 0 就够了，为了避免两个 0 的问题，计算机大师们又发明了【补码】，补码规定： 正数的补码是其本身，负数的补码为其反码加一 ，所以，负数转化为补码需两个步骤：第一，先转化为反码；第二， 把反码加一。

---

正数的反码、补码都是本身；负数的反码=除符号位都取反、负数的补码=反码+1。

记：反码与补码是针对负数而发明的，所以正数反码、补码就是本身。对负数：“反”码，即(除符号位)都取“反”；“补”码，即“补”一位(+1)。

---

这样1+(-1) ：

  0000 0001
+ 1111 1111
___________
1 0000 0000 ……………………  由于 char 为 8 位，最高位 1 被丢弃结果为 0 ，运算正确。

-0 ：原码 1000 0000 的补码为 1 0000 0000 ，由于 char 是 八位 ，所以取低八位 0000 0000。   
+0 ：原码 0000 0000 ，补码为也为 0000 0000 ，虽然补码 0 都是相同的，但是有两个 0 ，既然有两个 0 ，况且 0 既不是正数，也不是负数， 用原码为 0000 0000 表示就行了。

这样一来，有符号的 char，原码都用来表示 -127~127 之间的数了，唯独剩下原码 1000 0000 没有用。1000 0000作为负数，反码:1111 1111，补码为:1111 1111 + 0000 0001 = 1 0000 0000（最高位1表示负数，后面8位，2^7=128，则表示-128）

-128 的原码和 -0(1000 0000) 的原码相同吗？答：是不同的。但是在 char 型中，是可以用 1000 0000 表示 -128 的，关键在于char 是 8 位，它把 -128 的最高位符号位 1 丢弃了，截断后 -128 的原码为 1000 0000 和 -0 的原码相同，也就是说 1000 0000  和 -128 丢弃最高位后余下的 8 位相同，所以才可以用 -0 表示 -128，这样，当初剩余的 -0(1000 0000)，被拿来表示截断后的 -128，因为即使截断后的 -128 和 char 型范围的其他 (-127~127) 运算也不会影响结果， 所以才敢这么表示 -128。

比如 -128+(-1) ：

  1000 0000   ------------------ 丢弃最高位的-128
+ 1111 1111   ------------------ -1
___________
 10111 1111   ------------------ 用"%c"未打印任何字符,用"%d"打印-129,不过没关系,溢出char型了,当然不能表示了。

比如 -128+127：

  1000 0000
+ 0111 1111
———————————
  1111 1111 ------- -1 结果正确， 所以，这就是为什么能用1000 0000表示-128的原因。

注：1111 1111 ->取原码(逆操作:减一再取反码)=>1000 0001 = -1

---

对于浮点数二进制是怎么表示的呢？

根据国际标准IEEE 754，任意一个二进制浮点数V可以表示成下面的形式：

　　V = (-1)^s×M×2^E
　　（1）(-1)^s表示符号位，当s=0，V为正数；当s=1，V为负数。
　　（2）M表示有效数字，大于等于1，小于2。
　　（3）2^E表示指数位(E是二进制数)。
　　举例来说，十进制的5.0，写成二进制是101.0，相当于1.01×2^2。那么，按照上面V的格式，可以得出s=0，M=1.01，E=2。
　　十进制的-5.0，写成二进制是-101.0，相当于-1.01×2^2。那么，s=1，M=1.01，E=2。
　　IEEE 754规定，对于32位的浮点数，最高的1位是符号位s，接着的8位是指数E，剩下的23位为有效数字M。
　　对于64位的浮点数，最高的1位是符号位s，接着的11位是指数E，剩下的52位为有效数字M。
　　IEEE 754对有效数字M和指数E，还有一些特别规定。
　　前面说过，1≤M<2，也就是说，M可以写成1.xxxxxx的形式，其中xxxxxx表示小数部分。IEEE 754规定，在计算机内部保存M时，默认这个数的第一位总是1，因此可以被舍去，只保存后面的xxxxxx部分。比如保存1.01的时候，只保存01，等到读取的时候，再把第一位的1加上去。这样做的目的，是节省1位有效数字。以32位浮点数为例，留给M只有23位，将第一位的1舍去以后，等于可以保存24位有效数字。
　　至于指数E，情况就比较复杂：
　　➀E为一个无符号整数（unsigned int）。IEEE 754规定，存入内存时E的真实值必须再加上一个中间数，8位的E这个中间数是127；对于11位的E，这个中间1023。这意味着，如果E为8位，它的取值范围为0~255；如果E为11位，它的取值范围为0~2047。

       ➁E为一个有符号整数（int）。IEEE 754规定，存入内存时E的真实值必须再减去一个中间数，对于8位的E，这个中间数是127；对于11位的E，这个中间数是1023。
　　比如，2^10的E是10(此时是10进制表示)，所以保存成32位浮点数时，必须保存成E=10+127=137，即10001001。
　　然后，指数E还可以再分成三种情况：
　　（1）E不全为0或不全为1。这时，浮点数就采用上面的规则表示，即指数E的计算值减去127（或1023），得到真实值，再将有效数字M前加上第一位的1。
　　（2）E全为0。这时，浮点数的指数E等于1-127（或者1-1023），有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数。这样做是为了表示±0，以及接近于0的很小的数字。
　　（3）E全为1。这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位s）；如果有效数字M不全为0，表示这个数不是一个数（NaN）。
　　关于浮点数的表示规则，就到这里。

如float=9.0的内存中表示：

---

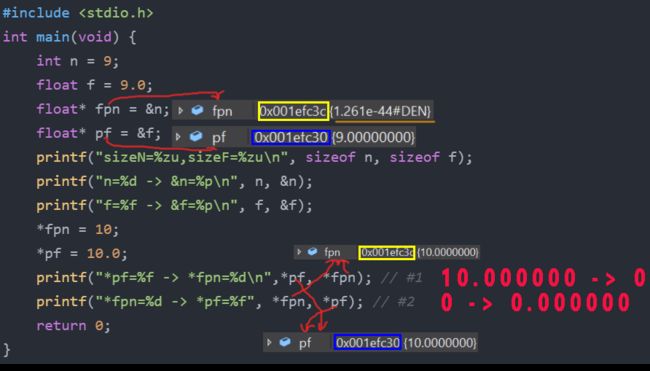
下面num和*pFloat在内存中明明是同一个数，为什么浮点数和整数的解读结果会差别这么大？

#include 
int main(void) {
    int n = 9;
    float f = 9.0;
    float* fpn = &n;
    float* pf = &f;
    printf("sizeN=%zu,sizeF=%zu\n", sizeof n, sizeof f);
    printf("n=%d -> &n=%p\n", n, &n);
    printf("f=%f -> &f=%p\n", f, &f);              
    *fpn = 10;
    *pf = 10.0;
    printf("*pf=%f -> *fpn=%d\n",*pf, *fpn); // #1
    printf("*fpn=%d -> *pf=%f", *fpn, *pf); // #2
    return 0;
}

sizeN=4,sizeF=4
n=9 -> &n=00AFFCCC
f=9.000000 -> &f=00AFFCC0
*pf=10.000000 -> *fpn=0
*fpn=0 -> *pf=0.000000

➊为什么#1行打印的*pf正确，而#2行只是调换了个位置*pf打印却为0?

➋为什么*fpn总打印为0？

断点调试：

从疑问➋开始，整体原因是将float*类型赋值为了int*类型，是不匹配的指针类型赋值操作。通过断点调试发现fpn的地址没变为0x001efc3c，但其表示的值为1.261e-44#DEN，相当于fpn指向的地址是1.261e-44#DEN，所以*fpn不是一个有效地址，1.261e-44#DEN中#DEN是指非规格化数 (denormalized value), 简单来说就是float/double 数字太小了,近乎0的意思

对于疑问➊，把#1和#2行改为如下：

printf("*pf=%f -> *fpn=%f\n",*pf, *fpn); // #1
printf("*fpn=%f -> *pf=%f", *fpn, *pf); // #2
打印输出：
*pf=10.000000 -> *fpn=10.000000
*fpn=10.000000 -> *pf=10.000000

因为fpn这个指针变量声明为float类型，它存储的地址是无效的。其实无论怎样，都应该类型正确的匹配！

看个更简单的例子就更加清晰明白了：

#include 
int main(void) {
    int i = 0x12345678;
    float f = 0x1efc3c;
    double d = 1.79E+38;
    printf("===Wrong===\n");
    printf("%d\n", f);
    printf("%f\n", i);
    printf("%d\n", d);
    printf("===Right===\n");
    printf("%f\n", f);
    printf("%lf\n", d);
    return 0;
}

输出：
===Wrong===
0
0.000000
-1408126465
===Right===
2030652.000000
179000000000000018071044723816240513024.000000

因为int与float/double类型在内存中存储模式是不一样的！

㊀int32的整数0x12345678在内存中对应二进制表示为：

【0】[0010 0100]{011 0100 0101 0110 0111 1000}
第一位符号位0，接下来8位是指数位: 0010 0100, 换算成十进制是: 36。不过浮点数的格式规定，这个数还要减去127才是真正的指数，36 -127 = -91。最后23位是底数位。不过浮点数的格式规定，这个数前面要加上【1.】才是真正的底数，所以底数是1.011 0100 0101 0110 0111 1000。这个数换算成十进制大约是1.40625。最后整个浮点数的值是 1.40625 * 2 ^ -91，计算结果是5.6797985e-28，也就是零点零零零(一共28个零)五六七九七九八五。printf后面的%f只保留6个有效数字，所以就变成0了。

㊁下面来讲一下  float a=7.5f ; printf("%d",a)输出为0的情况：

如果用printf("%d",(float)a)，输出什么，输出的是0，这个只是将a的float类型还转成float类型，还是自动转成doube类型，传给printf函数。
        为什么float非要转成double类型呢，因为printf格式控制浮点型输出只有%f，所以统一按doube类型输出，不像整型有32位的%d或%ld，64位的有%lld，这就将32位整型和64位整型用不同的格式控制分开了，而%f则没有，所以printf输出的浮点数其实是统一遍历了64位内存，如果float传入printf没有进行转换，那么printf输出高32位数据将不可预知，printf输出结果也就不正确了，因此传入printf的浮点数都会被编译器隐含转成double类型。
        %d只输出低32位的数据，并将这些32位二进制以十进制数输出，编译器首先将 7.5从float类型转换为double类型，7.5在内存中的存放方式是0x40f00000，转换成double类型在内存中的数据就是这个0x401e000000000000，这个内存数据可以很明显看出低32位全是0，而%d则只能截取到低32位，所以这个以%d输出7.5的数值当然是 0了。如大家不相信可以用%lld 输出看看，这个%lld就很读到低64位数据，读出的结果就是0x401e000000000000，在屏幕上看到一个很大的十进制数。
        如果我一定要输出7.5在内存中的存放方法怎么办呢？
        可以用printf("%d",*(int *)&a);这里做了一下处理，不是直接把a传进来，把a所在地址里的内容处理了一下，不管a是什么类型，只对地址进行操作，利用（int *）&a，将a所在地址中的内容0x40f00000直接当成 int 类型传给printf，int 的类型数据不会再转成double类型了，所以输出正常，这个只是针对浮点型数据只占低32位，如果输出64位还得用%lld格式控制输出。
        如果用printf("%d",(int)a),输出行不行，这个强制类型转换只针对a的数据类型进行转换，7.5转换 int 类型是7，而上面的*(int *)&a，是对内存中的实际存储数据进行操作，蔽开数据类型这一层面，只将这个数据0x40f00000直接转成int类型输出。而（int）a，要先看a的类型，C语言会根据所要数据类型，对内存存储的数据进行改变，以便可以用int类型正确解析内存数据。

浮点数在计算机内部的表示方法

现代计算机中，一般都以IEEE 754标准存储浮点数，这个标准的在内存中存储的形式为：

对于不同长度的浮点数，阶码与小数位分配的数量不一样，如下：

对于32位的单精度浮点数，数符分配是1位，阶码分配了8位，尾数分配了是23位。

根据这个标准，我们来尝试把一个十进制的浮点数转换为IEEE 754标准表示。

例如：178.125

➀先把浮点数分为整数部分和小数部分转换成2进制。
    整数部分2进制表示：10110010
    小数部分2进制表示：001（0×2^-1+0×2^-2+1×2^-3=0.125）
    合起来即是：10110010.001
    转换成二进制的浮点数，即把小数点移动到整数位只有1，即为：1.0110010001 * 2^111，111是二进制，由于左移了7即二进制111
➁把浮点数转换二进制后，这里基本已经可以得出对应3部分的值了。
    数符：由于浮点数是正数，故为0(负数为1)
    阶码 : 阶码的计算公式：阶数 + 偏移量,  阶码是需要作移码运算，在转换出来的二进制数里，阶数是111(十进制为7)，对于单精度的浮点数，偏移值为01111111(127)[偏移量的计算是：2^(n-1)-1, n为阶码的位数，即为8，因此偏移值是127]，即：111+01111111 = 10000110
    尾数：小数点后面的数，即0110010001
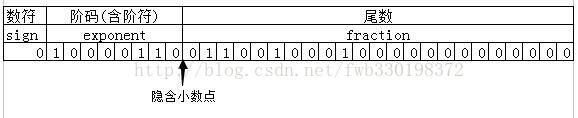
    最终根据位置填到对位的位置上：

小数点前面的1去哪里了？由于尾数部分是规格化表示的，最高位总是“1”，所以这是直接隐藏掉，同时也节省了1个位出来存储小数，提高精度。

---

       ➊为什么9还原成浮点数，就成了0.000000？
　　首先，9对应二进制为0000 0000 0000 0000 0000 0000 0000 1001，和上图对比，符号位s=0，E=0000 0000，最后23位的有效数字M=000 0000 0000 0000 0000 1001。
　　由于指数E全为0，所以符合上面的第（2）种情况。因此，浮点数V就写成：
　　V=(-1)^0×0.00000000000000000001001×2^(-126)=1.001×2^(-146)
　　显然，V是一个很小的接近于0的正数，所以用十进制小数表示就是0.000000。

---

       ➋浮点数9.0，如何用二进制表示？还原成十进制又是多少？
　　首先，浮点数9.0等于二进制的1001.0，即1.001×2^11（11为二进制）。
　　那么，第一位的符号位s=0，有效数字M等于001后面再加20个0，凑满23位，指数E等于3+127=130，即10000010。
　　所以，写成二进制形式，应该是s+E+M，即0 10000010 001 0000 0000 0000 0000 0000。这个32位的二进制数，还原成十进制，正是1091567616。