【图论】网络流问题——最大流入门（Dinic算法）

参考文章：
1. 博客园：Dinic算法（研究总结，网络流）
2. 洛谷博客：网络最大流-从入门开始，详细讲到实用易懂的Dinic算法

本文主要是用 Dinic算法 解决最大流问题。

洛谷 P3376 【模板】网络最大流

最大流问题，Dinic算法，最坏时间复杂度为O(V²*E)，然而一般情况下是达不到这么大的，要不这题早超时了。

算法流程
1、根据残量网络计算层次图。
2、在层次图中使用DFS进行增广直到不存在增广路。
3、重复以上步骤直到无法增广。

时间复杂度
因为在Dinic的执行过程中，每次重新分层，汇点所在的层次是严格递增的，而n个点的层次图最多有n层，所以最多重新分层n次。假设总共有m条边，在同一个层次图中，因为每条增广路都有一个瓶颈，而两次增广的瓶颈不可能相同，所以增广路最多m条。搜索每一条增广路时，前进和回溯都最多n次，所以这两者造成的时间复杂度是O(nm)；综上所述，Dinic算法时间复杂度的理论上界是O(n*nm)=O(n²*m)。

简单来说，Dinic算法就是先进行BFS，判断是否有增广路（能从源点s达到汇点t）并且记录图中每个点所在的广度优先搜索生成树的层数，形成分层图；如果有增广路，则进行DFS，限制只能从层数小的向层数大的拓展，如果能找到终点并且返回时流量flow大于0，则每条正向边减去增广路中的最小流量，每条反向边加上增广路中的最小流量（这是算法的关键，引入反向边就是为了“反悔”，或者说“纠正之前可能错误的流量路径”）。

以下的代码，是BFS判断是否有增广路，DFS每次只能搜索出一条增广路。BFS分层之后可以多次循环DFS。

#include 
using namespace std;
//在普通情况下，DINIC算法时间复杂度为O(V^2*E)
const int N=1e4+10,M=1e5+10,inf=1e9;
int n,m,s,t,cnt,head[N],dep[N];
struct edge
{
    int to,w,next;
}e[M<<1];
void add(int x,int y,int z)
{
    e[cnt].to=y;
    e[cnt].w=z;
    e[cnt].next=head[x];
    head[x]=cnt++;
}
void add_edge(int x,int y,int z)
{
    add(x,y,z);
    add(y,x,0);//反向边初始为0
}
bool bfs()
{
    queue<int>q;
    memset(dep,0,sizeof(dep));
    q.push(s);
    dep[s]=1;
    while(!q.empty())
    {
        int u=q.front();q.pop();
        for(int i=head[u];i!=-1;i=e[i].next)
        {
            int v=e[i].to;
            if(e[i].w>0&&dep[v]==0)
            {
                dep[v]=dep[u]+1;
                q.push(v);
            }
        }
    }
    if(dep[t])return 1;
    return 0;
}
int dfs(int u,int flow)
{
    if(u==t)return flow;//到达汇点，返回这条增广路上的最小流量
    for(int i=head[u];i!=-1;i=e[i].next)
    {
        int v=e[i].to;
        if(e[i].w>0&&dep[v]==dep[u]+1)
        {
            int di=dfs(v,min(flow,e[i].w));//min(flow,e[i].w)表示起点到v的最小流量
            if(di>0)//防止dfs结果return 0的情况，如果di=0会死循环
            {
                e[i].w-=di;
                e[i^1].w+=di;//反向边加上di
                return di;//di表示整条增广路上的最小流量，回溯的时候一直向上返回，返回的di是不变的
            }
        }
    }
    return 0;//找不到增广路，到不了汇点
}
int dinic()
{
    int ans=0;
    while(bfs())//先bfs进行“探路”并分层，分层后进行多次dfs
    {
        //每dfs一次，就尝试找到一条增广路并返回路上的最小流量
        while(int d=dfs(s,inf))//while循环的意义：只要dfs不为0，就一直dfs，直到找不到增广路
            ans+=d;
    }
    return ans;
}
int main()
{
    ios::sync_with_stdio(false);
    cin>>n>>m>>s>>t;
    int x,y,z;
    memset(head,-1,sizeof(head));
    for(int i=1;i<=m;i++)
    {
        cin>>x>>y>>z;
        add_edge(x,y,z);
    }
    int ans=dinic();
    printf("%d\n",ans);
    return 0;
}

HDU 4280 Island Transport

模板题，但是Dinic算法需要优化才能过这题。

（1）加边优化：题目是双向边，所以加反向边的时候加的容量直接写成与正向边相同（而不是0），这样每次就只加了2条边。
这个加边优化必须要写。

void add_edge(int x,int y,int z)
{
    add(x,y,z);
    add(y,x,z);//而不是add(y,x,0);
}

（2）优化DFS：

1. 当前弧优化，for(int &i=cur[u];i!=-1;i=e[i].next)
2. 多路增广，不直接返回一条弧的流量，而是把所有弧都跑完或者没有流量后再返回res
3. 炸点，使没有流量(不能再向后流出)的点不会再被访问，标记为dep[u]=-2

//只优化DFS 时间：9516ms
int dfs(int u,int flow)
{
    if(u==t||flow==0)return flow;//到达汇点或者是没有流量，就返回流量
    int res=0;
    for(int &i=cur[u];i!=-1;i=e[i].next)
    {
        int v=e[i].to;
        if(e[i].w>0&&dep[v]==dep[u]+1)
        {
            int di=dfs(v,min(flow,e[i].w));//min(flow,e[i].w)表示起点到v的最小流量
            if(!di)continue;
            e[i].w-=di;
            e[i^1].w+=di;//反向边加上di
            res+=di;//res相当于从v点流出了多少流量(当前的流出流量作为后面点的供给)
            flow-=di;//flow相当于还可以流入多少流量到v点(给当前点的供给)
            //多路增广，不直接返回一条弧的流量，而是把所有弧都跑完或者没有流量后再返回res
            if(flow==0)break;
        }
    }
    if(res==0)dep[u]=-2;//炸点，使没有流量(不能再向后流出)的点不会再被访问
    //不写这句话就会超时！
    return res;
}

（3）还有一种玄学优化，就是优化BFS：在BFS中找到汇点就直接结束。（这个就相当于找到终点就不更新分层图了，我感觉好像有点问题，但是几个OJ测了都没问题）

//只优化BFS 时间：8486ms
bool bfs()
{
    queue<int>q;
    memset(dep,0,sizeof(dep));
    q.push(s);
    dep[s]=1;
    while(!q.empty())
    {
        int u=q.front();q.pop();
        if(u==t)return 1;//这句话非常重要！！！
        for(int i=head[u];i!=-1;i=e[i].next)
        {
            int v=e[i].to;
            if(e[i].w>0&&dep[v]==0)
            {
                dep[v]=dep[u]+1;
                q.push(v);
            }
        }
    }
    if(dep[t])return 1;
    return 0;
}

(4) STL中的queue用数组模拟，能快400ms左右，在这题用处不大。

AC代码：

//BFS,DFS同时优化 未优化STL队列 时间：7675ms
#include 
using namespace std;
const int N=1e5+10,M=1e5+10,inf=0x7f7f7f7f;
int T,n,m,s,t,cnt,head[N],dep[N],cur[N];
struct edge
{
    int to,w,next;
}e[M<<1];
inline void add(int x,int y,int z)
{
    e[cnt].to=y;
    e[cnt].w=z;
    e[cnt].next=head[x];
    head[x]=cnt++;
}
inline void add_edge(int x,int y,int z)
{
    add(x,y,z);
    add(y,x,z);
}
bool bfs()
{
    queue<int>q;
    memset(dep,0,sizeof(dep));
    q.push(s);
    dep[s]=1;
    while(!q.empty())
    {
        int u=q.front();q.pop();
        for(int i=head[u];i!=-1;i=e[i].next)
        {
            int v=e[i].to;
            if(e[i].w>0&&dep[v]==0)
            {
                dep[v]=dep[u]+1;
                q.push(v);
            }
        }
    }
    if(dep[t])return 1;
    return 0;
}
int dfs(int u,int flow)
{
    if(u==t||flow==0)return flow;//到达汇点或者是没有流量，就返回流量
    int res=0;
    for(int &i=cur[u];i!=-1;i=e[i].next)
    {
        int v=e[i].to;
        if(e[i].w>0&&dep[v]==dep[u]+1)
        {
            int di=dfs(v,min(flow,e[i].w));//min(flow,e[i].w)表示起点到v的最小流量
            if(!di)continue;
            e[i].w-=di;
            e[i^1].w+=di;//反向边加上di
            res+=di;//res相当于从v点流出了多少流量(当前的流出流量作为后面点的供给)
            flow-=di;//flow相当于还可以流入多少流量到v点(给当前点的供给)
            //多路增广，不直接返回一条弧的流量，而是把所有弧都跑完或者没有流量后再返回res
            if(flow==0)break;
        }
    }
    if(res==0)dep[u]=-2;//炸点，使没有流量(不能再向后流出)的点不会再被访问
    //不写这句话就会超时！
    return res;
}
int dinic()
{
    int ans=0;
    while(bfs())//先bfs进行“探路”并分层，分层后进行多次dfs
    {
        for(int i=1;i<=n;i++)//比这个memcpy(cur,head,sizeof(head)) 要快一点
            cur[i]=head[i];
        while(int d=dfs(s,inf))//while循环的意义：只要dfs不为0，就一直dfs，直到找不到增广路
            ans+=d;
    }
    return ans;
}
int main()
{
    ios::sync_with_stdio(false);
    cin>>T;
    while(T--)
    {
        cnt=0;
        memset(head,-1,sizeof(head));
        cin>>n>>m;
        int x,y;
        int mi=inf,mx=-inf;
        for(int i=1;i<=n;i++)
        {
            cin>>x>>y;
            if(x<mi)//找横坐标最小的点，是源点
            {
                mi=x;
                s=i;
            }
            if(x>mx)//找横坐标最大的点，是汇点
            {
                mx=x;
                t=i;
            }
        }
        int a,b,w;
        for(int i=1;i<=m;i++)
        {
            cin>>a>>b>>w;
            add_edge(a,b,w);
        }
        int ans=dinic();
        printf("%d\n",ans);
    }
    return 0;
}
/*
2
5 7
4 5
3 1
3 3
3 0
0 0
1 3 3
2 3 4
2 4 3
1 5 6
4 5 3
1 4 4
3 4 2

ans:9
*/

POJ 3281 Dining

我觉得这题的难点就是建图，以及把这个看起来像二分图匹配的问题转化为最大流问题（不看题解，真以为是二分图匹配）。

限制条件：每种食物和水都只能被一头牛用一次，求最多能喂饱多少头牛。

把一头牛拆成两头（你没看错，就是这种拆点的神奇操作），然后建图：食物->牛->牛->饮料，最后再加一个超级源点连上每种食物，加一个超级汇点连上每种饮料，图中的任意一条增广路就变成了：超级源点->食物->牛(左)->牛(右)->饮料->超级汇点。

建立网络流模型：
1.对每种食物建立从源点指向它的一条边，流量为1
2.在牛与它所喜爱的食物间建立一条边，流量为1
3.在牛与它所喜欢的饮料间建立一条边，流量为1
4.对每种饮料建立一条指向汇点的边，流量为1
5.在上面的基础上，将牛拆点，在拆开的点间建立一条流量为1的边
在以上条件下，从源点到汇点的最大流即为答案

为什么要这样建图？原因如下：

模型的分析：
条件1使得满足每种食物有且只有一个，条件4类似
条件2使得每头牛只能选择自己喜欢的食物，条件3类似
条件5使得每头牛最多只能选择一种饮料和食物

还注意一个小细节：对牛的编号、食物编号、饮料编号要进行处理，防止它们编号重合。设食物 f 种，饮料 d 种，牛 n 头，则设左边牛的编号为[1,n]不变，拆点得到的右边牛的编号在原有基础上 +n ，食物编号在原有基础上 +2n ，饮料编号在原有基础上 +2n+f 。源点 s 编号为0，汇点 t 编号为2n+f+d+1。

AC代码：

//#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
const int N=1e3+10,M=1e5+10,inf=1e9;
bool vis1[N],vis2[N];
int n,s,t,cnt,head[N],dep[N];
struct edge
{
    int to,w,next;
}e[M<<1];
void add(int x,int y,int z)
{
    e[cnt].to=y;
    e[cnt].w=z;
    e[cnt].next=head[x];
    head[x]=cnt++;
}
void add_edge(int x,int y,int z)//加正向边和初始的反向边
{
    add(x,y,z);
    add(y,x,0);
}
bool bfs()
{
    queue<int>q;
    memset(dep,0,sizeof(dep));
    q.push(s);
    dep[s]=1;
    while(!q.empty())
    {
        int u=q.front();q.pop();
        for(int i=head[u];i!=-1;i=e[i].next)
        {
            int v=e[i].to;
            if(e[i].w>0&&dep[v]==0)
            {
                dep[v]=dep[u]+1;
                q.push(v);
            }
        }
    }
    if(dep[t])return 1;
    return 0;
}
int dfs(int u,int flow)
{
    if(u==t)return flow;
    for(int i=head[u];i!=-1;i=e[i].next)
    {
        int v=e[i].to;
        if(e[i].w>0&&dep[v]==dep[u]+1)
        {
            int di=dfs(v,min(flow,e[i].w));
            if(di>0)
            {
                e[i].w-=di;
                e[i^1].w+=di;
                return di;
            }
        }
    }
    return 0;
}
int dinic()
{
    int ans=0;
    while(bfs())
    {
        while(int d=dfs(s,inf))
            ans+=d;
    }
    return ans;
}
int main()
{
    ios::sync_with_stdio(false);
    memset(head,-1,sizeof(head));
    int f,d,q1,q2,x,y;
    cin>>n>>f>>d;
    s=0,t=2*n+f+d+1;
    for(int i=1;i<=n;i++)
    {
        cin>>q1>>q2;
        int cow1=i;//左边牛的编号
        int cow2=i+n;//右边牛的编号(拆点)
        while(q1--)
        {
            cin>>x;//食物
            x+=2*n;
            if(!vis1[x])
            {
                add_edge(s,x,1);//源点与食物连边
                vis1[x]=1;
            }
            add_edge(x,cow1,1);//食物与牛连边
        }
        add_edge(cow1,cow2,1);//牛与牛自身连边
        while(q2--)
        {
            cin>>y;//饮料
            y+=2*n+f;
            add_edge(cow2,y,1);//牛与饮料连边
            if(!vis2[y])
            {
                vis2[y]=1;
                add_edge(y,t,1);//饮料与汇点连边
            }
        }
    }
    int ans=dinic();
    printf("%d\n",ans);
    return 0;
}

POJ 3436 ACM Computer Factory

题意：

有N台组装电脑的机器。电脑的组成部分共有P部分。
每台机器有P个输入输出规格。还有一个容量Q；
其中输入规格有三种情况：0,1,2
0：该部分不能存在
1：该部分必须保留
2：该部分可有可无
输出规格有2种情况：0,1
0：该部分不存在
1：该部分存在
要求的是生产电脑最大的台数，就是求网络中的最大流。

建图：

1. 要增加源点和汇点。输入没有1的连接源点，输出全部是1的连接汇点。
2. 考虑到每台机器都有容量，所以把一台机器分成两个点，中间建一条容量的边。
3. 如果一台机器的输出符合另一台机器的输入(只要不是0->1和1->0就符合)，则建一条容量无穷大的边。

最后考虑处理输出边数问题，只要考虑退回边和原边的关系，退回边的权值就是原边流过的流量值，那么遍历所有反向边(边的编号为奇数的)，考虑其是否>0，如果是，则说明这条边有流流过，那么对应将其记录下来一起输出即可。

这题wa了无数次，最后发现是输出的顺序错了，写成了原料到产出，答案必须是写产出到原料，我以为这个顺序没关系（If several solutions exist, output any of them. 题意应该是说答案的行的顺序可以互换，没说行的内部顺序可以写反）

AC代码：

#include 
#include 
#include 
#include 
#include 
using namespace std;
const int N=52,M=1e5+10,P=12,inf=2e9;
int s,t,p,n,w,num,cnt,head[N],dep[N];
int a[N][P],b[N][P];//两个下标是行号和列号
struct node
{
    int u,v,w;
};
vector<node>path;
struct edge
{
    int from,to,w,next;
}e[M<<1];
void add(int x,int y,int z)
{
    e[cnt].from=x;
    e[cnt].to=y;
    e[cnt].w=z;
    e[cnt].next=head[x];
    head[x]=cnt++;
}
void add_edge(int x,int y,int z)//加正向边和初始的反向边
{
    add(x,y,z);
    add(y,x,0);
}
bool bfs()
{
    queue<int>q;
    memset(dep,0,sizeof(dep));
    q.push(s);
    dep[s]=1;
    while(!q.empty())
    {
        int u=q.front();q.pop();
        for(int i=head[u];i!=-1;i=e[i].next)
        {
            int v=e[i].to;
            if(e[i].w>0&&dep[v]==0)
            {
                dep[v]=dep[u]+1;
                q.push(v);
            }
        }
    }
    if(dep[t])return 1;
    return 0;
}
int dfs(int u,int flow)
{
    if(u==t)return flow;
    for(int i=head[u];i!=-1;i=e[i].next)
    {
        int v=e[i].to;
        if(e[i].w>0&&dep[v]==dep[u]+1)
        {
            int di=dfs(v,min(flow,e[i].w));
            if(di>0)
            {
                e[i].w-=di;
                e[i^1].w+=di;
                return di;
            }
        }
    }
    return 0;
}
int dinic()
{
    int ans=0;
    while(bfs())
    {
        while(int d=dfs(s,inf))
            ans+=d;
    }
    return ans;
}
bool judge(int numa,int numb)//判断从某个机器的产出能否连到其他机器的原料
{
    for(int i=1;i<=p;i++)
    {
        int x=a[numa][i];
        int y=b[numb][i];
        if((x==0&&y==1)||(x==1&&y==0))return 0;
    }
    return 1;
}
int main()
{
    ios::sync_with_stdio(false);
    cin>>p>>n;
    memset(head,-1,sizeof(head));
    s=0,t=2*n+1;
    for(int i=1;i<=n;i++)
    {
        cin>>w;
        int sum1=0;//统计每个原料结点或者产出结点中1的个数
        int numa=i;//原料结点编号
        int numb=i+n;//产出结点编号
        for(int j=1;j<=p;j++)
        {
            cin>>a[i][j];
            if(a[i][j]==1)sum1++;
        }
        if(sum1==0)add_edge(s,numa,inf);//将源点与不存在1的原料结点连边
        add_edge(numa,numb,w);//将同一机器的原料结点和产出结点连边
        sum1=0;
        for(int j=1;j<=p;j++)
        {
            cin>>b[i][j];
            if(b[i][j]==1)sum1++;
        }
        if(sum1==p)add_edge(numb,t,inf);//将全是1的产出结点与汇点连边
    }
    for(int i=1;i<=n;i++)//原料结点行号
    {
        for(int j=1;j<=n;j++)//产出结点行号
        {
            if(i==j)continue;
            if(judge(i,j))
            {
                //printf("link edge j=%d i=%d\n",j,i);
                add_edge(j+n,i,inf);//将机器j的产出结点连到机器i的原料结点
            }
        }
    }
    int ans=dinic();
    printf("%d ",ans);
    for(int i=1;i<=cnt;i+=2)//遍历反向边
    {
        int from=e[i].from;
        int to=e[i].to;
        int w=e[i].w;
        if(w>0&&from>=1&&from<=n&&to>=n+1&&to<=2*n&&from!=to-n)
            path.push_back({to-n,from,w});
            //就这个地方我写成了path.push_back({from,to-n,w})，wa了无数次！
    }
    printf("%d\n",path.size());
    for(int i=0;i<path.size();i++)
        printf("%d %d %d\n",path[i].u,path[i].v,path[i].w);
    return 0;
}
/*
3 4
15  0 0 0  0 1 0
10  0 0 0  0 1 1
30  0 1 2  1 1 1
3   0 2 1  1 1 1

ans:
25 3
1 3 15（不能写成3 1 15）
2 3 7
2 4 3
*/

POJ 1087 A Plug for UNIX

题意：

1. 在一个会议室里有n个插座(可能重复)；

2. 每个插座只能插一个电器的插头（或者适配器）；

3. 有m个电器，每个电器有一个插头需要插在相应一种插座上；

4. 不是所有电器都能在会议室找到相应插座；

5. 有k种适配器，每种适配器有无限多数量；

6. 每种适配器(s1, s2)可以把s1类插座变为s2类插座；

7. 问最后最少有多少个电器无法使用。

建图：

1. 各个电器各自为一个节点，和源点（不存在，自己构造）相连，且源点到电器的容量为1。

2. 将室内已有的插座各自为一个节点，和汇点（不存在，自己构造）相连，且到汇点的容量为1。

3. 将电器到其应该插的插座类型的点做边，且容量为1。

4. 将适配器(a, b)从a点到b点做边，且边的容量为INF。

需要注意，在输入电器以及输入适配器的过程中，如果遇到室内没有的插座类型，则需要在图中添加新的节点。

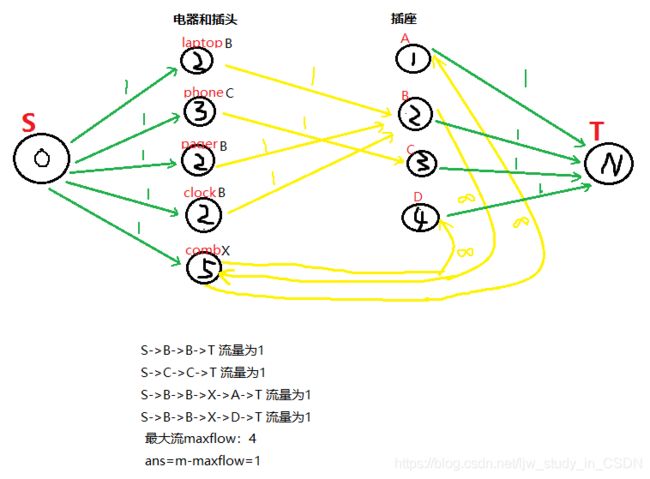
样例输入：

4
A
B
C
D
5
laptop B
phone C
pager B
clock B
comb X
3
B X
X A
X D

画图理解样例：

AC代码：

#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
const int N=1e4,M=1e5+10,inf=0x7f7f7f7f;
int n,m,k,s,t,cnt,head[N+10],dep[N+10];
map<string,int>vis;//存放电器的插头和提供的插座(包括适配器转换得到的插座)
struct edge
{
    int to,w,next;
}e[M<<1];
void add(int x,int y,int z)
{
    e[cnt].to=y;
    e[cnt].w=z;
    e[cnt].next=head[x];
    head[x]=cnt++;
}
void add_edge(int x,int y,int z)
{
    add(x,y,z);
    add(y,x,0);
}
bool bfs()
{
    queue<int>q;
    memset(dep,0,sizeof(dep));
    q.push(s);
    dep[s]=1;
    while(!q.empty())
    {
        int u=q.front();q.pop();
        for(int i=head[u];i!=-1;i=e[i].next)
        {
            int v=e[i].to;
            if(e[i].w>0&&dep[v]==0)
            {
                dep[v]=dep[u]+1;
                q.push(v);
            }
        }
    }
    if(dep[t])return 1;
    return 0;
}
int dfs(int u,int flow)
{
    if(u==t)return flow;//到达汇点，返回这条增广路上的最小流量
    for(int i=head[u];i!=-1;i=e[i].next)
    {
        int v=e[i].to;
        if(e[i].w>0&&dep[v]==dep[u]+1)
        {
            int di=dfs(v,min(flow,e[i].w));//min(flow,e[i].w)表示起点到v的最小流量
            if(di>0)//防止dfs结果return 0的情况，如果di=0会死循环
            {
                e[i].w-=di;
                e[i^1].w+=di;//反向边加上di
                return di;//di表示整条增广路上的最小流量，回溯的时候一直向上返回，返回的di是不变的
            }
        }
    }
    return 0;//找不到增广路，到不了汇点
}
int dinic()
{
    int ans=0;
    while(bfs())//先bfs进行“探路”并分层，分层后进行多次dfs
    {
        //每dfs一次，就尝试找到一条增广路并返回路上的最小流量
        while(int d=dfs(s,inf))//while循环的意义：只要dfs不为0，就一直dfs，直到找不到增广路
            ans+=d;
    }
    return ans;
}
int main()
{
    ios::sync_with_stdio(false);
    string s1,s2;
    memset(head,-1,sizeof(head));
    s=0,t=N;//源点s，汇点t(汇点编号大于所有点的个数就行)
    cin>>n;
    int num=0;
    for(int i=1;i<=n;i++)//遍历插座(可能有重复名字)
    {
        cin>>s1;//已提供的插座名字s1
        if(!vis[s1])vis[s1]=++num;
        //合并相同名字的插座，只留插座第一次出现的名字，其对应的编号为vis[s1]
        add_edge(vis[s1],t,1);//插座与汇点连边，容量为1
    }
    cin>>m;
    for(int i=1;i<=m;i++)//遍历插头(可能有重复)
    {
        cin>>s1>>s2;//电器名s1，电器对应的插头名s2
        if(!vis[s2])vis[s2]=++num;
        add_edge(s,vis[s2],1);//源点与插头连边，容量为1
    }
    cin>>k;
    for(int i=1;i<=k;i++)
    {
        cin>>s1>>s2;//插座s1可以转换到插座s2
        if(!vis[s1])vis[s1]=++num;//已经存在的名字中找不到s1，则将s1插入
        if(!vis[s2])vis[s2]=++num;
        //printf("link edge %d %d\n",vis[s1],vis[s2]);
        add_edge(vis[s1],vis[s2],inf);//将可以转换的两个插座相连，容量为无限
    }
    int maxflow=dinic();
    printf("%d\n",m-maxflow);
    return 0;
}
/*
16
A
D
X
A
D
A
D
X
D
A
D
D
X
D
X
D
14
CLOCK B
CLOCK B
CLOCK B
LAPTOP B
LAPTOP B
LAPTOP B
LAPTOP B
LAPTOP B
LAPTOP B
PAGER B
PAGER B
COMB X
CELL C
CELL C
4
C D
X D
B X
B A

ans:0
*/

UPD 2020.4.12

LOJ 127 / 洛谷 P4722【模板】最大流 加强版 / 预流推进

解决最大流问题有很多算法，诸如EK,Dinic,ISAP,HLPP等等。
今天看到了一篇很好的文章，比对了各个算法的适用场景和复杂度，可以看一下这篇博客：P4722 -【模板】最大流 加强版 / 预流推进

一般来说，Dinic算法是够用的，但是这个加强版的题数据很毒瘤，得用HLPP。

我先挖个坑，看什么时候HLPP算法给填了

看到一个用Dinic优化了一下卡过去的，(不是我写的)代码：

//C++ 17
#include
using namespace std;
const int maxn=1210,maxm=120010;
struct edge
{
    int u,v,cap;
}e[maxm];
struct Dinic
{
    int tp,s,t,dis[maxn],cur[maxn],que[maxn];
    vector<edge>e;vector<int>v[maxn];
    void AddEdge(int x,int y,int flw)
    {
        e.push_back(edge{x,y,flw});
        e.push_back(edge{y,x,0});
        v[x].push_back(e.size()-2);
    }
    int bfs()
    {
        memset(dis,0x3f,sizeof(dis));
        int l=1,r=1;que[1]=s;dis[s]=0;
        while(l<=r)
        {
            int p=que[l++],to;
            for(int i:v[p])if(e[i].cap&&dis[to=e[i].v]>1e9)
                dis[to]=dis[p]+1,que[++r]=to;
        }
        return dis[t]<1e9;
    }
    int dfs(int p,int a)
    {
        if(p==t||!a)return a;
        int sf=0,flw;
        for(int &i=cur[p],to;i<(int)v[p].size();++i)
        {
            edge &E=e[v[p][i]];
            if(dis[to=E.v]==dis[p]+1&&(flw=dfs(to,min(a,E.cap))))
            {
                E.cap-=flw;e[v[p][i]^1].cap+=flw;
                a-=flw;sf+=flw;
                if(!a)break;
            }
        }
        return sf;
    }
    int dinic(int s,int t,int tp=1)
    {
        this->s=s;this->t=t;this->tp=tp;
        int flw=0;
        while(bfs())
        {
            memset(cur,0,sizeof(cur));
            flw+=dfs(s,INT_MAX);
        }
        return flw;
    }
}sol;
int n,m,i,s,t,ans;
int main(){
    scanf("%d%d%d%d",&n,&m,&s,&t);
    for(i=0;i<m;i++)scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].cap);
    sort(e,e+m,[](edge a,edge b){return a.cap>b.cap;});
    for(int tp:{0,1})
        for(int p=1<<30,i=0;p;p/=2)
        {
            while(i<m&&e[i].cap>=p)
            {
                if(tp)sol.v[e[i].v].push_back(i*2+1);
                else sol.AddEdge(e[i].u,e[i].v,e[i].cap);
                i++;
            }
            ans+=sol.dinic(s,t,tp);
        }
    printf("%d\n",ans);
    return 0;
}