ACM_线段树
开始线段树的学习
几个概念
RMQ (Range Minimum/Maximum Query)问题是指:对于长度为n的数列A,回答若干询问RMQ(A,i,j)(i,j<=n),返回数列A中下标在i,j里的最小(大)值,也就是说,RMQ问题是指求区间最值的问题。
一.基础知识
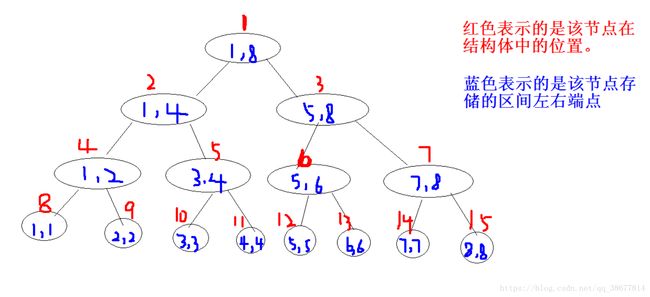
1、线段树是一棵二叉搜索树,它储存的是一个区间的信息。
2、每个节点以结构体的方式存储,结构体包含以下几个信息:
区间左端点、右端点;(这两者必有)
这个区间要维护的信息(事实际情况而定,数目不等)。
3、线段树的基本思想:二分。
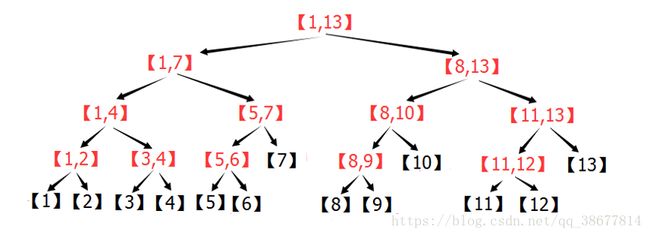
4、线段树一般结构如图所示:
5、特殊性质:
由上图可得,
1、每个节点的左孩子区间范围为[l,mid],右孩子为[mid+1,r]
2、对于结点k,左孩子结点为2*k,右孩子为2*k+1,这符合完全二叉树的性质
二.基本操作
基本有五个:建树、单点查询、单点修改、区间查询、区间修改。
数据结构如下
struct node
{
int l,r,w;//l,r分别表示区间左右端点,w表示区间和
}tree[4*n+1];1.建立线段树
void build(int l,int r,int k)
{
tree[k].l=l;tree[k].r=r;//表示下标
if(l==r)//叶子节点
{
scanf("%d",&tree[k].w);//如果是叶子节点把值存进来
return ; //别漏
}
int m=(l+r)/2;// 推荐写l+(r-l)/2 不过一般也无所谓
build(l,m,k*2);//左孩子 递归的妙用 k<<1 小优化
build(m+1,r,k*2+1);//右孩子 k<<1|1 小优化
tree[k].w=tree[k*2].w+tree[k*2+1].w;//状态合并,此结点的w=两个孩子的w之和
}2.单点查询
void ask(int k)
{
if(tree[k].l==tree[k].r) //当前结点的左右端点相等,是叶子节点,是最终答案
{
ans=tree[k].w;
return ;
}
int m=(tree[k].l+tree[k].r)/2;
if(x<=m) ask(k*2);//目标位置比中点靠左,就递归左孩子
else ask(k*2+1);//反之,递归右孩子
}ask(1) l=1 r=13
m=7
x=5<=m=7
ask(2) l=1 r=7
x=5>4
ask(5) l=5 r=7
x=5<m=6
ask(10) l=5 r=6
x=5<=m=5
ask(20)3.单点修改,即更改某一个点的状态。用引例中的例子,对第x个数加上y
牵一发而动全身
一个字:递归牛逼
void add(int k)
{
if(tree[k].l==tree[k].r)//找到目标位置
{
tree[k].w+=y;
return;
}
int m=(tree[k].l+tree[k].r)/2;
if(x<=m) add(k*2);
else add(k*2+1);
tree[k].w=tree[k*2].w+tree[k*2+1].w;//所有包含结点k的结点状态更新
}复杂度O(log2(n))
4、区间查询,即查询一段区间的状态,比如查询区间[x,y]的和
老套路递归
区间的话
三种情况
①刚好
②包含
③只有一段
void sum(int k)
{
if(tree[k].l>=x&&tree[k].r<=y) //包含在里面加上整段
{
ans+=tree[k].w;
return;
}
int m=(tree[k].l+tree[k].r)/2;
if(x<=m) sum(k*2);//递归找段 直至跳出递归
if(y>m) sum(k*2+1);
}
5.区间修改,即修改一段连续区间的值,我们已给区间[a,b]的每个数都加x为例讲解
可以想到,单点修改是区间修改的一种情况,那么我们对每个点单点修改使用技能“牵一发而动全身” 可你还要线段树干啥啊 这不更复杂了吗
盗用别人的图↓
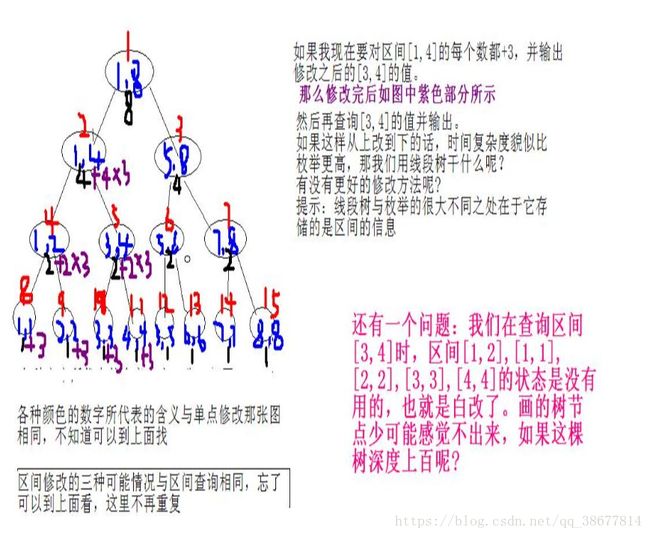
有人提出:修改的时候只修改对查询有用的点。
引入一个标记,称之为lazytag 懒标记!
懒,顾名思义,叫你干活你去干活,不叫你干活你就躺着
存储到这个节点的修改信息,暂时不把修改信息传到子节点
实现思路:
a.原结构体中增加新的变量,存储这个懒标记。
b.递归到这个节点时,只更新这个节点的状态,并把当前的更改值累积到标记中。注意是累积,可以这样理解:过年,很多个亲戚都给你压岁钱,但你暂时不用,所以都被你父母扣下了。
c.什么时候才用到这个懒标记?当需要递归这个节点的子节点时,标记下传给子节点。这里不必管用哪个子节点,两个都传下去。就像你如果还有妹妹,父母给你们零花钱时总不能偏心吧
d.下传操作:
3部分:①当前节点的懒标记累积到子节点的懒标记中。
②修改子节点状态。在引例中,就是原状态+子节点区间点的个数*父节点传下来的懒标记。
③父节点懒标记清0。这个懒标记已经传下去了,不清0后面再用这个懒标记时会重复下传。就像你父母给了你5元钱,你不能说因为前几次给了你10元钱, 所以这次得给你15元,那父母不就亏大了。
void down(int k)
{
tree[k*2].f+=tree[k].f;//父节点懒标记分别传递给左右儿子
tree[k*2+1].f+=tree[k].f;
tree[k*2].w+=tree[k].f*(tree[k*2].r-tree[k*2].l+1);//更新状态
tree[k*2+1].w+=tree[k].f*(tree[k*2+1].r-tree[k*2+1].l+1);//同上
tree[k].f=0;//清零父节点懒标记
}得到区间修改的代码
void add_interval(int k)
{
if(tree[k].l>=a&&tree[k].r<=b)//当前区间全部对要修改的区间有用
{
tree[k].w+=(tree[k].r-tree[k].l+1)*x;//(r-l)+1区间点的总数
tree[k].f+=x;
return;
}
if(tree[k].f) down(k);//懒标记下传。只有不满足上面的if条件才执行,所以一定会用到当前节点的子节点
int m=(tree[k].l+tree[k].r)/2;
if(a<=m) add(k*2);
if(b>m) add(k*2+1);
tree[k].w=tree[k*2].w+tree[k*2+1].w;//更改区间状态
}所以在使用了懒标记的程序中,单点查询、区间查询也要像区间修改那样,对用得到的懒标记下传。其实就是加上一句if(tree[k].f) down(k);,其余不变。
题目描述
如题,已知一个数列,你需要进行下面三种操作:
1.将某区间每一个数乘上x
2.将某区间每一个数加上x
3.求出某区间每一个数的和
输入输出格式
输入格式:
第一行包含三个整数N、M、P,分别表示该数列数字的个数、操作的总个数和模数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数,表示一个操作,具体如下:
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数乘上k
操作2: 格式:2 x y k 含义:将区间[x,y]内每个数加上k
操作3: 格式:3 x y 含义:输出区间[x,y]内每个数的和对P取模所得的结果
输出格式:
输出包含若干行整数,即为所有操作3的结果。
输入输出样例
输入样例#1: 复制
5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4
输出样例#1: 复制
17
2
#include 线段树的代码还真是冗长呢