Here We Go(relians) Again(HDU-2722)
Problem Description
The Gorelians are a warlike race that travel the universe conquering new worlds as a form of recreation. Given their violent, fun-loving nature, keeping their leaders alive is of serious concern. Part of the Gorelian security plan involves changing the traffic patterns of their cities on a daily basis, and routing all Gorelian Government Officials to the Government Building by the fastest possible route.
Fortunately for the Gorelian Minister of Traffic (that would be you), all Gorelian cities are laid out as a rectangular grid of blocks, where each block is a square measuring 2520 rels per side (a rel is the Gorelian Official Unit of Distance). The speed limit between two adjacent intersections is always constant, and may range from 1 to 9 rels per blip (a blip, of course, being the Gorelian Official Unit of Time). Since Gorelians have outlawed decimal numbers as unholy (hey, if you're the dominant force in the known universe, you can outlaw whatever you want), speed limits are always integer values. This explains why Gorelian blocks are precisely 2520 rels in length: 2520 is the least common multiple of the integers 1 through 9. Thus, the time required to travel between two adjacent intersections is always an integer number of blips.
In all Gorelian cities, Government Housing is always at the northwest corner of the city, while the Government Building is always at the southeast corner. Streets between intersections might be one-way or two-way, or possibly even closed for repair (all this tinkering with traffic patterns causes a lot of accidents). Your job, given the details of speed limits, street directions, and street closures for a Gorelian city, is to determine the fastest route from Government Housing to the Government Building. (It is possible, due to street directions and closures, that no route exists, in which case a Gorelian Official Temporary Holiday is declared, and the Gorelian Officials take the day off.)
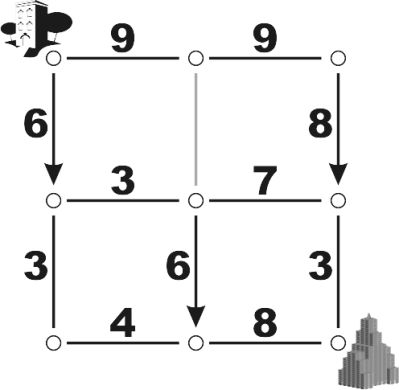
The picture above shows a Gorelian City marked with speed limits, one way streets, and one closed street. It is assumed that streets are always traveled at the exact posted speed limit, and that turning a corner takes zero time. Under these conditions, you should be able to determine that the fastest route from Government Housing to the Government Building in this city is 1715 blips. And if the next day, the only change is that the closed road is opened to two way traffic at 9 rels per blip, the fastest route becomes 1295 blips. On the other hand, suppose the three one-way streets are switched from southbound to northbound (with the closed road remaining closed). In that case, no route would be possible and the day would be declared a holiday.
Input
The input consists of a set of cities for which you must find a fastest route if one exists. The first line of an input case contains two integers, which are the vertical and horizontal number of city blocks, respectively. The smallest city is a single block, or 1 by 1, and the largest city is 20 by 20 blocks. The remainder of the input specifies speed limits and traffic directions for streets between intersections, one row of street segments at a time. The first line of the input (after the dimensions line) contains the data for the northernmost east-west street segments. The next line contains the data for the northernmost row of north-south street segments. Then the next row of east-west streets, then north-south streets, and so on, until the southernmost row of east-west streets. Speed limits and directions of travel are specified in order from west to east, and each consists of an integer from 0 to 9 indicating speed limit, and a symbol indicating which direction traffic may flow. A zero speed limit means the road is closed. All digits and symbols are delimited by a single space. For east-west streets, the symbol will be an asterisk '*' which indicates travel is allowed in both directions, a less-than symbol '<' which indicates travel is allowed only in an east-to-west direction, or a greater-than symbol '>' which indicates travel is allowed only in a west-to-east direction. For north-south streets, an asterisk again indicates travel is allowed in either direction, a lowercase "vee" character 'v' indicates travel is allowed only in a north-to-south directions, and a caret symbol '^' indicates travel is allowed only in a south-to-north direction. A zero speed, indicating a closed road, is always followed by an asterisk. Input cities continue in this manner until a value of zero is specified for both the vertical and horizontal dimensions.
Output
For each input scenario, output a line specifying the integer number of blips of the shortest route, a space, and then the word "blips". For scenarios which have no route, output a line with the word "Holiday".
Sample Input
2 2
9 * 9 *
6 v 0 * 8 v
3 * 7 *
3 * 6 v 3 *
4 * 8 *
2 2
9 * 9 *
6 v 9 * 8 v
3 * 7 *
3 * 6 v 3 *
4 * 8 *
2 2
9 * 9 *
6 ^ 0 * 8 ^
3 * 7 *
3 * 6 ^ 3 *
4 * 8 *
0 0Sample Output
1715 blips
1295 blips
Holiday
题意:已知n*m大小的矩形,起点在左上, 终点在右下,里面每一个矩形代表一个区。每个区的边长是2520,每个区的边有一速度限制,范围是0~9, 如果是0则说明边不能行驶,求从起点到终点的最短路。
思路:题不难,三种算法均可实现,难点在于输入部分,由上到下,由左到右,按照上图所示的对应位置输入数据,每一条边是 数字+空格+符号的形式, 数字表示限速, 符号表示路是单向是双向,路还分东西南北。
Source Program
#include
#include
#include
#include
#include
#include
#include
#include
#define INF 0x3f3f3f3f//图论中无穷大的设定,如果取0x7fffffff,那么路径会溢出而变成负数,而0x3f3f3f3f的十进制是1061109567,与0x7fffffff都是10^9的数量级,而且小于0x7fffffff,所以它可作为无穷大使用而不致出现数据大于无穷大的情形
#define N 501
#define MOD 2520
#define E 1e-12
using namespace std;
int v,h;
int g[N][N],dis[N];
bool vis[N];
int main ()
{
while(scanf("%d%d",&v,&h)!=EOF&&(v||h))
{
int ver=1,hor=1;
memset(g,INF,sizeof(g));
/*输入处理*/
for(int i=1;i<=2*v+1;i++)
{
for(int j=1;j<=h+(!(i%2));j++)
{
int x,y;
int dis,dis1,dis2;
char ch;
scanf("%d %c",&dis,&ch);
if(dis==0)//d为0,路不通
ch=0;
if(i%2)//横向
{
x=j+(h+1)*(hor-1);
y=x+1;
if(ch=='*' || ch=='>')
dis1=MOD/dis;
else
dis1=INF;
if(ch=='*' || ch=='<')
dis2=MOD/dis;
else
dis2=INF;
}
else//纵向
{
x=j+(h+1)*(ver-1);
y=j+(h+1)*ver;
if(ch=='*' || ch=='v')
dis1=MOD/dis;
else
dis1=INF;
if(ch=='*' || ch=='^')
dis2=MOD/dis;
else
dis2=INF;
}
g[x][y]=dis1;
g[y][x]=dis2;
}
if(i%2)//横向遇到单数+1
hor++;
else//纵向时遇到双数+1
ver++;
getchar();
}
/*Dijkstra算法寻找最短路*/
int x=1,y=(v+1)*(h+1);
memset(vis,0,sizeof(vis));
for(int i=1;i<=y;i++)
dis[i]=g[x][i];
dis[x]=0;
for(int i=1;i<=y;i++)
{
int k=0;
int minn=INF;
for(int j=1;j<=y;j++)
{
if(!vis[j]&&dis[j]