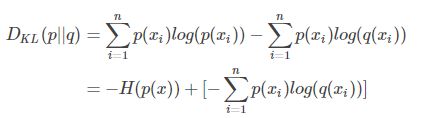DL中loss之交叉熵
文章目录
- 1.原理剖析
- 1.1.信息量
- 2.1.熵
- 1.3.相对熵(KL散度)
- 1.4.交叉熵
- 2.应用实例
- 2.1 交叉熵在单分类中使用
- 2.2.交叉熵在多分类问题中的使用
最近整理常见的loss函数,为了理解深刻,在对比之前先了解各种loss函数的原理
在介绍交叉熵之前,先一步一步来进行剖析
1.原理剖析
1.1.信息量
首先是信息量。假设我们听到了两件事,分别如下:
事件A:巴西队进入了2018世界杯决赛圈。
事件B:中国队进入了2018世界杯决赛圈。
仅凭直觉来说,显而易见事件B的信息量比事件A的信息量要大。究其原因,是因为事件A发生的概率很大,事件B发生的概率很小。所以当越不可能的事件发生了,我们获取到的信息量就越大。越可能发生的事件发生了,我们获取到的信息量就越小。那么信息量应该和事件发生的概率有关。
假设X是一个离散型随机变量,其取值集合为χχ,概率分布函数 p ( x ) = P r ( X = x ) , x ∈ χ p(x)=Pr(X=x),x∈χ p(x)=Pr(X=x),x∈χ,则定义事件X=x0X=x0的信息量为:
I ( x 0 ) = − l o g ( p ( x 0 ) ) I(x_0)=−log(p(x_0)) I(x0)=−log(p(x0))
由于是概率所以 p ( x 0 ) p(x_0) p(x0)的取值范围是[0,1],绘制为图形如下:

2.1.熵
考虑另一个问题,对于某个事件,有n种可能性,每一种可能性都有一个概率p(xi)
这样就可以计算出某一种可能性的信息量。举一个例子,假设你拿出了你的电脑,按下开关,会有三种可能性,下表列出了每一种可能的概率及其对应的信息量
| 序号 | 事件 | 概率p | 信息量I |
|---|---|---|---|
| A | 电脑正常开机 | 0.7 | -log(p(A))=0.36 |
| B | 电脑无法开机 | 0.2 | -log(p(B))=1.61 |
| C | 电脑爆炸了 | 0.1 | -log(p(C ))=2.30 |
我们现在有了信息量的定义,而熵用来表示所有信息量的期望,即:
H ( X ) = − ∑ i = 1 n p ( x i ) l o g ( p ( x i ) ) H(X)=-\sum_{i=1}^n p(x_i)log(p(x_i)) H(X)=−i=1∑np(xi)log(p(xi))
然而有一类比较特殊的问题,比如投掷硬币只有两种可能,字朝上或花朝上。买彩票只有两种可能,中奖或不中奖。我们称之为0-1分布问题(二项分布的特例),对于这类问题,熵的计算方法可以简化为如下算式:

1.3.相对熵(KL散度)
相对熵又称KL散度,如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x),我们可以使用 KL 散度(Kullback-Leibler (KL) divergence)来衡量这两个分布的差异
在机器学习中,P往往用来表示样本的真实分布,比如[1,0,0]表示当前样本属于第一类。Q用来表示模型所预测的分布,比如[0.7,0.2,0.1]
直观的理解就是如果用P来描述样本,那么就非常完美。而用Q来描述样本,虽然可以大致描述,但是不是那么的完美,信息量不足,需要额外的一些“信息增量”才能达到和P一样完美的描述。如果我们的Q通过反复训练,也能完美的描述样本,那么就不再需要额外的“信息增量”,Q等价于P。
KL散度的计算公式:
(1.3) D K L ( p ∣ ∣ q ) = ∑ i = 1 n p ( x i ) l o g ( p ( x i ) q ( x i ) ) D_{KL}(p||q)=\sum_{i=1}^np(x_i)log(\frac{p(x_i)}{q(x_i)}) \tag {1.3} DKL(p∣∣q)=i=1∑np(xi)log(q(xi)p(xi))(1.3)
n为事件的所有可能性。
D K L D_{KL} DKL的值越小,表示q分布和p分布越接近
1.4.交叉熵
等式的前一部分恰巧就是p的熵,等式的后一部分,就是交叉熵:
H ( p , q ) = − ∑ i = 1 n p ( x i ) l o g ( q ( x i ) ) H(p,q)=-\sum_{i=1}^np(x_i)log(q(x_i)) H(p,q)=−i=1∑np(xi)log(q(xi))
在机器学习中,我们需要评估label和predicts之间的差距,使用KL散度刚刚好,即D_{KL}(y||\hat{y}),由于KL散度中的前一部分-H(y)不变,故在优化过程中,只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss,评估模型。
2.应用实例
2.1 交叉熵在单分类中使用
这里的单类别是指,每一张图像样本只能有一个类别,比如只能是狗或只能是猫。
交叉熵在单分类问题上基本是标配的方法
l o s s = − ∑ i = 1 n y i l o g ( y i ^ ) loss=-\sum_{i=1}^{n}y_ilog(\hat{y_i}) loss=−i=1∑nyilog(yi^)
上式为一张样本的loss计算方法。式2.1中n代表着n种类别。
对应的标签和预测值:
| - | 猫 | 青蛙 | 老鼠 |
|---|---|---|---|
| Label | 0 | 1 | 0 |
| Pred | 0.3 | 0.6 | 0.1 |
对应一个batch的loss就是:
l o s s = − 1 m ∑ j = 1 m ∑ i = 1 n y j i l o g ( y j i ^ ) loss=-\frac{1}{m}\sum_{j=1}^m\sum_{i=1}^{n}y_{ji}log(\hat{y_{ji}}) loss=−m1j=1∑mi=1∑nyjilog(yji^)
m为当前batch的样本数
2.2.交叉熵在多分类问题中的使用
这里的多类别是指,每一张图像样本可以有多个类别,比如同时包含一只猫和一只狗
和单分类问题的标签不同,多分类的标签是n-hot。
比如下面这张样本图,即有青蛙,又有老鼠,所以是一个多分类问题
对应的标签和预测值
| * | 猫 | 青蛙 | 老鼠 |
|---|---|---|---|
| Label | 0 | 1 | 1 |
| Pred | 0.1 | 0.7 | 0.8 |
值得注意的是,这里的Pred不再是通过softmax计算的了,这里采用的是sigmoid。将每一个节点的输出归一化到[0,1]之间。所有Pred值的和也不再为1。换句话说,就是每一个Label都是独立分布的,相互之间没有影响。所以交叉熵在这里是单独对每一个节点进行计算,每一个节点只有两种可能值,所以是一个二项分布。前面说过对于二项分布这种特殊的分布,熵的计算可以进行简化。
同样的,交叉熵的计算也可以简化,即:
l o s s = − y l o g ( y ^ ) − ( 1 − y ) l o g ( 1 − y ^ ) loss =-ylog(\hat{y})-(1-y)log(1-\hat{y}) loss=−ylog(y^)−(1−y)log(1−y^)
注意,上式只是针对一个节点的计算公式。这一点一定要和单分类loss区分开来。
例子中可以计算为:
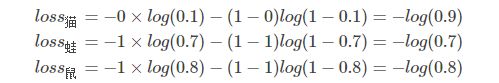
单张样本的loss即为 l o s s = l o s s 猫 + l o s s 蛙 + l o s s 鼠 loss=loss{猫}+loss{蛙}+loss_{鼠} loss=loss猫+loss蛙+loss鼠
每一个batch的loss就是:
l o s s = ∑ j = 1 m ∑ i = 1 n − y j i l o g ( y j i ^ ) − ( 1 − y j i ) l o g ( 1 − y j i ^ ) loss =\sum_{j=1}^{m}\sum_{i=1}^{n}-y_{ji}log(\hat{y_{ji}})-(1-y_{ji})log(1-\hat{y_{ji}}) loss=j=1∑mi=1∑n−yjilog(yji^)−(1−yji)log(1−yji^)
式中m为当前batch中的样本量,n为类别数。
参考链接:
一文搞懂交叉熵在机器学习中的使用,透彻理解交叉熵背后的直觉