数字正交下变频（多相滤波法）

[TOC]

---

多相滤波原理

在上一篇文章中讨论了基于低通滤波方式的正交下变频系统。下面是该种方式的结构图。

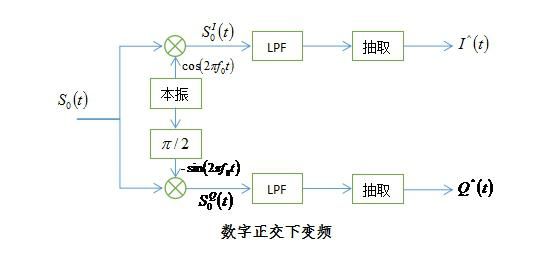
图1.1 数字正交下变频

但是，这种典型的数字下变频方式也存在着这样一些缺陷：
* 当采样信号为宽带信号时，需要较高的采样频率，此时会带来系统设计的复杂度；
* 先滤波后抽取，那些没被抽取的数据相当于是冗余数据，浪费了一定的运算量。
针对这些缺陷，可用多相滤波的方式进行改善。下面我们进行介绍。
多相滤波，本质上是采用抽取的方式，利用多个低阶FIR滤波器来代替一个高阶FIR滤波器，从而达到降低运算量的效果。
下面对其进行理论推导：

H(z)=∑n=−∞+∞h(n)z−n=∑k=0M−1z−k∑n=−∞+∞h(nM+k)(zM)−n

令

Ek(z)=∑n=−∞+∞h(nM+k)z−n

则

H(z)=∑k=0M−1z−kEk(zM)

其结构图如下:

图1.2 多相滤波结构

该结构与下面结构等效：

图1.2 多相滤波结构

下面举个简单的例子进行说明。
假设滤波器传递函数

H(z)=1+2z−1+3z−2+4z−3

我们假设抽取的间隔 M=2 ,那么滤波器传递函数可以写成

H(z)=(1+3z−2)+z−1(2+4z−2)

其中 1+3z−2 和 2+4z−2 分别为两个分支上的FIR滤波器的系统函数，且 z−2 表示该分支滤波器的输入数据应在原来滤波器的输入数据上进行 M=2 的抽取。第二个分支FIR滤波器传递函数前的 z−1 表示每个分支滤波器都需要经过一个延迟节。
直观上来理解，就是回波数据在多相滤波的过程中，对数据进行抽取，抽取得到的 M 路数据如下表所示。

分支号	抽取数据索引
1	1,M+1,2M+1,......
2	2,M+2,2M+2,......
3	3,M+3,2M+3,......
……	……

同样，滤波器系数也要经过相应的抽取，抽取的数据下标也和上表一致。
经过抽取后数据和滤波器系数进行卷积，最后将所有支路结果求和即可得到滤波结果。

---

多相滤波仿真

同样以雷达系统中的接收机系统为例，进行仿真。多相滤波方式的正交下变频方式处理顺序为： 混频 ——> 抽取 ——> 滤波，下面为具体参数设置。

参数	名称	取值	备注
f0	中频	20MHz
B	带宽	2MHz
tau	时宽	150us
T	重复周期	2ms
fs	采样频率	33MHz
SNR	信噪比	20dB
dis	目标距离	T∗fs/2	将目标设置在回波中间
M	抽样间隔	3

关于上面表格中的采样频率设置，下面表格根据带通采样定理给出一些可能情况。

n 取值	取值
2	(21,38)
3	(14,19)
4	(10.5,12.6)
5	(8.4,9.5)
6	(7,7.6)
……	……

采样频率可取上面表格中区间内的任何值，为使硬件处理方便，通常选取与中频存在倍数关系的取值。
**在这里存在一个疑问，假设采样频率为 fS ，抽取的间隔为 M ，那么每条支路上数据的采样频率就应该为 fs/M ,而此时信号中频仍为 f0 ，每条支路都必须满足带通采样定理，那么就应该用 fs/M 和 f0 来判断采样频率的选取是否合适。
而从另一个角度理解，多相滤波不过是常规低通滤波方式的数学上的优化，低通滤波方式是以采样频率 fS 和中频 f0 来判断频率的选取是否合适的，此处为什么会有矛盾。是不是因为抽取的先后顺序导致的呢？**
下面是仿真的结果。
下图是带中频的线性调频信号。

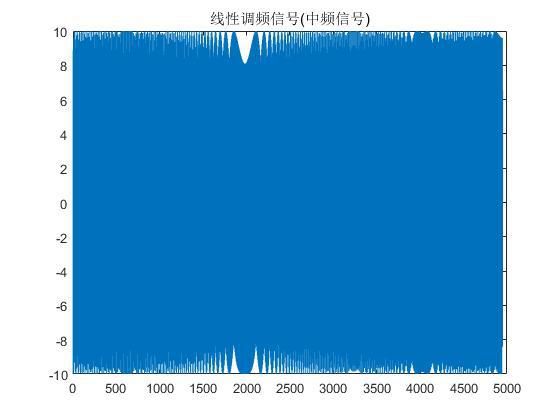
图2.1 带中频线性调频信号

在线性调频信号的基础上，添加高斯白噪声，回波信号及其频谱如下所示。

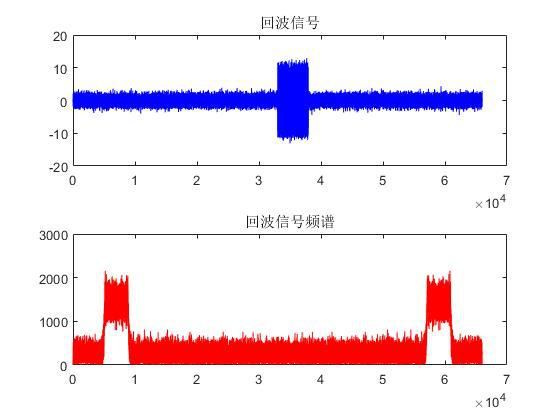
图2.2 带高斯白噪声回波信号

利用两路本振信号对回波信号进行正交混频，下图为混频之后的时序部信号。

图2.3 混频后信号

下图为混频后信号的幅频特性，其中包括基带部分和两倍中频部分。

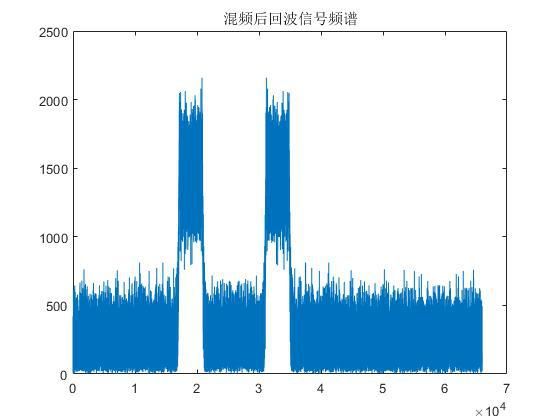
图2.4 混频后信号频谱


利用海明窗生成低通滤波器，并进行抽取。

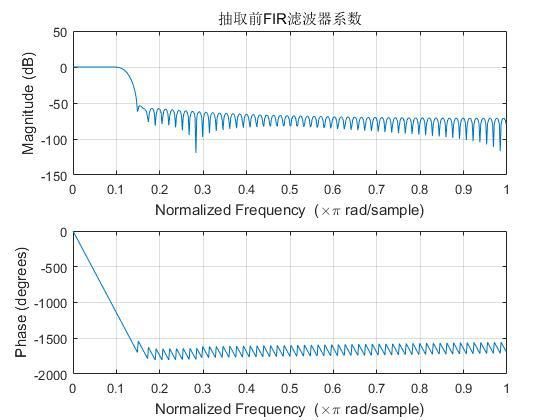
图2.5 滤波器系数

对回波信号进行抽取，下面为抽取后其中一条支路信号时域信号和频谱。



图2.6 某条支路抽取后信号及其幅频特性

对所有支路信号进行滤波累加，得到如下结果。

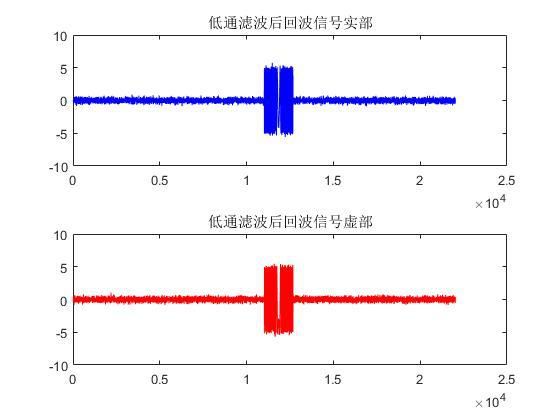
图2.7 滤波结果


上面的仿真采样频率采用的是33MHz，抽取后采样频率为11MHz，都满足带宽采样定理，所以DDC后看到的线性调频信号结果很好。如果采样频率更换成30MHz，此时是满足带通采样定理的，但是如果抽取后，变成10MHz，那么就会出现问题，DDC后结果如下所示，波形明显不正确。



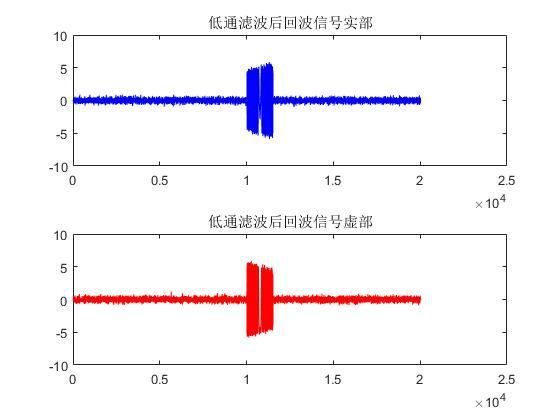
图2.8 更换采样频率后滤波结果


查看混频和抽取后的回波信号频谱，两倍的中频部分和基带信号频谱已经混叠了。

图2.9 更换采样频率后滤波后频谱

---

仿真代码附录

%% ddc
clear ; close all; clc;

% parameter
f0      =   20e+6;      % 中频 
B       =   2e+6;       % 带宽
Tao     =   150e-6;     % 时宽
T       =   2e-3;       % 脉冲重复周期 
fs      =   33e+6;      % 采样频率
SNR     =   20;         % 信噪比
dis     =   T*fs/2;     % 将目标设置在回波中间处
extract_num = 3;

% Generate LFM @f0
t = -round(Tao*fs/2):1:round(Tao*fs/2)-1; % 脉冲采样点 
median_fre = (10^(SNR/20))* (cos(pi*B/Tao*(t/fs).^2 ).*cos(2*pi*f0*t/fs) - sin(pi*B/Tao*(t/fs).^2 ).*sin(2*pi*f0*t/fs));   % I*cos + Q*sin

figure; plot(median_fre); title('线性调频信号(中频信号)');

% Generate echo
echo  = zeros(1,T*fs);
echo(dis:1:dis+Tao*fs-1) = median_fre;
noise = normrnd(0,1,1,T*fs);
% noise = 0.5*ones(1,T*fs);
echo = echo + noise;

figure;
subplot(2,1,1); plot(echo,'b'); title('回波信号');
subplot(2,1,2); plot(abs(fftshift(fft(echo))),'r'); title('回波信号频谱');

% frequence mixing
echo = echo.*exp(-1i*2*pi*f0*(0:1:T*fs-1)/fs);

figure;
subplot(2,1,1); plot(real(echo),'b'); title('混频后回波信号实部');
subplot(2,1,2); plot(imag(echo),'r'); title('混频后回波信号虚部');

figure; plot(abs(fftshift(fft(echo)))); title('混频后回波信号频谱');

% Multi-phase filtering 
% generate fir filter   order = 127 
coeff = fir1(127, B/(fs/2), hamming(128)); % w = B/(fs/2)
figure; freqz(coeff); title('抽取前FIR滤波器系数')

% extract by extract_num

for k = 1:1:extract_num
    coeff_extra(k,:) = coeff(k:extract_num:floor(length(coeff)/extract_num)*extract_num );
end

figure;freqz(coeff_extra(1,:)); title('抽取后FIR滤波器系数')

% downsample by extract_num

for k = 1:1:extract_num
    echo_extra(k,:) = echo(k:extract_num:floor(length(echo)/extract_num)*extract_num);
end

figure; 
subplot(2,1,1); plot(real(echo_extra(1,:).')); title('抽取后信号')
subplot(2,1,2); plot(abs(fftshift(fft(echo_extra(1,:).')))); title('抽取后信号频谱')

% result

for k = 1:1:extract_num
    res(k,:) = conv(echo_extra(k,:),coeff_extra(k,:));
end

ddc_res = sum(res); % plus by row

figure;
subplot(2,1,1); plot(real(ddc_res),'b'); title('低通滤波后回波信号实部');
subplot(2,1,2); plot(imag(ddc_res),'r'); title('低通滤波后回波信号虚部');

---

参考资料：
[1] 《现代雷达系统分析与设计》陈伯孝编著。