有点小意思

卡尔曼滤波系列——（四）无损卡尔曼滤波

1 简介

无损卡尔曼滤波又称无迹卡尔曼滤波（Unscented Kalman Filter，UKF），是无损变换（Unscented Transform，UT）与标准卡尔曼滤波体系的结合，通过UT变换使非线性系统方程适用于线性假设下的标准卡尔曼体系。

与EKF不同的是，UKF是通过无损变换使非线性系统方程适用于线性假设下的标准Kalman滤波体系，而不是像EKF那样，必须通过线性化非线性函数实现递推滤波。

UKF的基本思想是卡尔曼滤波与无损变换，它能有效地克服EKF估计精度低、稳定性差的问题，因为不用忽略高阶项，所以对于非线性分布统计量的计算精度高。

2 基本算法

2.1 非线性系统状态估计原理

离散系统的状态转移方程和观测方程为

${{\mathbf{\theta }}_{k}}=f({{\mathbf{\theta }}_{k-1}})+{{\mathbf{s}}_{k}}$

${{\mathbf{z}}_{k}}=h({{\mathbf{\theta }}_{k}})+{{\mathbf{v}}_{k}}$

不管条件密度函数 ${{p}_{\mathbf{\theta }|\mathbf{z}}}(\mathbf{\theta }|\mathbf{z})$ 的特性如何，最小均方误差估计就是条件均值 ${{\mu }_{\mathbf{\theta }|\mathbf{z}}}=E[\mathbf{\theta }|\mathbf{z}]$ ，其中 $E[\cdot ]$ 表示期望的计算。

非线性系统的状态估计分成一步预测和测量修正两个步骤：

（1）一步预测

$\mathbf{\theta }_{k}^{'}=E[{{\mathbf{\theta }}_{k}}|{{\mathbf{z}}^{k-1}}]$

根据所有过去时刻的观测信息对状态做最小均方误差做预测，其协方差矩阵为 $\mathbf{\Sigma }_{_{k}}^{'}$

$\mathbf{\Sigma }_{_{k}}^{'}=\left\langle \mathbf{e}_{k}^{'}\mathbf{e}{{_{k}^{'}}^{T}} \right\rangle =\left\langle \left( {{\theta }_{k}}-\theta _{k}^{'} \right){{\left( {{\theta }_{k}}-\theta _{k}^{'} \right)}^{T}} \right\rangle$

（2）观测修正

引入卡尔曼增益 ${{\mathbf{K}}_{k}}$ ，利用实际观测值 $\mathbf{z}_{k}$ 与预测的观测值 $\mathbf{z}_{k}^{'}$ 的差异，对预测值 $\mathbf{\theta }_{k}^{'}$ 进行修正

$\left\langle {{\mathbf{\theta }}_{k}} \right\rangle =E[{{\mathbf{\theta }}_{k}}|{{\mathbf{z}}^{k}}]=\mathbf{\theta }_{k}^{'}+{{\mathbf{K}}_{k}}({{\mathbf{z}}_{k}}-\mathbf{z}_{k}^{'})$

${{\mathbf{K}}_{k}}={{\mathbf{\Sigma }}_{\mathbf{\theta z}}}\left( k \right)\cdot \mathbf{\Sigma }_{\mathbf{z}}^{-1}\left( k \right)$

其中 $\mathbf{z}_{k}^{'}$ ， ${{\mathbf{\Sigma }}_{\mathbf{\theta z}}}\left( k \right)$ 和 $\mathbf{\Sigma }_{\mathbf{z}}^{-1}\left( k \right)$ 的计算公式分别为

$\mathbf{z}_{k}^{'}=E\left[ {{\mathbf{z}}_{k}}|{{\mathbf{Z}}^{k-1}} \right]$

${{\mathbf{\Sigma }}_{\mathbf{\theta z}}}\left( k \right)=E\left\{ \left. \left[ {{\mathbf{\theta }}_{k}}-\mathbf{\theta }_{k}^{'} \right]{{\left[ {{\mathbf{z}}_{k}}-h\left( \mathbf{\theta }_{k}^{'} \right) \right]}^{T}} \right|{{\mathbf{Z}}^{k-1}} \right\}$

${{\mathbf{\Sigma }}_{\mathbf{z}}}\left( k \right)=E\left\{ \left. \left[ {{\mathbf{z}}_{k}}-h\left( \mathbf{\theta }_{k}^{'} \right) \right]{{\left[ {{\mathbf{z}}_{k}}-h\left( \mathbf{\theta }_{k}^{'} \right) \right]}^{T}} \right|{{\mathbf{Z}}^{k-1}} \right\}$

其中 ${{\mathbf{z}}_{k}}$ 表示第次观测向量的值， ${{\mathbf{Z}}^{k-1}}$ 表示前次观测向量的值的集合。那么估计值与真实值的误差协方差矩阵为

${{\mathbf{\Sigma }}_{k}}=E\left\{ \left. \left[ {{\mathbf{\theta }}_{k}}-\left\langle {{\mathbf{\theta }}_{k}} \right\rangle \right]{{\left[ {{\mathbf{\theta }}_{k}}-\left\langle {{\mathbf{\theta }}_{k}} \right\rangle \right]}^{T}} \right|{{\mathbf{Z}}^{k}} \right\}=\mathbf{\Sigma }_{k}^{'}-{{\mathbf{K}}_{k}}{{\mathbf{\Sigma }}_{\mathbf{z}}}\left( k \right)\mathbf{K}_{k}^{T}$

一般来说，近似非线性函数的概率密度分布比近似非线性函数本身更加容易，因此便有了粒子滤波PF和无迹卡尔曼滤波UKF。粒子滤波通过使用参考分布，随机产生大量粒子，用粒子的分布近似为状态的后验概率密度函数，进而计算得到系统状态的估计，他的主要缺点为粒子数越大计算量就越大，而减少粒子数又会导致整体估计性能下降。而无迹卡尔曼滤波则利用UT变换的思想，使得非线性系统能够适用于线性假设下的卡尔曼滤波体系，其采样形式为确定性采样，在粒子数相对PF较少的情况下，获得较高的逼近精度。

2.2 UT变换

UT变换是用固定数量的参数去近似一个高斯分布，其实现原理为：在原先分布中按某一规则取一些点，使这些点的均值为协方差状态分布与原状态分布的均值和协方差相等；将这些点代入非线性函数中，相应得到非线性函数值点集，通过这些点集可求取变换的均值和协方差。UT变换的实现一般分为以下三个步骤：

（1）构造Sigma点集

根据随机变量 $\mathbf x$ 的统计量均值 $\bar{\mathbf x}$ 和协方差 $\mathbf {P}_{x}$ （如果是标量，则为方差），构造Sigma点集

其中 $\lambda$ 为尺度参数，调整其值可以提高逼近精度，为变量 $\mathbf x$ 的维度。用这一组采样点可以近似地表示变量 $\mathbf x$ 的高斯分布。

（2）对Sigma点集做非线性变换

${{\mathbf Y}_{i}}=f({{\mathbf \chi }_{i}}),i=0,1,...,2n$

经过变换后的Sigma点集 $\left\{ {{\mathbf Y}_{i}} \right\}$ 即可近似地表示 $\mathbf{y}=f(\mathbf{x})$ 的分布。

（3）计算函数映射后的均值和方差

对变换后的Sigma点集 $\left\{ {{\mathbf Y}_{i}} \right\}$ 做加权处理，从而得到输出量 $\mathbf y$ 的均值 $\bar{\mathbf y}$ 和方差 $\mathbf {P}_{y}$

$\mathbf{\bar{y}}\approx \sum\limits_{i=1}^{2n}{W_{i}^{(m)}}{{\mathbf{Y}}_{i}}$

${{\mathbf{\bar{P}}}_{y}}\approx \sum\limits_{i=1}^{2n}{W_{i}^{(c)}}({{\mathbf{Y}}_{i}}-\mathbf{\bar{y}}){{({{\mathbf{Y}}_{i}}-\mathbf{\bar{y}})}^{T}}$

权重 $W_{i}^{(m)}$ 和 $W_{i}^{(c)}$ 的计算如下：

$W_{0}^{(c)}=\frac{\lambda }{n+\lambda }+\left( 1-{{\alpha }^{2}}+\beta \right)$ ， $W_{0}^{(m)}=\frac{\lambda }{n+\lambda }$

$W_{i}^{(c)}=W_{i}^{(m)}=\frac{1}{2\left( n+\lambda \right)},i=1,2,...,2n$

其中参数 $\kappa$ 为第二个尺度参数，通常设置为或； $\alpha$ 的取值一般在 $[1e^{-4},1)$ 区间内； $\beta$ 为状态分布参数，对高斯分布的变量， $\beta =2$ 最优，如果状态变量是标量的话，则 $\beta =0$ 最优。

以上就是UT变化的三个步骤，其变换的示意图大致如下图所示：

算法的实现流程原理图如下图所示，图中参数 $a=\sqrt{n+\kappa }$ 与相当于本博文中的 $\sqrt{n+\lambda }$ ，希望读者不要误解：

UT变换具有以下特点：

对非线性函数的概率密度分布进行近似，而不是对非线性函数做近似，算法实现不受模型复杂度的影响；
所得到的的非线性函数的统计量的准确性可以达到三阶，而之前EKF的准确性只能达到一阶；
无需计算Jacobi矩阵，这样就能处理不可导的非线性函数。

那么如何把UT变化应用到卡尔曼滤波框架中呢？笔者将在下一节给出。

3 UKF滤波算法

UKF=UT+KF，算法的实现分成两步走：

（1）状态的时间更新

选定状态的个Sigma点；

利用UT变换计算后验均值和方差；

（2）状态的观测更新

利用标准的卡尔曼滤波体系更新，但使用的公式有所差异。

根据系统的噪声的存在方式，将其分为加性噪声和隐含噪声，对于两种噪声，UKF滤波的处理方式分为两种，分别是简化的UKF和扩维的UKF，这里仍然假设噪声是高斯分布的。

3.1 简化UKF滤波算法（加性噪声）

系统的状态转移方程和观测方程为

$\small {{\mathbf{\theta }}_{k}}=f({{\mathbf{\theta }}_{k-1}})+{{\mathbf{s}}_{k}}$ ， $\small {{\mathbf{s}}_{k}}\sim \mathcal{N}(0,\mathbf{Q})$

$\small {{\mathbf{z}}_{k}}=h({{\mathbf{\theta }}_{k}})+{{\mathbf{v}}_{k}}$ ， $\small {{\mathbf{v}}_{k}}\sim \mathcal{N}(0,\mathbf{R})$

简化UKF滤波算法的流程为：

（1）初始化

$\left\langle {{\mathbf{\theta }}_{0}} \right\rangle =E\left[ {{\mathbf{\theta }}_{0}} \right]$

${{\mathbf{\Sigma }}_{\mathbf{\theta },0}}=E\left[ \left( {{\mathbf{\theta }}_{0}}-\left\langle {{\mathbf{\theta }}_{0}} \right\rangle \right){{\left( {{\mathbf{\theta }}_{0}}-\left\langle {{\mathbf{\theta }}_{0}} \right\rangle \right)}^{T}} \right]$

（2）状态估计

①计算Sigma点

$\mathbf{\chi }_{k-1}^{0}=\left\langle {{\mathbf{\theta }}_{k-1}} \right\rangle ,i=0$

$\mathbf{\chi }_{k-1}^{i}=\left\langle {{\mathbf{\theta }}_{k-1}} \right\rangle +{{\left( \sqrt{(n+\lambda )\cdot {{\Sigma }_{\theta ,k-1}}} \right)}_{i}},i=1,...,n$

$\mathbf{\chi }_{k-1}^{i}=\left\langle {{\mathbf{\theta }}_{k-1}} \right\rangle -{{\left( \sqrt{(n+\lambda )\cdot {{\Sigma }_{\theta ,k-1}}} \right)}_{i}},i=n+1,...,2n$

②时间传播方程

$\mathbf{\chi }_{k|k-1}^{i}=f\left( \mathbf{\chi }_{k-1}^{i} \right)$

$\theta _{k}^{'}=\sum\limits_{i=0}^{2n}{W_{i}^{(m)}\mathbf{\chi }_{k|k-1}^{i}}$

$\mathbf{\Sigma }_{\mathbf{\theta },k}^{'}=\sum\limits_{i=0}^{2n}{W_{i}^{(c)}\left( \mathbf{\chi }_{k|k-1}^{i}-\mathbf{\theta }_{k}^{'} \right){{\left( \mathbf{\chi }_{k|k-1}^{i}-\mathbf{\theta }_{k}^{'} \right)}^{T}}}+{{\mathbf{Q}}}$

$\mathbf{\gamma }_{k|k-1}^{i}=h\left( \mathbf{\chi }_{k|k-1}^{i} \right)$

$\mathbf{z}_{k}^{'}=\sum\limits_{i=0}^{2n}{W_{i}^{(m)}\mathbf{\gamma }_{k|k-1}^{i}}$

③状态更新方程

${{\mathbf{\Sigma }}_{\mathbf{z},k}}=\sum\limits_{i=0}^{2n}{W_{i}^{(c)}\left( \mathbf{\gamma }_{k|k-1}^{i}-\mathbf{z}_{k}^{'} \right){{\left( \mathbf{\gamma }_{k|k-1}^{i}-\mathbf{z}_{k}^{'} \right)}^{T}}}+{{\mathbf{R}}}$

${{\mathbf{\Sigma }}_{\mathbf{\theta z},k}}=\sum\limits_{i=0}^{2n}{W_{i}^{(c)}\left( \mathbf{\chi }_{k|k-1}^{i}-\mathbf{\theta }_{k}^{'} \right){{\left( \mathbf{\gamma }_{k|k-1}^{i}-\mathbf{z}_{k}^{'} \right)}^{T}}}$

${{\mathbf{K}}_{k}}={{\mathbf{\Sigma }}_{\mathbf{\theta z},k}}\cdot \mathbf{\Sigma }_{\mathbf{z},k}^{-1}$

$\left\langle {{\mathbf{\theta }}_{k}} \right\rangle =\mathbf{\theta }_{k}^{'}+{{\mathbf{K}}_{k}}({{\mathbf{z}}_{k}}-\mathbf{z}_{k}^{'})$

${{\mathbf{\Sigma }}_{\mathbf{\theta },k}}=\mathbf{\Sigma }_{\mathbf{\theta },k}^{'}-{{\mathbf{K}}_{k}}{{\mathbf{\Sigma }}_{\mathbf{z},k}}\mathbf{K}_{k}^{T}$

以上就是简化UKF滤波算法的全部过程。

3.2 扩维UKF滤波算法（噪声隐含）

系统的状态转移方程和观测方程为

${{\mathbf{\theta }}_{k}}=f({{\mathbf{\theta }}_{k-1}},{{\mathbf{s}}_{k}})$ ， $\small {{\mathbf{s}}_{k}}\sim \mathcal{N}(0,\mathbf{Q})$

${{\mathbf{z}}_{k}}=h({{\mathbf{\theta }}_{k}},{{\mathbf{v}}_{k}})$ ， $\small {{\mathbf{v}}_{k}}\sim \mathcal{N}(0,\mathbf{R})$

此时需要对状态变量进行扩展，得到增广状态向量

${{\mathbf{\theta }}_{a,k}}=\left[ {{\mathbf{\theta }}_{k}};{{\mathbf{s}}_{k}};{{\mathbf{v}}_{k}} \right]$

增广状态的均值和协方差矩阵分别为

$\left\langle {{\mathbf{\theta }}_{a,k}} \right\rangle =\left[ \left\langle {{\mathbf{\theta }}_{k}} \right\rangle ;{{\mathbf{0}}_{m\times 1}};{{\mathbf{0}}_{l\times 1}} \right]$

${{\mathbf{\Sigma }}_{\mathbf{a},k}}=\left[ \begin{matrix} {{\mathbf{\Sigma }}_{\mathbf{\theta },k}} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{Q} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{R} \\ \end{matrix} \right]$

其中，分别表示状态噪声和观测噪声的维度。

扩维UKF滤波算法的流程为：

（1）初始化

$\left\langle {{\mathbf{\theta }}_{0}} \right\rangle =E\left[ {{\mathbf{\theta }}_{0}} \right]$

$\left\langle {{\mathbf{\theta }}_{\mathbf{a},0}} \right\rangle =E\left[ \left\langle {{\mathbf{\theta }}_{0}} \right\rangle ;{{\mathbf{0}}_{m\times 1}};{{\mathbf{0}}_{l\times 1}} \right]$

${{\mathbf{\Sigma }}_{\mathbf{a},0}}=\left[ \begin{matrix} {{\mathbf{\Sigma }}_{\mathbf{\theta },0}} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{Q} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{R} \\ \end{matrix} \right]$

（2）状态估计

①计算Sigma点

$\mathbf{\chi }_{a,k-1}^{0}=\left\langle {{\mathbf{\theta }}_{a,k-1}} \right\rangle ,i=0$

$\mathbf{\chi }_{a,k-1}^{i}=\left\langle {{\mathbf{\theta }}_{a,k-1}} \right\rangle +{{\left( \sqrt{(n+\lambda )\cdot {{\Sigma }_{a,k-1}}} \right)}_{i}},i=1,...,N$

$\mathbf{\chi }_{a,k-1}^{i}=\left\langle {{\mathbf{\theta }}_{a,k-1}} \right\rangle -{{\left( \sqrt{(n+\lambda )\cdot {{\Sigma }_{a,k-1}}} \right)}_{i}},i=N+1,...,2N$

表示增广状态的维度。

${{\mathbf{\chi }}_{\mathbf{a},k}}={{\left[ \mathbf{\chi }_{\mathbf{\theta },k}^{T},\mathbf{\chi }_{\mathbf{s},k}^{T},\mathbf{\chi }_{\mathbf{v},k}^{T} \right]}^{T}}$

②时间传播方程

$\mathbf{\chi }_{\mathbf{\theta },k|k-1}^{i}=f\left( \mathbf{\chi }_{\mathbf{\theta },k-1}^{i},\mathbf{\chi }_{\mathbf{s},k-1}^{i} \right)$

$\theta _{k}^{'}=\sum\limits_{i=0}^{2N}{W_{i}^{(m)}\mathbf{\chi }_{{\theta },k|k-1}^{i}}$

$\mathbf{\Sigma }_{\mathbf{\theta },k}^{'}=\sum\limits_{i=0}^{2N}{W_{i}^{(c)}\left( \mathbf{\chi }_{\mathbf{\theta },k|k-1}^{i}-\mathbf{\theta }_{\mathbf{a},k}^{'} \right){{\left( \mathbf{\chi }_{\mathbf{a},k|k-1}^{i}-\mathbf{\theta }_{\mathbf{a},k}^{'} \right)}^{T}}}$

$\mathbf{\gamma }_{k|k-1}^{i}=h\left( \mathbf{\chi }_{\mathbf{\theta },k|k-1}^{i},\mathbf{\chi }_{\mathbf{v},k-1}^{i} \right)$

$\mathbf{z}_{k}^{'}=\sum\limits_{i=0}^{2N}{W_{i}^{(m)}\mathbf{\gamma }_{k|k-1}^{i}}$

③状态更新方程

${{\mathbf{\Sigma }}_{\mathbf{z},k}}=\sum\limits_{i=0}^{2N}{W_{i}^{(c)}\left( \mathbf{\gamma }_{k|k-1}^{i}-\mathbf{z}_{k}^{'} \right){{\left( \mathbf{\gamma }_{k|k-1}^{i}-\mathbf{z}_{k}^{'} \right)}^{T}}}$

${{\mathbf{\Sigma }}_{\mathbf{\theta z},k}}=\sum\limits_{i=0}^{2N}{W_{i}^{(c)}\left( \mathbf{\chi }_{\theta ,k|k-1}^{i}-\mathbf{\theta }_{k}^{'} \right){{\left( \mathbf{\gamma }_{k|k-1}^{i}-\mathbf{z}_{k}^{'} \right)}^{T}}}$

${{\mathbf{K}}_{k}}={{\mathbf{\Sigma }}_{\mathbf{\theta z},k}}\cdot \mathbf{\Sigma }_{\mathbf{z},k}^{-1}$

$\left\langle {{\mathbf{\theta }}_{k}} \right\rangle =\mathbf{\theta }_{k}^{'}+{{\mathbf{K}}_{k}}({{\mathbf{z}}_{k}}-\mathbf{z}_{k}^{'})$

${{\mathbf{\Sigma }}_{\mathbf{\theta },k}}=\mathbf{\Sigma }_{\mathbf{\theta },k}^{'}-{{\mathbf{K}}_{k}}{{\mathbf{\Sigma }}_{\mathbf{z},k}}\mathbf{K}_{k}^{T}$

以上就是扩维UKF滤波算法的全部过程。

3.3 两类UKF算法比较

根据以上两个小节的内容，简化UKF算法的Sigma点数为,而扩维UKF算法的Sigma点数为。可见，处理加性噪声的简化UKF的Sigma点较处理隐含噪声的扩维UKF要少许多，因此计算量也要更少。

4 实际应用

现在我们假设在海上有一艘正在做匀速直线运动的船只，其相对于传感器的横纵坐标为 $(x;y;v_{x};v_{y})$ 为隐藏状态，无法直接获得，而传感器可以测量得到船只相对于传感器的距离和角度 $\small (r;\theta)$ ，传感器采样的时间间隔为 $\Delta t$ ，则：

状态向量 $\small (x;y;v_{x};v_{y})$ ，观测向量 $\small (r;\theta)$

状态转移方程和观测方程为：

$\left[ \begin{matrix} {{x}_{k}} \\ {{y}_{k}} \\ {{v}_{xk}} \\ {{v}_{yk}} \\ \end{matrix} \right]=f(\left[ \begin{matrix} {{x}_{k-1}} \\ {{y}_{k-1}} \\ {{v}_{{{x}_{k-1}}}} \\ {{v}_{{{y}_{k-1}}}} \\ \end{matrix} \right])+{{\mathbf{s}}_{k}}=\left[ \begin{matrix} 1 & 0 & \Delta t & 0 \\ 0 & 1 & 0 & \Delta t \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]\left[ \begin{matrix} {{x}_{k-1}} \\ {{y}_{k-1}} \\ {{v}_{{{x}_{k-1}}}} \\ {{v}_{{{y}_{k-1}}}} \\ \end{matrix} \right]+{{\mathbf{s}}_{k}}$

$\left[ \begin{matrix} {{r}_{k}} \\ {{\theta }_{k}} \\ \end{matrix} \right]=h(\left[ \begin{matrix} {{x}_{k}} \\ {{y}_{k}} \\ {{v}_{xk}} \\ {{v}_{yk}} \\ \end{matrix} \right])+{{\mathbf{v}}_{k}}=\left[ \begin{matrix} \sqrt{x_{k}^{2}+x_{y}^{2}} \\ \arctan \frac{{{y}_{k}}}{{{x}_{k}}} \\ \end{matrix} \right]+{{\mathbf{v}}_{k}}$

这里给定距离传感器的噪声均值为，方差为；角度传感器的噪声均值为，方差为（单位弧度）；

采样时间点为个， $\alpha =0.01$ ， $\kappa=0$ ， $\beta =2$ ；

船只的初始状态为，四个状态量的噪声的方差分别为。仿真结果如下：

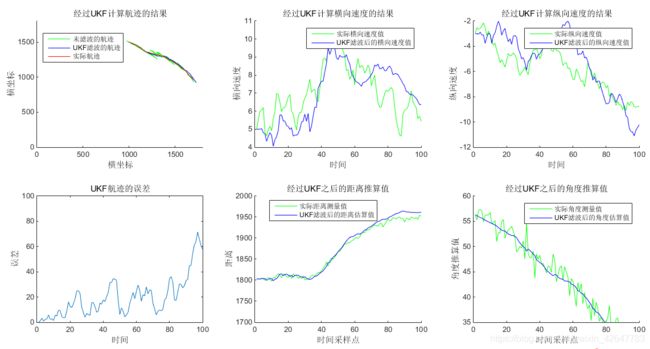
从仿真结果可以看出，UKF在这种情形下的滤波效果还是不错的，相比于PF滤波，UKF能更快地跟踪到目标，即收敛速度更快，而且计算的速度几乎跟EKF是一个量级的。但是在实际应用中，对于船只运动的状态转移噪声的均值 $\mathbf q$ 和协方差矩阵 $\mathbf Q$ ，以及传感器的观测噪声的均值 $\mathbf r$ 和协方差矩阵 $\mathbf R$ ，往往都是未知的，有很多情况都只有观测值而已，这样的情形下，就有必要利用观测值对噪声的统计量参数做出适当的估计（学习）。

5 参数估计（学习）

利用EM算法和极大后验概率估计（MAP），对未知的噪声参数做出估计，再利用估计出的参数去递推卡尔曼滤波的解。本文对EM算法在卡尔曼滤波框架中的推导暂时先不给出，之后可能会补充，这里就先给出一种Adaptive-UKF算法的公式。

${{\mathbf{\theta }}_{k}}=f({{\mathbf{\theta }}_{k-1}})+{{\mathbf{s}}_{k}}$ ， ${{\mathbf{s}}_{k}}\sim \mathcal{N}(\mathbf{q},\mathbf{Q})$

${{\mathbf{z}}_{k}}=h({{\mathbf{\theta }}_{k}})+{{\mathbf{v}}_{k}}$ ， ${{\mathbf{v}}_{k}}\sim \mathcal{N}(\mathbf{r},\mathbf{R})$

利用递推的方法：

${{\mathbf{\hat{q}}}_{k+1}}=(1-{{d}_{k+1}}){{\mathbf{\hat{q}}}_{k}}+{{d}_{k+1}}\left[ \left\langle {{\mathbf{\theta }}_{k+1}} \right\rangle -\sum\limits_{i=0}^{2n}{W_{i}^{(m)}f(\mathbf{\chi }_{k}^{i})} \right]$

${{\mathbf{\hat{Q}}}_{k+1}}=(1-{{d}_{k+1}}){{\mathbf{\hat{Q}}}_{k}}+{{d}_{k+1}}\left[ {{\mathbf{K}}_{k+1}}{{\mathbf{e}}_{k+1}}\mathbf{e}_{k+1}^{T}\mathbf{K}_{k+1}^{T}+{{\mathbf{\Sigma }}_{k+1}} \right]$

${{\mathbf{\hat{r}}}_{k+1}}=(1-{{d}_{k+1}}){{\mathbf{\hat{r}}}_{k}}+{{d}_{k+1}}\left[ {{z}_{k+1}}-\sum\limits_{i=0}^{2n}{W_{i}^{(m)}h(\mathbf{\chi }_{k+1|k}^{i})} \right]$

${{\mathbf{\hat{R}}}_{k+1}}=(1-{{d}_{k+1}}){{\mathbf{\hat{R}}}_{k}}+{{d}_{k+1}}{{\mathbf{e}}_{k+1}}\mathbf{e}_{k+1}^{T}$

其中，

${{\mathbf{e}}_{k}}={{\mathbf{z}}_{k}}-\mathbf{z}_{k}^{'}$

${{d}_{k+1}}=\frac{1-b}{1-{{b}^{k+1}}}$

的取值一般为。

初始的 ${{\mathbf{\hat{Q}}}_{0}}$ ， ${{\mathbf{\hat{R}}}_{0}}$ ， ${{\mathbf{\hat{q}}}_{0}}$ 和 ${{\mathbf{\hat{r}}}_{0}}$ 可以设置为任意较小值，然后每做完一轮UKF滤波，就可以更新一次参数，用于下一轮的UKF滤波。利用以上的Adaptive-UKF算法对船只的运动做滤波跟踪，得到的效果如下图所示：

相比于没有做参数估计的UKF滤波，可以看出，Adaptive-UKF在估计误差上与UKF滤波相差不大，而且，它并不需要指定状态转移噪声和观测噪声的参数，将更有利于在实际中的应用。

6 总结

从整体上看，UKF滤波算法是一个比较优秀的信号滤波与跟踪算法，通过把UT变换应用到卡尔曼滤波框架中，使得不需要计算Jacobi矩阵，不必对非线性函数做任何形式的逼近，即使系统函数不连续，也可以获得不错的滤波性能。而且，UKF对于随机状态的分布不一定要求是高斯分布的，因此UKF具有非常广泛的应用。

UKF与EKF的重要差异是EKF是对高度复杂非线性系统模型函数进行泰勒展开，对展开式进行一阶线性截断处理，这样便可将模型转化为计算机处理的线性问题，然后进行卡尔曼滤波，因此EKF是一种次优滤波，但由于考虑了泰勒级数的展开，因此大大增加了运算量。与对非线性函数的近似相比，高斯分布的近似要简单得多。UKF能获得精确到三阶矩均值和协方差，具有更高的滤波精度，而其计算量仍然与EKF同阶，并且该方法直接使用系统的非线性模型，不需对非线性系统线性化，也不需要像二次滤波那样计算Hession和Jacobi矩阵，提高了运算速度，对线性系统两个具有相同的估计性能。总体来说，对非线性系统，UKF具有更高的滤波精度和稳定性。

7 参考文献

[1] S. Peng, C. Chen, H. Shi and Z. Yao, "State of Charge Estimation of Battery Energy Storage Systems Based on Adaptive Unscented Kalman Filter With a Noise Statistics Estimator," in IEEE Access, vol. 5, pp. 13202-13212, 2017.

[2] 卡尔曼滤波系列——（一）标准卡尔曼滤波.

[3] 卡尔曼滤波系列——（二）扩展卡尔曼滤波.

[4] 卡尔曼滤波系列——（三）粒子滤波（重写）

[5] https://max.book118.com/html/2017/0502/103920556.shtm.

原创性声明：本文属于作者原创性文章，小弟码字辛苦，转载还请注明出处。谢谢~

如果有哪些地方表述的不够得体和清晰，有存在的任何问题，亦或者程序存在任何考虑不周和漏洞，欢迎评论和指正，谢谢各路大佬。

需要代码和有需要相关技术支持的可咨询QQ：297461921

Matlab2024a安装教程是阿宇呢信息可视化开发语言
MATLAB是一款商业数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，主要包括MATLAB和Simulink两大部分，可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等，主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。1.解压安装包：①鼠标右击【MATLABR2024a(64bit)
【图像压缩】奇异值分解SVD灰色图像压缩（可设置压缩比）【含Matlab源码 4358期】 Matlab武动乾坤 Matlab图像处理（进阶版）matlab
✅博主简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，Matlab项目合作可私信。个人主页：海神之光代码获取方式：海神之光Matlab王者学习之路—代码获取方式⛳️座右铭：行百里者，半于九十。更多Matlab仿真内容点击Matlab图像处理（进阶版）路径规划（Matlab）神经网络预测与分类（Matlab）优化求解（Matlab）语音处理（Matlab）信号处理（Matlab）车间调度
微控制器和微处理器的区别（含课本原图）嵌入式Linux系统开发嵌入式单片机硬件 MCU CPU MPU 微控制器微处理器
微控制器：CPU+片内内存+片内外设微处理器：CPU处理器通常指微处理器、微控制器和数字信号处理器这三种类型的芯片。微处理器（MPU）通常代表一个功能强大的CPU,但不是为任何已有的特定计算目的而设计的芯片。这种芯片往往是个人计算机和高端工作站的核心CPU。最常见的微处理器是Motorola的68K系列和Intel的X86系列。早期的微控制器是将一个计算机集成到一个芯片中,实现嵌入式应用,故称单片
基于深度学习的信号滤波：创新技术与应用挑战逼子歌深度学习神经网络信号滤波图像去噪卷积神经网络长短期记忆网络
一、引言1.1研究背景随着科技的不断发展，信号处理领域面临着越来越复杂的挑战。在众多信号处理技术中，基于深度学习的信号滤波技术逐渐崭露头角，成为研究的热点。基于深度学习的信号滤波在信号处理领域具有至关重要的地位。如今，我们生活在一个数据爆炸的时代，各种信号源不断产生大量的复杂数据。例如，在通信领域，信号常常受到噪声干扰，传统的滤波方法在处理复杂、非线性信号时可能效果不佳。而深度学习技术具有自动特征
matlab cdf,Matlab 简单计算PDF和CDF | 学步园苏晓晓 matlab cdf
通信的魅力就是在于随机性中蕴含的确定性，这也就是为什么你随便拿出一本通信方面的教材，前面几章都会大篇幅的讲解随机过程，随机过程也是研究生必须深入了解的一门课，特别是对于信号处理以及通信专业的学生。在实际工作中，通常会得到很多随机的数，我们要分析它们的分布，最常见的就是用PDF和CDF来描述了。好了，还是举出一个具体例子吧。那么实际中我们要验证是不是符合这样的分布，首先看代码再解释：%%%%%%%%
使用matlab的热门问题七十二五值得关注 matlab 开发语言青少年编程算法经验分享
MATLAB广泛应用于科学计算、数据分析、信号处理、图像处理、机器学习等多个领域，因此热门问题也涵盖了这些方面。以下是一些可能被认为当前最热门的MATLAB问题：深度学习与神经网络：如何使用MATLAB的深度学习工具箱（DeepLearningToolbox）来构建和训练神经网络？如何利用MATLAB进行图像识别、语音识别或自然语言处理等深度学习应用？数据分析与可视化：如何使用MATLAB进行大数
gd32 定时器时钟_GD32E5 系列定时器全面助力工业互联网 weixin_39861054 gd32 定时器时钟
业界领先的半导体供应商兆易创新GigaDevice(股票代码603986)正式发布基于全新Arm®Cortex®-M33内核的GD32E5系列高性能微控制器。这系列MCU采用台积电低功耗40纳米(40nm)嵌入式闪存工艺构建，具备业界领先的处理能力、功耗效率、连接特性和更经济的开发成本，进一步推动嵌入式开发向高精度工业控制领域扩展，解决数字电源、电机变频、测量仪器、混合信号处理、高端消费类应用等多
大厂嵌入式数字信号处理器(DSP)面试题及参考答案大模型大数据攻城狮单片机嵌入式面试模数装换器离散信号信号处理滤波器嵌入式芯片
什么是模拟信号处理和数字信号处理（DSP）在嵌入式系统中的应用？模拟信号处理是对连续变化的模拟信号进行操作和处理。在嵌入式系统中，模拟信号处理的应用包括传感器信号的调理，例如温度传感器、压力传感器等输出的模拟信号通常比较微弱且可能受到噪声干扰，需要通过放大器进行放大，通过滤波器去除噪声等操作，使其能够被后续的模数转换电路准确地转换为数字信号。数字信号处理（DSP）则是对离散的数字信号进行各种算法处
EI检索-机器视觉、图像处理与影像技术国际学术会议（MVIPIT 2023）邀您参会！诗远Yolanda 图像处理人工智能计算机视觉
机器视觉是计算机学科的一个重要分支，它综合了光学、机械、电子、计算机软硬件等方面的技术，涉及到计算机、图像处理、模式识别、人工智能、信号处理、光机电一体化等多个领域。而图像处理等技术的快速发展也推动了机器视觉的发展。机器视觉在我国具有广泛的工业应用，核心功能包括：测量，检测，识别，定位等。第一届机器视觉、图像处理与影像技术国际学术会议（MVIPIT2023）将于2023年7月26日-28日在浙江杭
TCP 通信程序示例——实现一个服务器连接多个客户端求学者1.0 linux 学习 c语言网络协议
tcp_fork#include#include#include#include#include/*SeeNOTES*/#include#include#include#include#include#include#include//定义一个类型别名，方便后续使用typedefstructsockaddr*(SA);//信号处理函数，用于处理子进程结束的信号voidhandle(intnum){
Python librosa模块介绍骚火棍人生苦短我用Python librosa
librosa语音信号处理模块参考链接：https://www.cnblogs.com/LXP-Never/p/11561355.html
TMS320F2812原理与开发：深入解析与实践指南蓝虫虫
本文还有配套的精品资源，点击获取简介：苏奎峰编著的《TMS320F2812原理与开发》全面讲解了德州仪器的TMS320F2812数字信号处理器。本书详细阐述了TMS320F2812的架构、指令系统、外设功能，并介绍了其在工业控制、电力电子、自动化、通信等领域的应用。书中详述了如何配置控制芯片各部分、编写高效DSP程序，并使用TI的开发工具进行系统级设计。1.TMS320F2812数字信号处理器原理
arm a7 支持虚拟化吗_Arm增加CPU、GPU和ISP，实现自主和视觉安全_Mali weixin_39569112 arm a7 支持虚拟化吗 GPU 编程 CPU 异同点 nas918+支持的cpu 用ARM编写显示当前系统时间
原标题：Arm增加CPU、GPU和ISP，实现自主和视觉安全Arm引入了一套新的知识产权(IP)，包括新的CPU、GPU和ISP(图像信号处理器)，以实现可扩展、高效的计算能力，以实现跨汽车和工业应用的安全、自主决策。新的IP套件包括ArmCortex-A78AECPU、ArmMali-G78AEGPU和ArmMali-C71AEISP，所有这些都是为了使硅供应商和OEM能够设计为自主工作负载。这
ISP(图像信号处理器)是什么？ FoGoiN 嵌入式硬件单片机物联网
由于刚接触到开发版，认识到了图像处理器（imageprocessor）,又名imageprocessingengine,imageprocessingunit(IPU),imagesignalprocessor(ISP)。和电脑的GPU类似，通常采并行计算。功能：Bayertransformation图像传感器（就是光电转换器）中的光电二极管（吸收光子产生电流）其实是无法识别颜色的，为了能够识别颜
什么是奈奎斯特采样定理达西西66 奈奎斯特采样定理
奈奎斯特采样定理，也被称为奈奎斯特定理或奈氏定理，是信号处理领域中至关重要的原理之一。它揭示了在数字信号处理中如何正确地采样模拟信号，以避免信息丢失和混叠现象。本文将深入探讨奈奎斯特采样定理的原理、应用和实例，以及其在通信、音频处理和图像处理等领域的重要性。奈奎斯特采样定理的基本原理奈奎斯特采样定理是由美国工程师哈里·S·奈奎斯特（HarryNyquist）在20世纪20年代提出的。该定理的核心思
matlab 发射随机信号,matlab随机信号处理刚下拖拉机 matlab 发射随机信号
matlab中rand和randn是产生随机数的命令，x=rand(1,N)产生(0，1)区间均匀分布的长度为N的随机信号，x=randn(1,N)产生长度为N且具有零均值和单位方差的正态分布的随机信号。matlab中产生伪随机数需要种子，把不同的种子用于不同的随机数生成器产生不同的伪随机数。betarnd贝塔分布的随机数生成器binornd二项分布的随机数生成器chi2rnd卡方分布的随机数生成
宠心宝智能居家监测器萌宠心语宠物人工智能科技生活
在智能家居生态中，宠物健康管理正变得越来越智能化和精细化。智能听诊器作为这一领域的创新设备，为宠物提供了更高质量的生活保障。智能听诊器通过高精度传感器捕捉宠物胸腔表面的微小振动，这些振动主要由心脏和肺部的运作产生。利用数字信号处理技术，智能听诊器能够过滤和增强原始信号，提取出清晰的心音和肺音。通过算法分析，智能听诊器能够识别出心率、呼吸频率等关键健康指标，为宠物主人提供了一个科学、精准的健康管理工
基于Matlab与Simulink实现100种仿真案例（附上案例源码） Matlab仿真实验室 Matlab仿真实验1000例 matlab 开发语言 Simulink 100种仿真案例数学建模
文章目录1.介绍2.案例源码下载1.介绍MATLAB和Simulink是适用于科学计算和工程设计的强大工具。MATLAB是一种高级编程语言，主要用于数值计算和数据分析，而Simulink则是一种基于模型的设计和仿真环境，用于开发和测试控制系统、信号处理和通信系统等。MATLAB的优点之一是其丰富的库和工具箱。这些库和工具箱包括数值计算、统计分析、图像处理、信号处理、控制系统等。这使得MATLAB成
fpga图像处理实战-中值滤波梦梦梦梦子~ OV5640+图像处理图像处理 fpga开发计算机视觉
中值滤波中值滤波算法是一种常用的非线性数字滤波技术，主要用于信号处理和图像处理领域。其核心思想是使用信号或图像中某个窗口内所有数值的中值来替换该窗口中心的值，从而达到消除噪声、保留边缘细节的目的。原理简介中值滤波的基本原理是将每个像素点的值用其邻域内的中值来代替，这样可以将孤立的噪声点替换为更接近真实值的周围像素值，从而达到平滑图像的目的。FPGA实现`timescale1ns/1ps////Co
数学基础 -- 线性代数之酉矩阵 sz66cm 量子计算线性代数
酉矩阵（UnitaryMatrix）酉矩阵是线性代数中一种重要的矩阵类型，特别在量子力学和信号处理等领域有广泛的应用。以下是酉矩阵的定义、性质以及使用和计算的例子。1.定义酉矩阵是一个复矩阵UUU，满足以下条件：U†U=UU†=IU^{\dagger}U=UU^{\dagger}=IU†U=UU†=I其中：U†U^{\dagger}U†是矩阵UUU的共轭转置矩阵，即UUU的转置矩阵再取元素的共轭。
重头开始嵌入式第二十七天（Linux系统编程信号通信） FLPGYH Linux系统高级编程 c语言 linux vim
目录进程间通信===》1.信号通信1.信号的五种类型：2.kill1、信号kill-l==>前32个有具体含义的信号3.信号注册函数原型：1.自定义信号处理：2、在所有的信号中有如下两个特列：2.共享内存信号量集1.key创建方式有三种：共享内存===》效率最高的进程间通信方式1、申请对象：2.映射对象：shmat()3.读写共享内存：类似堆区内存的直接读写：4.撤销映射：shmdt5.删除对象：
【LSTM分类】基于贝叶斯优化卷积神经网络结合长短时记忆BO-CNN-LSTM实现柴油机故障诊断含Matlab源码 matlab科研助手 lstm 分类 cnn
✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，代码获取、论文复现及科研仿真合作可私信。个人主页：Matlab科研工作室个人信条：格物致知。更多Matlab完整代码及仿真定制内容点击智能优化算法神经网络预测雷达通信无线传感器电力系统信号处理图像处理路径规划元胞自动机无人机物理应用机器学习内容介绍柴油机作为重要的动力设备，其运行状态的可靠性直接影响着生产效率和安全。及时准确地诊断柴
系统环境介绍薄荷364 linux ubuntu
操作系统课程介绍：系统环境：介绍系统简介、库文件、环境变量、编译器、系统特性内存管理：操作系统是如何管理内存的文件管理：文件读写、目录读写、文件属性、文件管理信号处理：多个程序同时运行、解决一些通信类的问题进程管理：多个程序同时运行、解决一些复杂问题进程通信：多个进程需要协同交互数据，这是多进程协同工作的基础线程管理：让一个程序同时做若干个任务线程同步：让多个线程同时工作时不相互干扰、破坏一、UN
操作系统---线程管理薄荷364 linux ubuntu
一、线程介绍什么是线程：线程是操作系统能内够进行运算、执行的最小单位，它被包含在进程之中，是进程中的实际运作单位。一条线程指的是进程中一个单一顺序的控制流，一个进程中可以并发多个线程，每条线程并行执行不同的任务。总结：线程是进程的一部分，是进程内负责执行的单位，进程是由资源单位（内存资源、信号处理方案、文件表）+执行单位组成，默认情况下进程内只有一个线程，但可以有多个。线程的发展简史：60年代，在
EI级 | Matlab实现TCN-LSTM-MATT、TCN-LSTM、TCN、LSTM多变量时间序列预测对比天天Matlab代码科研顾问 matlab lstm 开发语言
✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，代码获取、论文复现及科研仿真合作可私信。个人主页：Matlab科研工作室个人信条：格物致知。更多Matlab完整代码及仿真定制内容点击智能优化算法神经网络预测雷达通信无线传感器电力系统信号处理图像处理路径规划元胞自动机无人机内容介绍风电作为一种清洁、可再生能源，近年来得到了快速发展。准确预测风电功率输出对于提高风电场运行效率，优化电
C语言信号编程深入研究极客代码玩转C语言开发语言 c语言
信号是操作系统向进程发送的一种软件中断，用于通知进程发生了某种特殊情况或异常事件。本篇文章将详细介绍如何使用C语言处理信号，包括基本的信号处理、自定义信号处理函数以及一些高级主题。1.引言信号处理是操作系统与进程之间的一种通信机制。在C语言中，信号处理通常涉及捕获特定信号并在程序中执行相应的处理动作。本指南旨在提供一个全面的框架，帮助读者深入了解信号处理的基本原理和实践技巧。2.信号基础2.1信号
【Python系列】signal信号处理 Kwan的解忧杂货铺@新空间代码工作室 s2 Python python 信号处理开发语言
欢迎来到我的博客，很高兴能够在这里和您见面！希望您在这里可以感受到一份轻松愉快的氛围，不仅可以获得有趣的内容和知识，也可以畅所欲言、分享您的想法和见解。推荐:kwan的首页,持续学习,不断总结,共同进步,活到老学到老导航檀越剑指大厂系列:全面总结java核心技术,jvm,并发编程redis,kafka,Spring,微服务等常用开发工具系列:常用的开发工具,IDEA,Mac,Alfred,Git,
巴伦射频变器（Balun RF Transformer）的常规产品通常包括以下几种类型 Hqst88888 网络
1:1高频变压器：用于将平衡和非平衡信号进行转换，通常在信号传输和接收电路中使用，如无线通信设备和各种高频电子设备中。1:4高频变压器：主要用于阻抗匹配和信号传输，能够将低阻抗的平衡信号转换为高阻抗的非平衡信号，广泛应用于射频收发器件和天线系统。双平衡变压器：用于同时处理两个平衡信号的变压器，如应用于差分放大器和差分信号处理电路中。4:1高频变压器：类似于1:4变压器，用于信号匹配和转换，将高阻抗
Linux进程间通信：信号(signal) D.• Linux进程通信 Linux进程 c语言 c++开发语言 linux 服务器
目录信号说明一信号发送①raise函数②kill函数③alarm函数二信号接收while函数：sleep函数：pause函数：三信号处理signal函数信号说明在Linux中，①信号可以简单理解为软中断，许多重要的程序都需要处理信号。信号，为Linux提供了一种处理异步事件的方法。比如，终端用户输入了ctrl+c来中断程序，会通过信号机制停止一个程序。②信号也是进程间通信的一种方式，也是如此，进程
产品推荐 | 基于VU13P FPGA的4路FMC接口基带信号处理平台迪普微社区产品推荐 fpga开发信号处理 fpga 图像处理无线电 FMC
一、产品概述TES641是一款基于VirtexUltraScale+系列FPGA的高性能4路FMC接口基带信号处理平台，该平台采用1片Xilinx的VirtexUltraScale+系列FPGAXCVU13P作为信号实时处理单元，该板卡具有4个FMC子卡接口（其中有2个为FMC+接口），各个节点之间通过高速串行总线进行互联，该FPGA支持最大32Gbps的高速串行总线，适用于100G以太网、JES
Hadoop(一) 朱辉辉33 hadoop linux
今天在诺基亚第一天开始培训大数据，因为之前没接触过Linux，所以这次一起学了，任务量还是蛮大的。首先下载安装了Xshell软件，然后公司给了账号密码连接上了河南郑州那边的服务器，接下来开始按照给的资料学习，全英文的，头也不讲解，说锻炼我们的学习能力，然后就开始跌跌撞撞的自学。这里写部分已经运行成功的代码吧. 在hdfs下，运行hadoop fs -mkdir /u
maven An error occurred while filtering resources blackproof maven 报错
转：http://stackoverflow.com/questions/18145774/eclipse-an-error-occurred-while-filtering-resources maven报错： maven An error occurred while filtering resources Maven -> Update Proje
jdk常用故障排查命令 daysinsun jvm
linux下常见定位命令： 1、jps 输出Java进程 -q 只输出进程ID的名称，省略主类的名称； -m 输出进程启动时传递给main函数的参数； &nb
java 位移运算与乘法运算周凡杨 java 位移运算乘法
对于 JAVA 编程中，适当的采用位移运算，会减少代码的运行时间，提高项目的运行效率。这个可以从一道面试题说起：问题：用最有效率的方法算出2 乘以8 等於几?” 答案：2 << 3 由此就引发了我的思考，为什么位移运算会比乘法运算更快呢？其实简单的想想，计算机的内存是用由 0 和 1 组成的二
java中的枚举(enmu) g21121 java
从jdk1.5开始，java增加了enum(枚举)这个类型，但是大家在平时运用中还是比较少用到枚举的，而且很多人和我一样对枚举一知半解，下面就跟大家一起学习下enmu枚举。先看一个最简单的枚举类型，一个返回类型的枚举： public enum ResultType { /** * 成功 */ SUCCESS, /** * 失败 */ FAIL,
MQ初级学习 510888780 activemq
1.下载ActiveMQ 去官方网站下载：http://activemq.apache.org/ 2.运行ActiveMQ 解压缩apache-activemq-5.9.0-bin.zip到C盘，然后双击apache-activemq-5.9.0-\bin\activemq-admin.bat运行ActiveMQ程序。启动ActiveMQ以后，登陆：http://localhos
Spring_Transactional_Propagation 布衣凌宇 spring transactional
//事务传播属性 @Transactional(propagation=Propagation.REQUIRED)//如果有事务，那么加入事务，没有的话新创建一个 @Transactional(propagation=Propagation.NOT_SUPPORTED)//这个方法不开启事务 @Transactional(propagation=Propagation.REQUIREDS_N
我的spring学习笔记12-idref与ref的区别 aijuans spring
idref用来将容器内其他bean的id传给<constructor-arg>/<property>元素，同时提供错误验证功能。例如： <bean id ="theTargetBean" class="..." /> <bean id ="theClientBean" class=&quo
Jqplot之折线图 antlove js jquery Web timeseries jqplot
timeseriesChart.html <script type="text/javascript" src="jslib/jquery.min.js"></script> <script type="text/javascript" src="jslib/excanvas.min.js&
JDBC中事务处理应用百合不是茶 java JDBC编程事务控制语句
解释事务的概念; 事务控制是sql语句中的核心之一;事务控制的作用就是保证数据的正常执行与异常之后可以恢复事务常用命令: Commit提交
[转]ConcurrentHashMap Collections.synchronizedMap和Hashtable讨论 bijian1013 java 多线程线程安全 HashMap
在Java类库中出现的第一个关联的集合类是Hashtable，它是JDK1.0的一部分。 Hashtable提供了一种易于使用的、线程安全的、关联的map功能，这当然也是方便的。然而，线程安全性是凭代价换来的――Hashtable的所有方法都是同步的。此时，无竞争的同步会导致可观的性能代价。Hashtable的后继者HashMap是作为JDK1.2中的集合框架的一部分出现的，它通过提供一个不同步的
ng-if与ng-show、ng-hide指令的区别和注意事项 bijian1013 JavaScript AngularJS
angularJS中的ng-show、ng-hide、ng-if指令都可以用来控制dom元素的显示或隐藏。ng-show和ng-hide根据所给表达式的值来显示或隐藏HTML元素。当赋值给ng-show指令的值为false时元素会被隐藏，值为true时元素会显示。ng-hide功能类似，使用方式相反。元素的显示或
【持久化框架MyBatis3七】MyBatis3定义typeHandler bit1129 TypeHandler
什么是typeHandler? typeHandler用于将某个类型的数据映射到表的某一列上，以完成MyBatis列跟某个属性的映射内置typeHandler MyBatis内置了很多typeHandler，这写typeHandler通过org.apache.ibatis.type.TypeHandlerRegistry进行注册，比如对于日期型数据的typeHandler，
上传下载文件rz,sz命令 bitcarter linux命令rz
刚开始使用rz上传和sz下载命令：因为我们是通过secureCRT终端工具进行使用的所以会有上传下载这样的需求：我遇到的问题： sz下载A文件10M左右，没有问题但是将这个文件A再传到另一天服务器上时就出现传不上去，甚至出现乱码，死掉现象，具体问题解决方法：上传命令改为;rz -ybe 下载命令改为：sz -be filename 如果还是有问题：那就是文
通过ngx-lua来统计nginx上的虚拟主机性能数据 ronin47 ngx-lua　统计解禁ip
介绍以前我们为nginx做统计,都是通过对日志的分析来完成.比较麻烦,现在基于ngx_lua插件,开发了实时统计站点状态的脚本,解放生产力.项目主页: https://github.com/skyeydemon/ngx-lua-stats 功能支持分不同虚拟主机统计, 同一个虚拟主机下可以分不同的location统计. 可以统计与query-times request-time
java-68-把数组排成最小的数。一个正整数数组，将它们连接起来排成一个数，输出能排出的所有数字中最小的。例如输入数组{32, 321}，则输出32132 bylijinnan java
import java.util.Arrays; import java.util.Comparator; public class MinNumFromIntArray { /** * Q68输入一个正整数数组，将它们连接起来排成一个数，输出能排出的所有数字中最小的一个。 * 例如输入数组{32, 321}，则输出这两个能排成的最小数字32132。请给出解决问题
Oracle基本操作 ccii Oracle SQL总结 Oracle SQL语法 Oracle基本操作 Oracle SQL
一、表操作 1. 常用数据类型 NUMBER(p,s)：可变长度的数字。p表示整数加小数的最大位数，s为最大小数位数。支持最大精度为38位 NVARCHAR2(size)：变长字符串，最大长度为4000字节（以字符数为单位） VARCHAR2(size)：变长字符串，最大长度为4000字节（以字节数为单位） CHAR(size)：定长字符串，最大长度为2000字节，最小为1字节，默认
[强人工智能]实现强人工智能的路线图 comsci 人工智能
1：创建一个用于记录拓扑网络连接的矩阵数据表 2:自动构造或者人工复制一个包含10万个连接(1000*1000)的流程图 3：将这个流程图导入到矩阵数据表中 4：在矩阵的每个有意义的节点中嵌入一段简单的
给Tomcat，Apache配置gzip压缩(HTTP压缩)功能 cwqcwqmax9 apache
背景： HTTP 压缩可以大大提高浏览网站的速度，它的原理是，在客户端请求网页后，从服务器端将网页文件压缩，再下载到客户端，由客户端的浏览器负责解压缩并浏览。相对于普通的浏览过程HTML ,CSS,Javascript , Text ，它可以节省40%左右的流量。更为重要的是，它可以对动态生成的，包括CGI、PHP , JSP , ASP , Servlet,SHTML等输出的网页也能进行压缩，
SpringMVC and Struts2 dashuaifu struts2 springMVC
SpringMVC VS Struts2 1: spring3开发效率高于struts 2: spring3 mvc可以认为已经100%零配置 3: struts2是类级别的拦截，一个类对应一个request上下文， springmvc是方法级别的拦截，一个方法对应一个request上下文，而方法同时又跟一个url对应所以说从架构本身上 spring3 mvc就容易实现r
windows常用命令行命令 dcj3sjt126com windows cmd command
在windows系统中，点击开始－运行，可以直接输入命令行，快速打开一些原本需要多次点击图标才能打开的界面，如常用的输入cmd打开dos命令行，输入taskmgr打开任务管理器。此处列出了网上搜集到的一些常用命令。winver 检查windows版本 wmimgmt.msc 打开windows管理体系结构(wmi) wupdmgr windows更新程序 wscrip
再看知名应用背后的第三方开源项目 dcj3sjt126com ios
知名应用程序的设计和技术一直都是开发者需要学习的，同样这些应用所使用的开源框架也是不可忽视的一部分。此前《 iOS第三方开源库的吐槽和备忘》中作者ibireme列举了国内多款知名应用所使用的开源框架，并对其中一些框架进行了分析，同样国外开发者 @iOSCowboy也在博客中给我们列出了国外多款知名应用使用的开源框架。另外txx's blog中详细介绍了 Facebook Paper使用的第三
Objective-c单例模式的正确写法 jsntghf 单例 ios iPhone
一般情况下，可能我们写的单例模式是这样的： #import <Foundation/Foundation.h> @interface Downloader : NSObject + (instancetype)sharedDownloader; @end #import "Downloader.h" @implementation
jquery easyui datagrid 加载成功，选中某一行 hae jquery easyui datagrid 数据加载
1.首先你需要设置datagrid的onLoadSuccess $( '#dg' ).datagrid({onLoadSuccess : function (data){ $( '#dg' ).datagrid( 'selectRow' ,3); }}); 2.onL
jQuery用户数字打分评价效果 ini JavaScript html jquery Web css
效果体验：http://hovertree.com/texiao/jquery/5.htmHTML文件代码： <!DOCTYPE html> <html xmlns="http://www.w3.org/1999/xhtml"> <head> <title>jQuery用户数字打分评分代码 - HoverTree</
mybatis的paramType kerryg DAO sql
MyBatis传多个参数： 1、采用#{0},#{1}获得参数： Dao层函数方法： public User selectUser(String name,String area); 对应的Mapper.xml <select id="selectUser" result
centos 7安装mysql5.5 MrLee23 centos
首先centos7 已经不支持mysql，因为收费了你懂得，所以内部集成了mariadb，而安装mysql的话会和mariadb的文件冲突，所以需要先卸载掉mariadb，以下为卸载mariadb，安装mysql的步骤。 #列出所有被安装的rpm package rpm -qa | grep mariadb #卸载 rpm -e mariadb-libs-5.
利用thrift来实现消息群发 qifeifei thrift
Thrift项目一般用来做内部项目接偶用的，还有能跨不同语言的功能，非常方便，一般前端系统和后台server线上都是3个节点，然后前端通过获取client来访问后台server，那么如果是多太server，就是有一个负载均衡的方法，然后最后访问其中一个节点。那么换个思路，能不能发送给所有节点的server呢，如果能就
实现一个sizeof获取Java对象大小 teasp java HotSpot 内存对象大小 sizeof
由于Java的设计者不想让程序员管理和了解内存的使用，我们想要知道一个对象在内存中的大小变得比较困难了。本文提供了可以获取对象的大小的方法，但是由于各个虚拟机在内存使用上可能存在不同，因此该方法不能在各虚拟机上都适用，而是仅在hotspot 32位虚拟机上，或者其它内存管理方式与hotspot 32位虚拟机相同的虚拟机上适用。
SVN错误及处理 xiangqian0505 SVN提交文件时服务器强行关闭
在SVN服务控制台打开资源库“SVN无法读取current” ---摘自网络写道 SVN无法读取current修复方法 Can't read file : End of file found 文件：repository/db/txn_current、repository/db/current 其中current记录当前最新版本号，txn_current记录版本库中版本