图论之最短路算法整理总结
Floyd最短路径算法
1.#include<stdio.h>
2.#define INF 9999999
3.int e[1005][1005];
4.int n,m,a,b,c;
5.void floyd(){
6.for(int k=1; k<=n; k++)
7. for(int j=1; j<=n; j++)
8. for(int i=1; i<=n;i++)
9. if(e[i][j]>e[i][k]+e[k][j])
10. e[i][j]=e[i][k]+e[k][j];
11.}
12.int main(){
13. while(scanf("%d%d",&n,&m) && n && m){
14. for(int i=1; i<=n; i++)
15. for(int j=1; j<=n; j++){
16. if(i==j) e[i][j]=0;
17. else e[i][j]=INF;
18. }
19. while(m--){
20. scanf("%d%d%d",&a,&b,&c);
21. e[a][b]=e[b][a]=c;
22. }
23. floyd();
24. printf("%d\n",e[1][n]);
25. }
26.return 0;
27.}
这个算法是最容易理解的最短路径算法,代码长度也很短
原理上就是枚举计算每个点到另一点的最短路径。还有一个遍历变量k,其中分两种情况,a到b的直接距离,a经过k到达b的距离,这两种情况取最小值,k是除了a和b的任意节点。注意k要在最外层循环,所以这个算法的复杂度是o(n^3),但是优点是容易写,对小图的最短路径可以快速a题
Bellman-ford最短路算法
1.#include"bits/stdc++.h"
2.using namespace std;
3.const int INF =1e6;
4.struct edge{
5. int from,to,value;
6.}e[10005];//记录边的开始和结束,以及权值
7.int n,m,cnt;
8.int pre[105];
9.void bellman (){
10. int s=1;
11. int d[105];//记录当前点到开始点的最短路
12. for(int i=1;i<=n;i++){
13. d[i]=INF;
14. }
15. d[s]=0;
16. for(int k=1;k<=n;k++){//如果没有负权环,最多更新n-1次。
17. for(int i=0;i<cnt;i++){//当前点的暂时最短路是由相邻点的暂时最短路推算出来的,由于是无向图,所以需要两个方向
18. int x=e[i].from,y=e[i].to;
19. if(d[x]>d[y]+e[i].value ){
20. d[x]=d[y]+e[i].value;
21. }
22. }
23. //中间测试代码,方便看d[]的修改情况
24. for(int i=1;i<=n;i++){
25. printf("d[%d]=%d\n",i,d[i]);
26. }
27. printf("----------------------------\n");
28. }
29. printf("%d\n",d[n]);
30.}
31.int main(){
32. while(~scanf("%d%d",&n,&m)){
33. if(n==0&&m==0)return 0;
34. cnt=0;
35. while(m--){
36. int a,b,c;
37. scanf("%d %d %d",&a,&b,&c);
38. e[cnt].from =a;e[cnt].to =b;e[cnt].value =c;cnt++;
39. e[cnt].from =b;e[cnt].to =a;e[cnt].value =c;cnt++;
40. }
41. bellman();
42. }
43.}
由于边的权值是从后往前给的,在遍历第一条边的时候并不知道b[5]的值,所以一直到第五条边之前都不会更新,直到遍历第五条边,得到了b[2]开始得到暂时最短路,b[3]的暂时最短路可以从b[2]的暂时最短路推算出来。
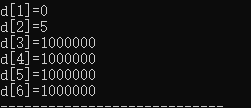
后面到n-1次的更新
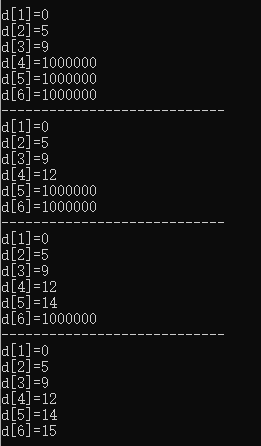
第n次应该不再更新,如果数据还有更新说明图有负权环
SPFA最短路算法
1.#include"bits/stdc++.h"
2.using namespace std;
3.const int INF=1e6;
4.const int NUM=105;
5.struct edge{//记录边的情况
6. int from,to,w;
7. edge(int a,int b,int c){from = a;to = b;w = c;}//构造函数
8.};
9.vector< edge > e[NUM];
10.int n,m;
11.int pre[NUM];//记录前驱节点,pre[x]=y,表示x的前一个节点是y
12.void print_path(int s,int t){}
13.int spfa(int s){
14. int dis[NUM];//记录所有节点到起点的距离
15. bool inq[NUM];//inq[i]==true表示该节点在队列中
16. int Neg[NUM];
17. memset(Neg,0,sizeof(Neg));
18. Neg[s]=1;
19. for(int i=1;i<=n;i++){dis[i]=INF;inq[i]=false;}
20. dis[s]=0;//起点到自己的距离是0
21. queue<int>Q;
22. Q.push(s);
23. inq[s]=true;
24. while(!Q.empty()){
25. int u=Q.front();
26. Q.pop();
27. inq[u]=false;
28. for(int i=0;i<e[u].size();i++){//检查节点u的所有邻居
29. int v=e[u][i].to,w=e[u][i].w;
30. if(dis[u]+w<dis[v]){//如果u的第i个邻居,通过u这个节点离s更近的话就更新
31. dis[v]=dis[u]+w;//更新它的暂时最距离
32. //pre[v]=u;//如此一来,v的前一个节点就是u了
33. if(!inq[v]){//u的第i个邻居状态更新了,但是不在队列中,就入队
34. inq[v]=false;
35. Q.push(v);
36. Neg[v]++;
37. if(Neg[v]>n)return 1;//如果该节点入队次数大于n了说明出现负圈
38. }
39. }
40. }
41. }
42. printf("%d\n",dis[n]);//n到s的最短距离
43. //print_path(s,n);//如有需要,打印最短路径
44. return 0;
45.}
46.int main(){
47. while(~scanf("%d %d",&n,&m)){
48. if(n==0&&m==0)return 0;
49. for(int i=1;i<=n;i++)e[i].clear();
50. while(m--){
51. int a,b,c;
52. scanf("%d %d %d",&a,&b,&c);
53. e[a].push_back(edge(a,b,c));
54. e[a].push_back(edge(b,a,c));
55. }
56. spfa(1);
57. }
58.}
Spfa算法是对bellman-ford算法的优化,bellman-ford算法每次循环都要更新所有节点到s的最短距离,有很多节点的值其实并没有变化,这其中产生了很多无效操作。而spfa算法只遍历访问当前节点的邻居,看看经过当前节点后邻居节点到s的最短距离有没有变化,如果有变换就更新那个邻居节点的值即可,一般使用队列来模拟这个过程,操作更针对化,高效。但是spfa算法是不稳定的,对于不同的图,队列的规模会有很大的差别。Spfa算法中,只要一个节点进入节点的次数大于所有节点的个数,就能判断出图中有负环
Dijkstra最短路算法
Dijstra是最稳定最高效的最短路算法,但是它不能判断图中是否有负环
1.struct edge{
2. int from,to,w;
3. edge(int a,int b,int c){from =a;to=b;w=c;}
4.};
5.vector<edge>e[NUM];//NUM==105
6.struct s_node{
7. int id,n_dis;//id是节点编号,n_dis是这个节点到s的距离
8. s_node(int b,int c){id=b;n_dis=c;}
9. bool operator < (const s_node & a)const {return n_dis>a.n_dis;}
10.};
11.void dijstra_path(){
12. int s=1;
13. int dis[NUM];//记录所有点到s的最短距离
14. bool done[NUM];//记录是否得到改点的最短距离
15. for(int i=1;i<=n;i++){dis[i]=INF;done[i]=false;}//INF=1e6
16. dis[s]=0;//s到自己的距离是0
17. priority_queue<s_node>Q;//因为距s距离最短的节点要出列,所以使用stl的优先队列
18. Q.push(s_node(s,dis[s]));
19. while(!Q.empty()){
20. s_nod u=Q.top();//把距s距离最短的节点出列
21. Q.pop();
22. if(done[u.id])continue;//如果已经找到该点的最短距离就直接跳过
23. done[u.id]=true;
24. for(int i=0;i<e[u.id].size();i++){
25. edge y=e.[u.id][i];
26. if(done[y.to])continue;//如果已经找到该点的最短距离就直接跳过
27. if(dis[y.to]>y.w+u.n_dis){//如果经过该点比直接连接s的距离更近,就更新距离
28. dis[to]=y.w+u.n_dis;
29. Q.push(s_node(y.to,dis[y.to])); //扩展新的邻居
30. }
31. }
32. }
33. printf("%d\n",dis[n]);
34.}
Dijstra最短路算法要使用优先队列和一个结构数组。
(1)由于起点s到它自己的距离是0,所以把起点s标记为已找到最短距离,然后先把s的所有邻居的距s的距离都放入优先队列内。此时队首元素x就是距离起点s最近的邻居节点。
(2)Pop队首元素x,然后把x的所有邻居的距s的距离都放入优先队列,x所有邻居距离s的距离就是x到s的距离+邻居节点距x的距离
(3)每次出队列的元素都标记以找到最短路径,就像一个源点的多米诺骨牌,骨牌倒的速度都一样,当骨牌到达某一节点时,此节点必是当前距s距离的最短节点,所以dijkstra最短路径算法每次都能确定一个节点的距s的最短距离,所以这算法是稳定的,是最高效的最短路径算法
