逐点比较法直线插补
原文:https://blog.csdn.net/qq_36552550/article/details/79356398
首先我们看看什么是直线插补?数控机床上的横向伺服电机(X轴)带动刀具在X轴向上进行移动,纵向伺服电机(Y轴)带动刀具在Y轴上进行移动,通过两个电机的协调运行将刀具的运动轨迹范围涵盖到整个二维平面上。所以,刀具从A点到B点移动,实际上并非是一条直线,而是通过X轴与Y轴方向的一步一步的运动来逼近理想下的AB直线。
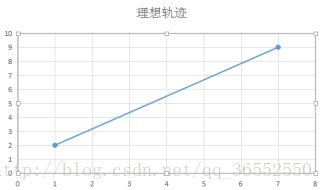
例如刀具想从点(1,2)移动至(8,9)点,理想状态下的轨迹如图5.1所示
图5-1 刀具从点(1,2)移动至(8,9)点的理想轨迹
但实际上横向伺服电机(X轴)与纵向伺服电机(Y轴)只能管控刀具在X轴与Y轴的移动,也就是说真实的刀具移动是不能如上图一般走斜线的。所以现实中的刀具运动轨迹如同图5.2所示。
图5-2 刀具从点(1,2)移动至(8,9)点的真实轨迹
如何对理想直线进行逼近,生成如图5.2中的数据点群,就是直线插补的功能所在。当我们给定的数据点群越密集,所生成的轨迹将越逼近与理想轨迹。那么计算机又是如何对根据给定的起始点以及终点进行过程点的计算给出呢?
通过该部分的学习,我们不仅能够掌握直线插补算法的程序编写,并且对C/C++程序语言基础的掌握程度有一个检验与加强。
5.1 逐点比较法直线插补原理
在二维坐标系下,给定起点(xs,ys)和终点(xe,ye),计算机是如何计算出所有图1.2所示的过程点呢,或者说如何走出图1.2的路线呢?这就是本节的内容——逐点比较法直线插补原理。该方法通俗来讲就是过给定的起点和终点连线,当过程点(xi,yi)在连线下面的时候(过程点是变化点,表示路径信息),往上走一步;当过程点(xi,yi)在连线上面的时候,向下走一步(为了方便,正好处于连线上时可以归纳至任意一种情况)。
计算机与人不同,它只能通过计算来判别一点处于一条直线的上面还是下面,这里就要用到我们初中的几何知识——直线斜率的计算。将给定起点(xs,ys)和终点(xe,ye)的进行连线,其斜率为k1,我们能够得出;然后我们将起点(xs,ys)与当前过程点(xi,yi)进行连线并求解其斜率k2,得出,比对两者大小我们就能够得出下一步如何走,即确定下一个过程点。当然,这种比对是在一个判定好的大前提条件下进行的,我们看看这些前提条件的分类和判定。
在计算机运行过程中,我们需要考虑到所有情况,否则将容易出现意外的错误,也就是人们口中常说BUG。这里我们将情况分为6类:第一象限走向、第二象限走向、第三象限走向、第四象限走向、X轴正负方向走向、Y轴正负方向走向。
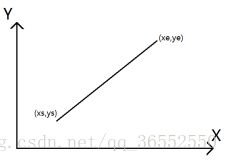
A)第一象限走向:
当xe>xs且ye>ys时,走向为第一象限走向,如图5-3所示。我们从初中几何知识可知,当k2大于k1的时候,即(xe-xs)(yi-ys)-(xi-xs)(ye-ys)>0,过程点位于线上方,此时将沿X轴正方向行走一步,即xi+1;当k2小于k1的时候,即(xe-xs)(yi-ys)-(xi-xs)(ye-ys)<0,过程点位于线下方,此时将沿Y轴正方向行走一步,即yi+1。
图5-3 第一象限走向示意图
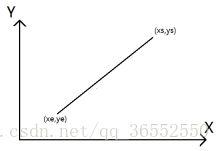
B)第二象限走向:
当xe
图5-4 第二象限走向示意图
C)第三象限走向:
当xe
图5-5 第三象限走向示意图
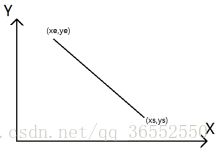
D)第四象限走向:
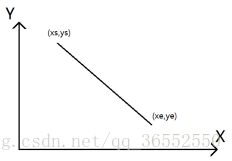
当xe>xs且ye
图5-6 第四象限走向示意图
E)X轴正负方向走向
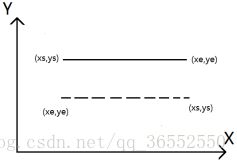
如图5-7所示,当ys=ye且xs
图5-7 X轴正负方向走向示意图
F)Y轴正负方向走向
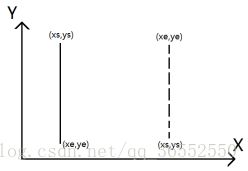
如图5-8所示,当xs=xe且ys
图5-8 Y轴正负方向走向示意图
此外,我们需要对行进有一个限制,也就是说当过程点放在起始位置开始向终点行进时,到达终点后,我们应该停止。很容易得出,行进的次数,然后通过一个for语句或者while语句即可实现插补次数的限制。大家可以根据以上原理,联系前面所学内容自己试着写一写,然后参考下一节的内容进行修改和比对。
5.2 逐点比较法直线插补程序实现
上一节我们将走向分了四类,以第一象限走向为例,其中判定条件为xe>xs且ye>ys,这里面有两个子条件——xe>xs、ye>ys,并且需要同时满足才能够认为该条件为真。这在程序里面如何进行实现的呢?逻辑运算。
5.2.2 程序实现
该程序实现通过输入流cin来输入两个坐标——起点与终点,然后输出对应的插补过程点。程序如表5-3所示。
#include
#include
using namespace std;
int main()
{
int Nxy,xs,ys,xe,ye,xi,yi,XieLvChaZhi;
//Nxy为插补总次数,xs与ys为起点坐标,xe与ye为终点坐标,xi与yi为插补过程点,XieLvChaZhi为斜率差值。
cout<<"请输入起点坐标:"<>xs>>ys;
cout<<"请输入终点坐标:"<>xe>>ye;
Nxy =abs((xe-xs))+abs((ye-ys));
xi=xs;
yi=ys;
//以上两行代码实现将过程点放在起点坐标上面。
for(int i=0;i0)
{
yi++;
}
else
{
yi--;
}
cout<0)
{
xi++;
}
else
{
xi--;
}
cout<0)&&(ye-ys>0))
{
if (XieLvChaZhi>=0)
{
xi++;
}
else
{
yi++;
}
cout<0))
{
if (XieLvChaZhi<=0)
{
xi--;
}
else
{
yi++;
}
cout<0)&&(ye-ys<0))
{
if (XieLvChaZhi>=0)
{
yi--;
}
else
{
xi++;
}
cout< 表5-3 逐点比较法直线插补程序
整个程序通过输入输出流实现了起点与终点坐标的输入;计算得出插补的总次数Nxy的大小,以便我们通过for循环语句来实现插补次数的控制;在for循环语句中枚举出我们前面所提到的六种情况。当然,该程序中的for循环语句可以用while语句来替代,大家可以使用while语句实现一下,以检验自己前面所学的知识。