三步学通哈夫曼树

前言

哈夫曼树的历史由来。
1951年，哈夫曼在麻省理工学院（MIT）攻读博士学位，他和修读信息论课程的同学得选择是完成学期报告还是期末考试。导师罗伯特•法诺（Robert Fano）出的学期报告题目是：查找最有效的二进制编码。由于无法证明哪个已有编码是最有效的，哈夫曼放弃对已有编码的研究，转向新的探索，最终发现了基于有序频率二叉树编码的想法，并很快证明了这个方法是最有效的。哈夫曼使用自底向上的方法构建二叉树，避免了次优算法香农-范诺编码（Shannon–Fano coding）的最大弊端──自顶向下构建树。
1952年，于论文《一种构建极小多余编码的方法》（A Method for the Construction of Minimum-Redundancy Codes）中发表了这个编码方法。
哈夫曼（Huffman）树,又称最优二叉树，是一种带权路径长度最短的二叉树，它在信息传输、数据压缩、优化算法等方面都有应用。

正文

第一步：先要明确以下几个概念：

哈夫曼树，是树的一种，所以学习哈夫曼树，先要把树的概念要学懂，所以要学会下面树的定义及树的基本术语：

●树的定义：树是由n(n>=0)个结点组成的有限集。若n=0，则该树为空树；若n>0,则树满足：①有且仅有一个特定的称为根（Root）的结点；②若除根以外还有其它结点，则其它结点可以划分为m(m>=1)个互不相交的有限集T1,T2,…,Tm,其中每一个集合本身又是一棵树，称为根的子树。

●树的基本术语：
①树的结点：树的结点包含一个数据元素及若干指向其子树的分支。例如，图（一）中的从A到O都是结点。
②结点的度：结点拥有的子树数量（一个结点含有的子结点的个数称为该结点的度）。例如，图（一）中结点B有三棵子树，它的度为3。
③叶子：度为0的结点称为叶子或终端结点。例如，图（一）中的F,G,I,J,K,L,M,N和O是叶子。
④分支结点：度不为0的结点称为分支结点或非终端结点。例如，图（一）中的A,B,C,D,E,H是分支结点。
⑤树的度：树内各结点度的最大值。例如，图（一）中的树的度为3。
⑥孩子（儿子）结点：该结点子树的根。例如，图（一）中结点B有三棵子树，（E（L，M））、（F）、（G），三棵子树的根分别为Ｅ、Ｆ和Ｇ。
⑦双亲（父亲）结点：若B是A的孩子结点，则称Ａ是B的父结点。
⑧兄弟结点：同一个双亲的孩子结点称为兄弟结点。
⑨堂兄弟结点：双亲在同一层的结点互为堂兄弟。例如，图（一）中G、H、I是堂兄弟，M、N也是堂兄弟。
⑩祖先结点：从根结点到该结点所经分支上的任何结点，称为该结点的祖先结点。例如，图（一）中的A,C和H是结点N的祖先结点。
○11子孙结点：以某结点为根的子树上的任何结点都是该结点的子孙结点。例如，图（一）中的E,L,M,F和G是结点B的子孙结点。
○12结点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推。
○13树的高度或深度：树中结点的最大层次。例如，图（一）中，树的深度为4。
○14路径和路径长度：在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1。例如，图（一）中，A到N的路径长度为3。
○15结点的权及带权路径长度：若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积。
○16树的带权路径长度：树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL。
○17森林：由m（m>=0）棵互不相交的树的集合称为森林。
●二叉树：每个结点最多含有两个子树的树称为二叉树。
●定理：对于具有n个叶子结点的哈夫曼树,共有2n-1个结点。

第二步：哈夫曼树介绍

1哈夫曼树的定义
哈夫曼（Huffman）树,又称最优二叉树，是一种带权路径长度最短的二叉树。给定n个数值{ W1,W2,…,Wn}，若将它们作为n个结点的权，并以这n个结点为叶子结点构造一颗二叉树，那么就可以构造出多棵具有不同形态的二叉树，其中带权路径长度最短的那棵二叉树称为哈夫曼树，或称最优二叉树。如图（二）所示：

2 构建哈夫曼树的方法

哈夫曼最早给出了一个带有一般规律的算法,成为哈夫曼算法。哈夫曼算法如下:
(1):根据给定的n个权值{W1,W2,….,Wn}构造n棵二叉树的森林T{T1,T2,…Tn}，其中每棵二叉树Ti (1≤i≤n)中都只有一个带权Wi为的根结点，其左、右子树均为空。
(2):在森林T中选取两棵结点权值最小的子树分别作为左、右子树构造一棵新的二叉树、且使左子树的权值小于右子树的权值、且置新的二叉树的根结点的权值为其左、右子树上根结点的权值之和。
(3):在森林T中，删除这二棵树，同时将新得到的二叉树加入Ｔ中。
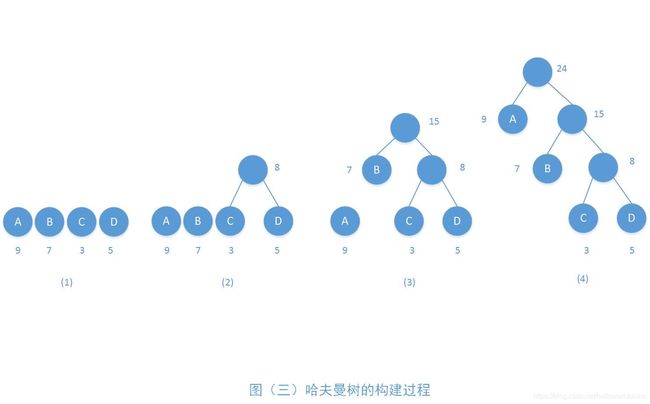
(４):重复(2)与(3)，直到T只含一棵树为止，这棵树便是哈夫曼树。如图（三）所示：

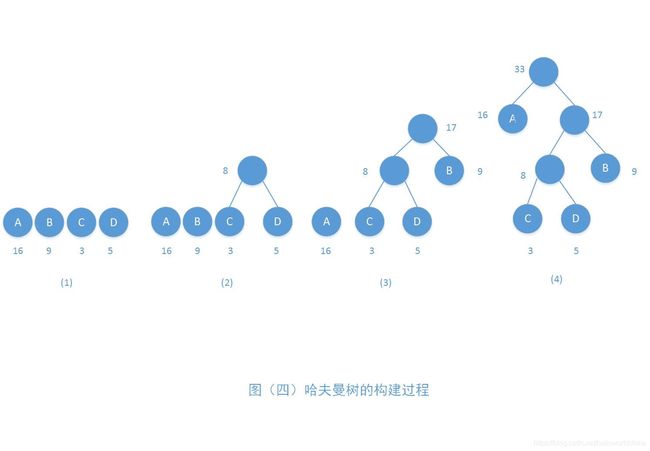
因为权值的不同，哈夫曼树的样子有点不同，为了加深对哈夫曼树构建过程的认识，笔者再列举一个哈夫曼树的构建，见图（四）：

第三步：代码实现

1 C++代码
详见《哈夫曼树之C++实现》（https://blog.csdn.net/helloworldchina/article/details/105210853）。

2 C#代码
详见《哈夫曼树之C#实现
》(https://blog.csdn.net/helloworldchina/article/details/105691361)

3 java代码

import java.util.Scanner;

public class HuffmanTree {
    static boolean pr=false;//true  打印测试日志
    //哈夫曼树的结构
    static  class HTNode{
        int weight;    // 权值
        int parent, lChild, rChild;    // 双亲及左右孩子的下标
        HTNode(){
            //自定义的构造函数,为申请内存空间
        }
    }

    //输出哈夫曼树各结点信息
    static void print(HTNode[] hT) {
        System.out.println("index weight parent lChild rChild");
        String str="";
        for(int i = 1, m = hT[0].weight; i <= m; i++){

            str=String.format("%-8d", i);
            System.out.print(str);

            str = String.format("%-8d", hT[i].weight);
            System.out.print(str);

            str = String.format("%-8d", hT[i].parent);
            System.out.print(str);

            str = String.format("%-8d", hT[i].lChild);
            System.out.print(str);

            str = String.format("%-8d", hT[i].rChild);
            System.out.print(str);

            System.out.println();

        }
    }
    // 选择权值最小的两颗树
    static int[] selectMin(HTNode[]  hT, int k, int index1, int index2) {
        index1 = index2 = 0;
        int[] resultInt=new int[2];
        int i,j;
        for(j = 1; j <= k;j++){//使index1,index2分别指向hT中最前面的两个无双亲的结点
            if(0 == hT[j].parent) {
                if( 0== index1) {
                    index1 = j;
                }
                else {
                    index2 = j;
                    break;
                }
            }
        }

        if(hT[index1].weight > hT[index2].weight) {//使结点index1的权小于index2的权
            int t = index1;
            index1 = index2;
            index2 = t;
        }

        for(i =j+1; i<k;  i++){//继续查找没有双亲且权值最小的两个结点，将其地址记在index1和index2中
            if(0 == hT[i].parent) {
                if(hT[i].weight < hT[index1].weight) {
                    index2 = index1;
                    index1 = i;
                }else if(hT[i].weight < hT[index2].weight) {
                    index2 = i;
                }
            }
        }
        resultInt[0]=index1;
        resultInt[1]=index2;
        return resultInt;
    }
    // 构造有n个权值（叶子结点）的哈夫曼树
    static boolean createHufmanTree(HTNode[] hT,int n,int k)
    {
        if (n<=1) return false;
        //给数组赋初值0
        for(int i = 0; i <= k; i++){
            hT[i]=new HTNode();// 如不使用此行代码，执行到hT[i].parent =0时会报空指针异常
            hT[i].parent =0;
            hT[i].lChild =0;
            hT[i].rChild =0;
        }
        System.out.println("请依次输入权值，并回车确认");
        for(int i = 1; i <= n; i++){
            Scanner inputW = new Scanner(System.in);
            hT[i].weight=inputW.nextInt();    // 输入权值
        }
        hT[0].weight = k;    // 用0号结点保存结点数量

        if (pr)
        {
            System.out.println( "打印初始的数组:");
            print(hT);
        }

        /****** 初始化完毕, 创建哈夫曼树 ******/
        for(int i = n + 1; i <=k; i++)
        {
            int index1=-1, index2=-1;
            int[] resultInt=new int[2];
            resultInt=selectMin(hT, i, index1, index2);
            index1=resultInt[0];
            index2=resultInt[1];
            hT[index1].parent = hT[index2].parent = i;
            hT[i].lChild = index1; hT[i].rChild = index2;    // 作为新结点的孩子
            hT[i].weight = hT[index1].weight + hT[index2].weight;    // 新结点为左右孩子结点权值之和

            if (pr)
            {
                System.out.println("打印构建哈夫曼树过程中的数组:");
                System.out.println("i=" +i);
                System.out.println("index1=" +index1+";index2="+index2);
                print(hT);
            }
        }
        return true;
    }
    static int huffmanTreeWPL_w(HTNode[]  hT, int i, int deepth)
    {
        if(hT[i].lChild == 0 && hT[i].rChild == 0)
        {
            return hT[i].weight * deepth;
        }
        else
        {
            return huffmanTreeWPL_w(hT, hT[i].lChild, deepth + 1) + huffmanTreeWPL_w(hT, hT[i].rChild, deepth + 1);
        }
    }
    // 计算WPL（带权路径长度）
    static int huffmanTreeWPL(HTNode[] hT)
    {
        return huffmanTreeWPL_w(hT, hT[0].weight, 0);
    }

    public static void main(String[] args){
        System.out.println("请输入权值的数量n=? ");
        int n, k;//n 权值数（叶子结点数）  k结点的个数
        Scanner input = new Scanner(System.in);
        n = input.nextInt();
        k = 2*n - 1;
        //创建存储哈夫曼树的数组
        HTNode[] hT=new HTNode[k+1];// 0号结点不使用
        if (createHufmanTree(hT,n,k))
        {
            System.out.println("打印哈夫曼树数组:");
            print(hT);
            System.out.println("WPL = " +huffmanTreeWPL(hT));
        } else System.out.println("输入有误，不能创建哈夫曼树!");

    }
}

4运行结果