曲线坐标系与直角坐标系转换(一)——基础:matlab插值函数简介
一、概念与应用
1、概念
插值法又称“内插法”,是利用函数f (x)在某区间中已知的若干点的函数值,作出适当的特定函数,在区间的其他点上用这特定函数的值作为函数f (x)的近似值,这种方法称为插值法。如果这特定函数是多项式,就称它为插值多项式(百度百科)
插值法作用——有效预测未知点
从已知点近似计算未知点的近似计算方法,即构造一个多项式函数,使其通过所有已知点,然后用求得的函数预测位置点。
讲解matlab中插值函数的
2、应用
常常需要根据已知的函数点进行数据、模型的处理和分析,而通常情况下现有的数据是极少的,不足以支撑分析的进行,这时就需要使用一些数学的方法,“模拟产生”一些新的但又比较靠谱的值来满足需求。
二、matlab插值函数
MATLAB中的插值函数为interp1,
语法: yi= interp1(x,y,xi,'method')
其中x,y为插值点,yi为在被插值点xi处的插值结果;x,y为向量, 'method'表示采用的插值方法,MATLAB提供的插值方法有几种: 'method'是最邻近插值, 'linear'线性插值; 'spline'三次样条插值; 'cubic'三次插值.缺省时表示线性插值
【注意:所有的插值方法都要求x是单调的,并且xi不能够超过x的范围,对于非单调x,采用x,y分别构造关于t的参数方程】
【注意:所有的插值方法都要求x是单调的,并且xi不能够超过x的范围,对于非单调x,采用x,y分别构造关于t的参数方程】
【注意:所有的插值方法都要求x是单调的,并且xi不能够超过x的范围,对于非单调x,采用x,y分别构造关于t的参数方程】
(重要事情说3遍)
例如:在一 天24小时内,从零点开始每间隔2小时测得的环境温度数据分别为
12,9,9,10,18 ,24,28,27,25,20,18,15,13,
推测中午12点(即13点)时的温度.
x=0:2:24;
y=[12 9 9 10 18 24 28 27 25 20 18 15 13];
a=13;
y1=interp1(x,y,a,'spline')
结果为: 27.8725
若要得到一天24小时的温度曲线,则:
xi=0:1/3600:24;
yi=interp1(x,y,xi, 'spline');
plot(x,y,'o' ,xi,yi)
![]()
命令1 interp1
功能 一维数据插值(表格查找)。该命令对数据点之间计算内插值。它找出一元函数f(x)在中间点的数值。其中函数f(x)由所给数据决定。
x:原始数据点
Y:原始数据点
xi:插值点
Yi:插值点
格式
(1)yi = interp1(x,Y,xi)
返回插值向量yi,每一元素对应于参量xi,同时由向量x 与Y 的内插值决定。参量x 指定数据Y 的点。
若Y 为一矩阵,则按Y 的每列计算。yi 是阶数为length(xi)*size(Y,2)的输出矩阵。
(2)yi = interp1(Y,xi)
假定x=1:N,其中N 为向量Y 的长度,或者为矩阵Y 的行数。
(3)yi = interp1(x,Y,xi,method)
用指定的算法计算插值:
’nearest’:最近邻点插值,直接完成计算;
’linear’:线性插值(缺省方式),直接完成计算;
’spline’:三次样条函数插值。对于该方法,命令interp1 调用函数spline、ppval、mkpp、umkpp。这些命令生成一系列用于分段多项式操作的函数。命令spline 用它们执行三次样条函数插值;
’pchip’:分段三次Hermite 插值。对于该方法,命令interp1 调用函数pchip,用于对向量x 与y 执行分段三次内插值。该方法保留单调性与数据的外形;
’cubic’:与’pchip’操作相同;
’v5cubic’:在MATLAB 5.0 中的三次插值。
-------------------------------------------详解-----------------------------------------
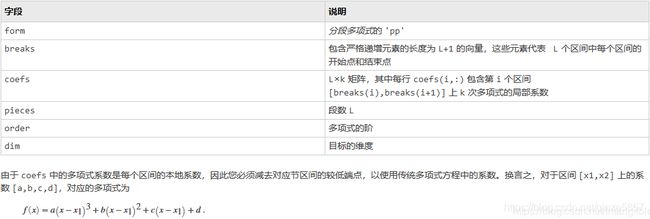
一、pchip全称(piecewise cubic hermite interpolation polynomial)分段三次艾米特插值多项式
infomation : matlab 指令 help pchip
语法:
yi = pchip(x,y,xi)——返回与 xi中的查询点对应的插值 p 的向量。p 的值由 x 和 y 的保形分段三次插值确定。
输入参数:
x,y为采样点,维度相同,xi为内插点,是 pchip 计算出的插值函数值 p 的 x 坐标
返回:yi为xi对应的输出点
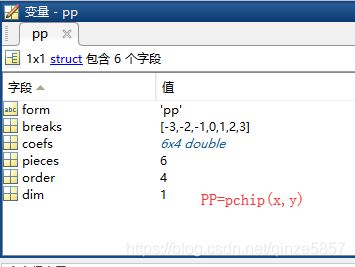
pp = pchip(x,y)——返回一个分段多项式结构体以用于 ppval 和样条实用工具 unmkpp
输入参数:
x,y为采样点,维度相同
返回:pp结构体
以下是help pchip信息
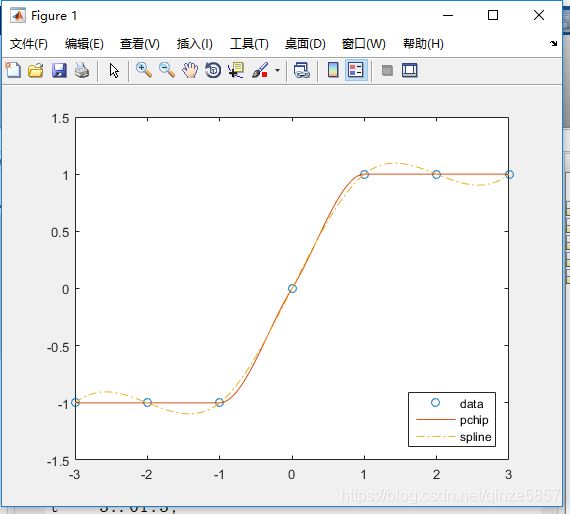
example
x = -3:3;
y = [-1 -1 -1 0 1 1 1];
t = -3:.01:3;
p = pchip(x,y,t);
s = spline(x,y,t);
plot(x,y,'o',t,p,'-',t,s,'-.')
legend('data','pchip','spline','Location','SouthEast')pchip与spline的区别:
- 样条插值曲线产生光滑的结果,如二阶导连续
- 样条插值曲线产生更精确的结果,如果数据包含光滑函数的值
- pchip没有超调量,如果数据不光滑,更少的震荡
- pchip建立起来更少代价
- 两种方法评估代价相等
源解释:
,