一些常用算法以及思想（待更新）

排序算法

1.快速排序（Quick Sort）

快速排序本质是在一个序列中先确定一个标准值，然后将比标准值大的数放在标准值右侧，比标准值小的数放在标准值左侧。
接着递归的在左侧和右侧继续执行此操作，最终我们就能够得到正常的序列。

实现方法：
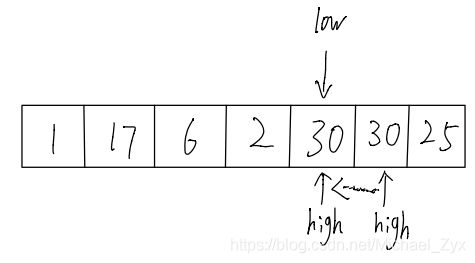
1. ⾸先确定⼀个标准值，这⾥假定序列第⼀个值就是标准值，设⽴两个指针，指向序列的头和尾

2. 先从后往前扫描，在high指针所指的位置发现⽐标准值⼩或者相等的数就⽤这个值覆盖掉low所指位置存储的值，接着low指针向右移动，否则high指针继续向左移动，直到找到⼩于或者等于标准值的数。

3. 之后从前往后扫描，直到找到第⼀个⼤于标准值的数，⽤它替换掉high指针所指位置的值，之后high向左移动，同理，如果之前没有找到⼤于标准值的数，low指针⼀直向右移动。

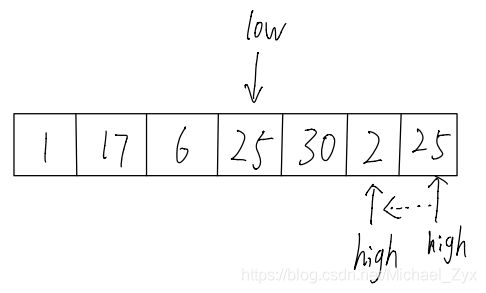
4. 接着重复步骤2，保证从前往后扫描，从后往前扫描是交替进行的。

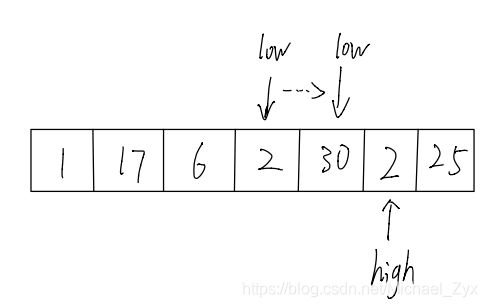
5. 当low指针和high指针相等时，我们就可以把标准值填⼊，相当于我们通过这种⽅式找到了标准值应该处在的正确索引位置，可以发现，此刻标准值左侧都是⽐它⼩的数，右侧都是⽐它⼤的数。

为何这样可行呢？因为每次我们都将比标准值大的数抛向右边，并且将比标准值小的数抛向左侧。
为什么扫描方向要交替进行呢？因为每次扫描相当于是找到了某个数应该存在的位置，并且把它抛了过去，但是原本的位置我们并不知道要填入什么数，它处于一个未知状态，因此我们要通过交换扫描顺序将原本未知的地方进行填补。

实现代码（java）：

public class QuickSort {
    public void quicksort(int[] num,int low,int high){
        if (low<high){//跳出整个递归的条件
            int test = num[low];
            int low2 = low;
            int high2 = high;
            int choose = 1;
            while (low2<high2){//每次只干一件事,先从后往前扫描，然后从前往后扫描，之前没进行替换就换方向扫描了
                if(choose == 1){//信号量choose保证了扫描方向的交替进行
                    while(num[high2]>test && low2<high2 ){
                        high2--;     //没找到需要更改位置的数则继续移动指针
                    }
                    num[low2] = num[high2];
                    /*if (num[high2]<=test){
                        num[low2] = num[high2];
                        low2++;
                    }
                    else {
                        high2--;
                    }*/
                    choose--;
                }
                else {
                    while (num[low2]<=test && low2<high2){
                        low2++;    //没找到需要更改位置的数则继续移动指针
                    }
                    num[high2] = num[low2];
                    /*if (num[low2]>test){
                        num[high2] = num[low2];
                        high2--;
                    }
                    else {
                        low2++;
                    }*/
                    choose++;
                }
            }
            num[low2] = test;//找到标准值应处的正确位置，要把值赋进去
            quicksort(num,low,low2-1); //递归的进行运算，按相同方式处理前半部分与后半部分
            quicksort(num,low2+1,high);
        }
    }
}

2.归并排序（Merge Sort）

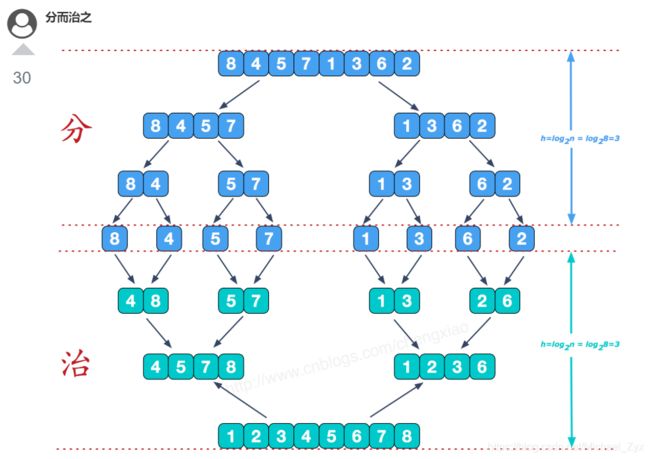
归并排序实际用到的是“分治算法”的思想，首先将一个序列从中间进行拆分，分成两个部分，再分别将这两个部分继续拆分，可以自定义拆分程度，也就是最小序列长度，这里我们定义把序列拆分到只有一个数（如果定义的最小长度序列不是单独的数，需要保证它已经按照要求用别的排序方法排好符合要求的序列）。
拆分完毕后，再进行合并，合并时需要保证两点:
1.被合并的序列已经是符合排序要求的序列
2.合并形成的新序列也是符合排序要求的序列

这里引用一张图：来自 https://www.runoob.com/w3cnote/merge-sort.html

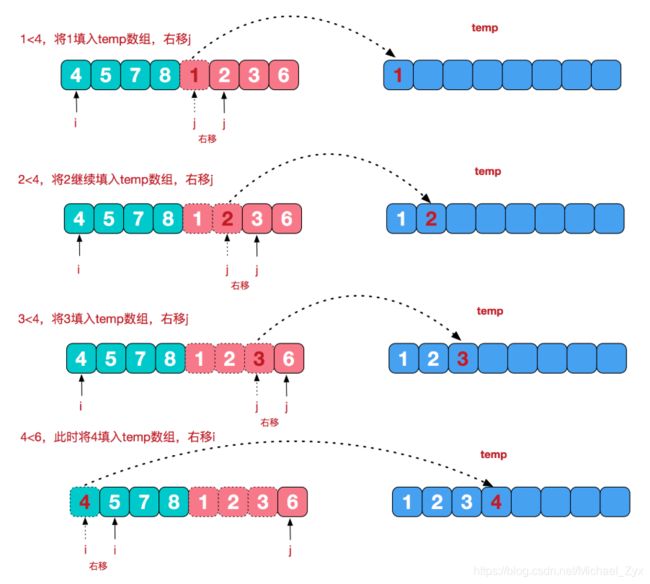
接下来的问题在于，我们如何将两个已经符合要求的序列，合成新的符合要求的序列，这里继续引用一张图：来自 来自 https://www.runoob.com/w3cnote/merge-sort.html

如图所示，绿色序列以及红色序列是已经符合排序要求的子序列，蓝色序列是我们要得到的合成序列


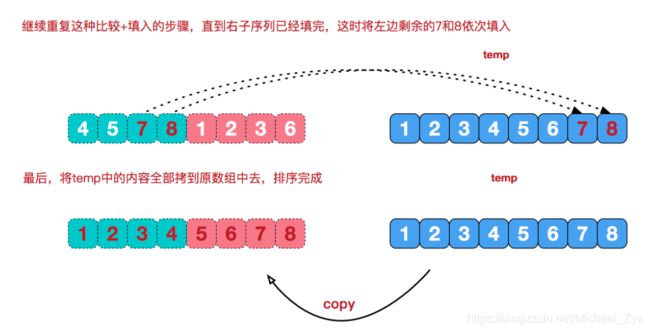
实现代码（java）：

public class MergeSort {
    public void merge(int[] f,int lb,int mid,int ub) {//归并的过程
        int a[]=new int[ub-lb+1];
        int i=lb,j=mid+1,k=0;
        for (;i < mid+1 && j<ub+1;k++) {//此处进行比较，每次都将较小的值填入新序列
            if (f[i]<=f[j]){
                a[k] = f[i];
                i++;
            }
            else {
                a[k] = f[j];
                j++;
            }
        }

        while (i<mid+1){//判断是否出现某一个子序列已经全部填入新序列，而还有一个序列依旧有值未填入
                        //这时只需按序将此序列中的值放入新序列即可，因为剩下的值已经是按序存在的了
            a[k] = f[i];
            i++;
            k++;
        }

        while (j<ub+1){//和上面同理
            a[k] = f[j];
            j++;
            k++;
        }
        System.arraycopy(a, 0, f, lb, a.length);//将排序好的值赋给输入序列f，输入序列f是初始需要排序的序列
    }

    public void mergeSort(int[] f,int lb,int ub) {//整个归并排序过程，包括“分”和“治”
        if(lb<ub) {//注意递归结束条件，此处定义为序列最小就是1个数
            int mid=(lb+ub)/2;//lb,ub分别指lower bound和upper bound
            mergeSort(f,lb,mid);//整个序列左半部分完成归并排序
            mergeSort(f,mid+1,ub);//整个序列右半部分完成归并排序
            merge(f,lb,mid,ub);//将左右部分合并出来最终结果
        }

    }
}

2.搜索算法

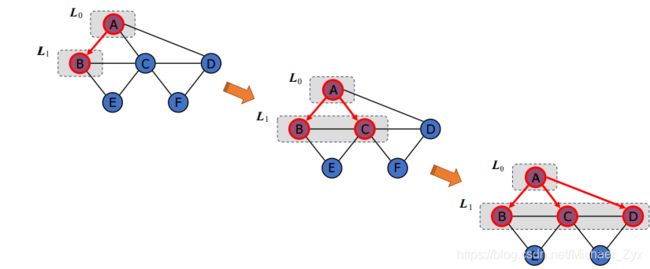
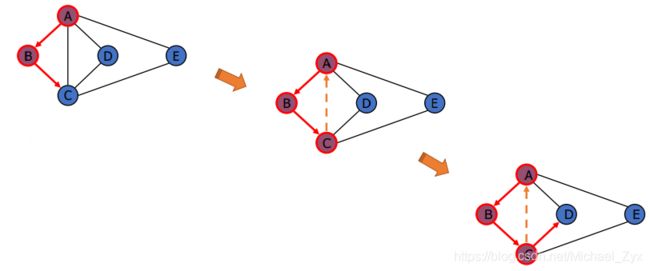
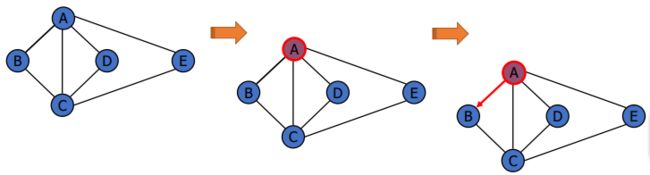
1.深度优先搜索

在图的遍历过程中经常使用。
基本思想是先选择一个起点，然后沿着一条可能的路径一直搜索，直到不可以继续前进，然后进行回溯，直到找到另外一条可以前进的路。

如图所示：图片来自作者:[email protected]

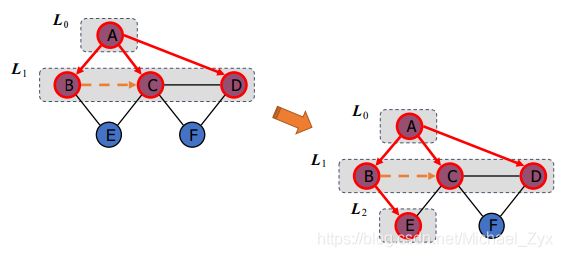
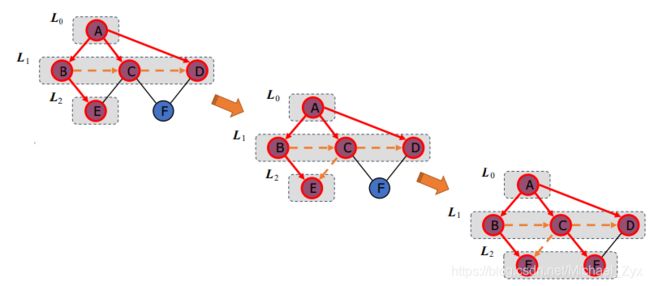
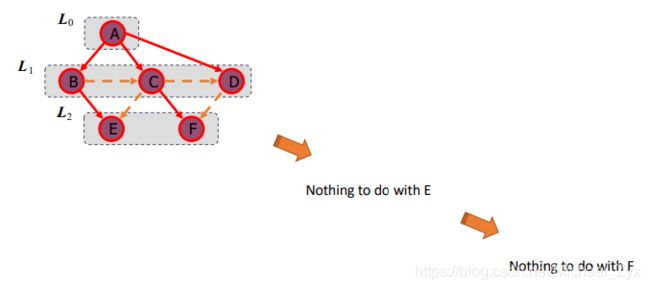
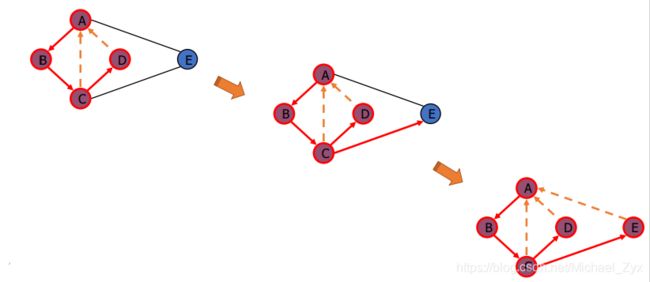
2.广度优先搜索

同样也是在图的遍历中经常使用。
基本思想是：选择一个起始点，然后探索当前深度下所有节点的邻居，之后再移动到下一个深度的节点继续按上面的规则探索。
如图所示：图片来自作者:[email protected]