零知识证明 - zkSNARK入门

网络上讲解零知识证明的文章就不多，这些文章要不太浅显，要不太深入，很少有能给入门者整体框架上的认识。

比如，阿里巴巴零知识证明就是一个非常好的通俗理解零知识证明的例子：

阿里巴巴被强盗抓住，为了保命，他需要向强盗证明自己拥有打开石门的密码，同时又不能把密码告诉强盗。他想出一个解决办法，先让强盗离开自己一箭之地，距离足够远让强盗无法听到口令，足够近让阿里巴巴无法在强盗的弓箭下逃生。阿里巴巴就在这个距离下向强盗展示了石门的打开和关闭。

这个整个过程就是零知识证明，证明者能够在不向验证者提供任何有用信息（石门的口令）的情况下，使验证者相信某个论断（阿里巴巴知道打开石门的方法）是正确的。

技术人除了通俗的理解零知识证明外，还需要对零知识的理论和推导过程深入理解运用。以太坊的一篇blog，比较适合想深入理解零知识证明的小伙伴。

https://blog.ethereum.org/2016/12/05/zksnarks-in-a-nutshell/

这篇文章也是这篇blog的翻译和我自己的理解。通过这篇文章，能快速建立零知识证明的逻辑框架。虽然这篇文章有些推导公式，但是相对简单，小伙伴可以耐心阅读。

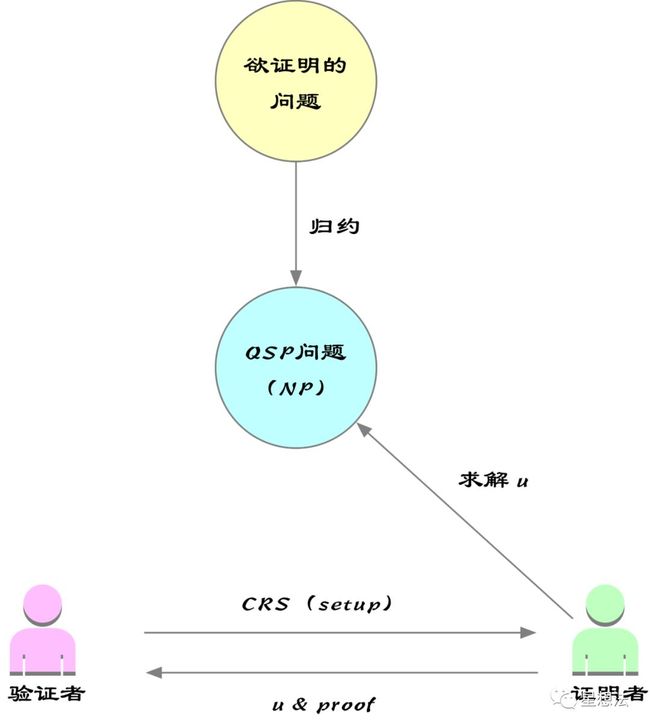
先给出零知识证明的逻辑框架：

0 - 零知识证明的基本概念

零知识证明，zkSNARK，zero-knowledge Succint Non-interactive ARguments of Knowledge的简称：

• Succinct：证明的数据量比较小
• Non-interactive：没有或者只有很少交互。
• ARguments：验证者只对计算能力有限的证明者有效。拥有足够计算能力的证明者可以伪造证明。这也叫“计算可靠性"（相对的还有”完美可靠性"）。
• of Knowledge：对于证明者来说在不知道证据（Witness，比如一个哈希函数的输入或者一个确定 Merkle-tree 节点的路径）的情况下，构造出一组参数和证明是不可能的。

零知识证明大体由四部分组成：

• 多项式问题的转化 - 需要证明的问题转化为多项式问题 t(x)h(x) = w(x)v(x)，证明者提交证明让验证者确认多项式成立。
• 随机挑选验证 - 随机选择验证的数值s，验证t(s)h(s) = w(s)v(s)。相对于验证多项式相等t(x)h(x) = w(x)v(x)，随机挑选验证，简单，验证数据少。随机挑选验证，安全性肯定不及多项式等式验证，但如果确实足够随机，安全性还是相当高的。
• 同态隐藏 - 同态隐藏指的是函数的一种特性。输入的计算和输出的计算保持“同态”。以加法同态为例，满足如下的三个条件的函数E(x)，称为加法同态：1. 给定 E(x)，很难推导出x. 2. 不同的输入，对应不同输出 3. E(x+y) 可以由 E(x)，E(y)计算出来。乘法同态类似。
• 零知识 - 证明者和验证者之间除了“问题证明与否”知识外，不知道其他任何知识（不知道随机挑选值，不知道挑选值的多项式计算结果等等）。

在了解零知识的基础概念上，慢慢推导整个零知识证明过程，先从NP问题说起。

1- NP问题以及约化

解决一个问题需要花费时间。如果解决问题需要的时间与问题的规模之间是多项式关系，则可以称该问题具有多项式复杂度。一般问题可分成两类：P问题和NP问题。P问题指的是在多项式时间内可解的问题。 NP问题（Non-Deterministic Polynomial Problem，非确定性多项式问题），指不能在多项式内可解，但是可以在多项式时间内验证的问题。

很显然，P问题也是NP问题，但是是否NP问题是P问题，NP=P？，目前为止还没有人能证明。一般认为，NP问题不等于P问题，也就是说，NP问题不存在多项式解法。

约化(Reduction)，可以理解成问题的转化。对任意一个程序A的输入，都能按某种法则变换成程序B的输入，使两程序的输出相同，那么，可以说，问题A可约化为问题B。

NPC问题，是一个NP问题，并且，其他所有的NP问题都能归约到它。简单的说，NP问题之间可以相互归约，一个NP问题求解，其他NP问题一样能求解。

举例说明，NP问题以及NP问题的归约。

布尔公式满足性问题（SAT问题，boolean formula satisfiability) 就是一个NP问题。布尔公式定义如下：

• 假设变量$x_1$, $x_2$, $x_3$, … 是布尔公式

• 假设f是布尔公式，$\neg f$也是布尔公式（取反）

• 假设f和g是布尔公式，$f\wedge g$和$f\vee g$也是布尔公式（与和或）

一个布尔公式可满足，指输入是0/1的情况下，存在输出为真。SAT问题指，找出所有可满足的布尔公式。SAT问题看上去，除了枚举一个个可能的布尔公式外，没有更好的办法，也就是多项式时间内不可解。如果知道一个可满足的布尔公式，验证非常方便（输入是0/1的情况下，看看输出是否为真）。SAT问题是NP问题。

再看看另外一个NP问题：PolyZero问题。PolyZero问题指某个多项式满足：多项式输入是0或1的情况下，多项式输出为0。

​ $$PolyZero(f):=1$$

f满足输入是0/1的情况下，多项式输出为0。

一个布尔表达式f可以通过如下的归约函数r，转化为多项式：

• $$r(x_i):=(1-x_i)$$
• $$r(\neg f):=(1-r(f))$$
• $$r(f\wedge g):=(1-(1-r(f))(1-r(g)))$$
• $$r(f\vee g):=r(f)r(g)$$

也就是说，一个SAT问题，通过归约函数r，可以归约为一个PolyZero问题：f是可满足的，当且仅当r(f)输出为0。

​ $$SAT(f)=PolyZero(r(f))$$

总结一下，NP问题是在多项式时间内无解，但是可以多项式时间验证的问题。NP问题可以相互归约。

2 - QSP问题

需要证明的问题，肯定是NP问题，如果是P问题，不存在问题解的”寻找“，也就不存在证明。简单的说，zkSNARK问题处理的都是NP问题。既然NP问题相互可以归约，首先需要确定一个NP问题，其他NP问题都可以归约到这个NP问题，再进行证明。也就是，证明了一个NP问题，就可以证明所有NP问题。

QSP问题是个NP问题，也特别适合zkSNARK。为啥特别适合，目前还不需要深究。有相关的论文论证：https://eprint.iacr.org/2012/215.pdf。

QSP问题是这样一个NP问题：给定一系列的多项式，以及给定一个目标多项式，找出多项式的组合能整除目标多项式。输入为$n$位的QSP问题定义如下：

• 给定多个多项式：$v_0,...,v_m,w_0,...,w_m$
• 目标多项式：$t$
• 映射函数：$f:\left\{(i,j)|1\le i\le n,j\in 0,1\right\}\to \left\{1,...m\right\}$

给定一个证据（Witness）u，满足如下条件，即可验证u是QSP问题的解：

• $$a_k,b_k=1如果k=f(i,u[i])$$

• $$a_k,b_k=0如果k=f(i,1-u[i])$$

• $$v_a{w}_b能整除t，其中v_a=v_0+a_1{v}_1+...+a_m{v}_m,w_b=w_0+b_1{w}_1+...+b_m{w}_m$$

对一个证据u，对每一位进行两次映射计算（$u[i]$以及$1-u[i]$），确定多项式之间的系数。因为针对证据u的每一位，计算两次，确定多项式之间的系数，如果$2n<m$，多项式的选择还是有很大的灵活性。

如果证明者知道QSP问题的解，需要提供证据（也就是u）。验证者在获知证据u的情况下，按照上述的规则恢复出多项式的系数，验证$v_a{v}_b$是否能整除$t$：$th=v_a{w}_b$。为了方便验证者验证，证明者可以同时提供$h$。在多项式维度比较大的情况下，多项式的乘法还是比较复杂的。

有个简单的想法，与其验证者验证整个多项式是否相等，不如随机挑选数值进行验证。假设验证者随机挑选验证数值s，验证者只需要验证$t(s)h(s)=v_a(s)w_b(s)$。

以上是基础知识，下面开始介绍zkSNARK的证明过程。在继续深入一个QSP问题证明细节之前，先看看一个多项式问题的证明过程。

3 - 多项式问题的证明过程

假设一个多项式$f(x)=a_0+a_{1}x+a_2{x}^2+...+a_{d-1}{x}^{d-1}+a_d{x}^d$。证明一个多项式，即给定一个输入$x$，提供$f(x)$的证明。

3.1 有线群论基础（椭圆曲线）

定一个有限群，生成元是$g$，阶为$n$，则该群包括如下的元素：$g^0,g^1,g^2,...,g^{n-1}$。通过有限群加密的方式很简单：$E(x):=g^x$。也就是说，得知$g^x$的情况下，不能反推出$x$。

3.2 选定随机数

验证者随机选择一个有限群中的元素，比如$s$。提供如下的计算结果（$s$的不同阶的加密结果）：

$$E(s^0),E(s^1),...,E(s^d)$$

在生成这些计算结果后，$s$就不需要了，可以忘记。

3.3 $E(f(s))$计算

举个例子，$f(x)=4+2x+4x^2$，$E(f(s))=E(s^0{)}^{4}E(s^1{)}^{2}E(s^2{)}^4$。显然，$E(f(s))$ 可以不知道$s$ 的情况下，通过验证者提供的数据计算出来。

3.4 $\alpha$对

注意的是，验证者是不知道待证明的多项式参数的，即使证明者提供了$E(f(s))$，验证者也无法验证。 $\alpha$对的方法可以让验证者确认证明者是通过多项式计算出结果。 在3.2的基础上，验证者还随机选择另外一个元素$\alpha$，并提供额外的计算结果：

$E(\alpha s^0),E(\alpha s^1),...,E(\alpha s^d)$

证明者需要提供$E(f(s))$和$E(\alpha f(s))$。

$$E(f(s))=E(s^0{)}^{4}E(s^1{)}^{2}E(s^2{)}^4$$

$$E(\alpha f(s))=E(\alpha s^0{)}^{4}E(\alpha s^1{)}^{2}E(\alpha s^2{)}^4$$

3.5 配对函数

配对函数$e$，满足如下定义：

$$e(g^x,g^y)=e(g,g{)}^{xy}$$

验证者验证$\alpha$对的方式很简单，检验如下的等式是否成立：

$$e(E(f(s)),g^{\alpha })=e(E(\alpha f(s)),g)$$

假设$A=e(E(f(s)),B=E(\alpha f(s))$推导过程如下：

$$e(A,g^{\alpha })=e(E(f(s)),g^{\alpha })=e(g^{f(s)},g^{\alpha })=e(g,g{)}^{\alpha f(s)}$$

$$e(B,g)=e(E(\alpha f(s)),g)=e(g^{\alpha f(s)},g)=e(g,g{)}^{\alpha f(s)}$$

到此为止，验证者提供$\alpha$对的情况下，证明者可以证明通过某个多项式计算出某个结果，验证者不知道具体的多项式的参数。

3.6 $\delta$ 偏移

更进一步，证明者采用$\delta$ 偏移，甚至不想让验证者知道$E(f(s))$。采用$\delta$ 偏移，证明者不再提供$A$和$B$，而是随机一个$\delta$参数，提供$A^{\prime }$和$B^{\prime }$。

$$A^{\prime }=E(\delta +f(s))=g^{\delta +f(s)}=g^{\delta }{g}^{f(s)}=E(\delta )E(f(s))=E(\delta )A$$

$$B^{\prime }=E(\alpha (\delta +f(s)))=E(\alpha \delta +\alpha f(s))=g^{\alpha \delta +\alpha f(s)}=E(\alpha {)}^{\delta }E(\alpha f(s))=E(\alpha {)}^{\delta }B$$

很显然，验证者从$A^{\prime }$无法推导出$E(f(s))$，但验证者一样能验证$\alpha$对的配对函数是否成立：

$$e(A^{\prime },g^{\alpha })=e(E(\delta +f(s)),g^{\alpha })=e(g^{\delta +f(s)},g^{\alpha })=e(g,g{)}^{\alpha (\delta +f(s))}$$

$$e(B,g)=e(E(\alpha (\delta +f(s)),g)=e(g^{\alpha (\delta +f(s))},g)=e(g,g{)}^{\alpha (\delta +f(s))}$$

多项式的整个证明过程如下图所示：

4 - QSP问题的skSNARK证明

skSNARK证明过程分为两部分：a) setup阶段 b）证明阶段。QSP问题就是给定一系列的多项式$v_0,...,v_m,w_0,...,w_m$以及目标多项式$t$，证明存在一个证据$u$。这些多项式中的最高阶为$d$。

4.1 setup和CRS

CRS - Common Reference String，也就是预先setup的公开信息。在选定$s$和$\alpha$的情况下，发布如下信息：

• $s$和$\alpha$的计算结果

  $$E(s^0),E(s^1),...,E(s^d)$$

  $E(\alpha s^0),E(\alpha s^1),...,E(\alpha s^d)$

• 多项式的$\alpha$对的计算结果
  $$E(t(s)),E(\alpha t(s))$$

  $$E(v_0(s)),...E(v_m(s)),E(\alpha v_0(s)),...,E(\alpha v_m(s))$$

  $$E(w_0(s)),...E(w_m(s)),E(\alpha w_0(s)),...,E(\alpha w_m(s))$$

• 多项式的${\beta }_v,{\beta }_w,\gamma$ 参数的计算结果

  $$E(\gamma ),E({\beta }_v\gamma ),E({\beta }_w\gamma )$$

  $$E({\beta }_v{v}_1(s)),...,E({\beta }_v{v}_m(s))$$

  $$E({\beta }_w{w}_1(s)),...,E({\beta }_w{w}_m(s))$$

  $$E({\beta }_{v}t(s)),E({\beta }_{w}t(s))$$

4.2 证明者提供证据

在QSP的映射函数中，如果$2n<m$，$1,...,m$中有些数字没有映射到。这些没有映射到的数字组成$I_{free}$，并定义（$k$为未映射到的数字）：

$$v_{free}(x)=\sum _k{a}_k{v}_k(x)$$

证明者需提供的证据如下

• $$V_{free}:=E(v_{free}(s)),W:=E(w(s)),H:=E(h(s)),$$

• $$V_{free}^{\prime }:=E(\alpha v_{free}(s)),W^{\prime }:=E(\alpha w(s)),H^{\prime }:=E(\alpha h(s)),$$

• $$Y:=E({\beta }_v{v}_{free}(s)+{\beta }_{w}w(s))$$

$V_{free}/V_{free}^{\prime },W/W^{\prime },H/H^{\prime }$是$\alpha$对，用以验证$v_{free},w,h$是否是多项式形式。$t$是已知，公开的，毋需验证。$Y$用来确保$v_{free}(s)$和$w(s)$的计算采用一致的参数。

4.3 验证者验证

在QSP的映射函数中，如果$2n<m$，$1,...,m$中所有映射到的数字作为组成系数组成的二项式定义为（和$v_{free}$互补）：

$$v_{in}(x)=\sum _k{a}_k{v}_k(x)$$

验证者需要验证如下的等式是否成立：

• $$e(V_{free}^{\prime },g)=e(V_{free},g^{\alpha }),e(W^{\prime },E(1))=e(W,E(\alpha )),e(H^{\prime },E(1))=e(H,E(\alpha ))$$

• $$e(E(\gamma ),Y)=e(E({\beta }_v\gamma ),V_{free})e(E({\beta }_w\gamma ),W)$$

• $$e(E(v_0(s))E(v_{in}(s))V_{free},E(w_0(s))W)=e(H,E(t(s)))$$

第一个（系列）等式验证$V_{free}/V_{free}^{\prime },W/W^{\prime },H/H^{\prime }$是否是$\alpha$对。

第二个等式验证$V_{free}$和$W$的计算采用一致的参数。因为$v_{free}$和w都是二项式，它们的和也同样是一个多项式，所以采用$\gamma$ 参数进行确认。证明过程如下：

$$e(E(\gamma ),Y)=e(E(\gamma ),E({\beta }_v{v}_{free}(s)+{\beta }_{w}w(s)))=e(g,g{)}^{\gamma ({\beta }_v{v}_{free}(s)+{\beta }_{w}w(s))}$$

$$e(E({\beta }_v\gamma ),V_{free})e(E({\beta }_w\gamma ),W)=e(E({\beta }_v\gamma ),E(v_{free}(s)))e(E({\beta }_w\gamma ),E(w(s)))=e(g,g{)}^{({\beta }_v\gamma )v_{free}(s)}e(g,g{)}^{({\beta }_w\gamma )w(s)}=e(g,g{)}^{\gamma ({\beta }_v{v}_{free}(s)+{\beta }_{w}w(s))}$$

第三个等式验证$v(s)w(s)=h(s)t(s)$，其中$v_0(s)+v_{in}(s)+v_{free}(s)=v(s)$。

简单的说，逻辑是确认$v,w,h$是多项式，并且$v,w$采用同样的参数，满足$v(s)w(s)=h(s)t(s)$。

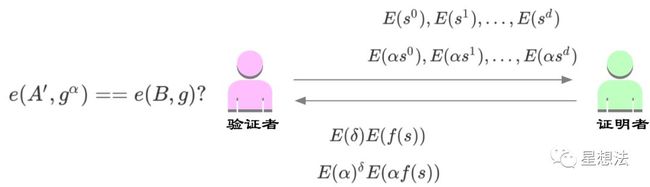
到目前为止，整个QSP的zkSNARK的证明过程逻辑已见雏形：

图2

4.4 $\delta$ 偏移

为了进一步“隐藏” $V_{free}$和$W$，额外需要采用两个偏移: ${\delta }_{free}和{\delta }_w$。 $v_{free}(s)/w(s)/h(s)$进行如下的变形，验证者用同样的逻辑验证。

$$v_{free}(s)\to v_{free}(s)+{\delta }_{free}t(s)$$
　$$w(s)\to w(s)+{\delta }_{w}t(s)$$
　$$h(s)\to h(s)+{\delta }_{free}(w_0(s)+w(s))+{\delta }_w(v_0(s)+v_{in}(s)+v_{free}(s))+({\delta }_{free}{\delta }_w)t(s)$$

至此，zkSNARK的推导逻辑就基本完整。使用zkSNARK证明，由如下的几步组成：

1/ 问题转化: 一个需要证明的NP问题转化为选定的NP问题（比如QSP问题）

2/ 设置参数（setup）：设置参数的过程也是挑选随机数的过程，并提供CRS

3/ 证明者获取证据u，通过CRS计算证据（proof）

4/ 验证者验证证据以及响应的proof

总结：零知识证明由四部分组成：多项式问题的转化，随机挑选验证，同态隐藏以及零知识。需要零知识证明的问题先转化为特定的NP问题，挑选随机数，设置参数，公布CRS。证明者，在求得证据的情况下，通过CRS计算出证据。验证者再无需其他知识的情况下可以进行验证。