数据结构与算法(二):查找+Low排序三人组(Python实现)
查找
列表查找
顺序查找
二分查找
排序
冒泡排序
选择排序
插入排序
一、查找
1、列表查找
从列表中查找指定元素
输入:列表、待查找元素
输出:元素下标或未查找到元素
li = [1,2,5,67,2,6,7]
# 第一种
6 in li
# 第二种
li.index(6)
2、顺序查找
从列表第一个元素开始,顺序进行搜索,直到找到为止。
for 循环实现,时间复杂度为O(n)。
3、二分查找
从有序列表的 候选区data[0:n] 开始,通过对待查找的值与候选区中间值的比较,可以使候选区减少一半。
传统办法:运用Python切片。
但是在列表很大的情况下,切片复制的数据量增加,导致效率低下。
所以,如果你会用C语言的指针,就会想到很好的解决办法:用变量来记录列表项位置。这会大大优化切片方法,提高运行效率。
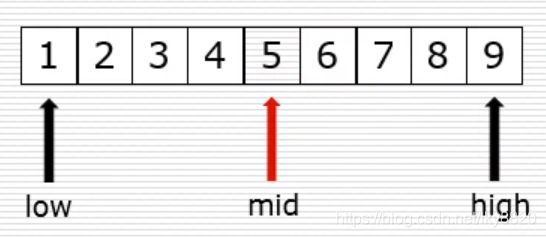
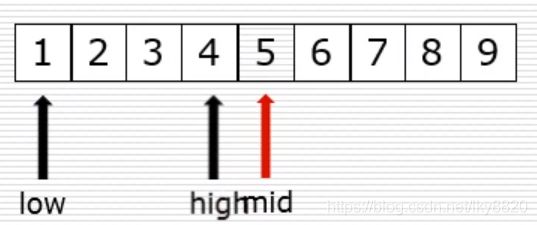
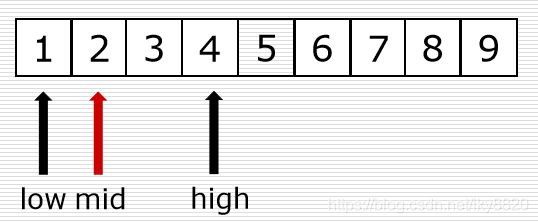
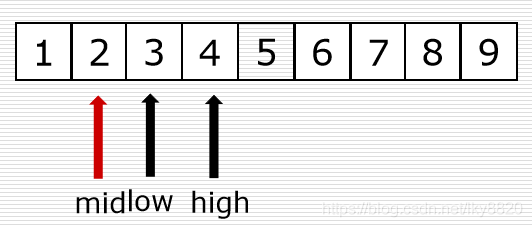
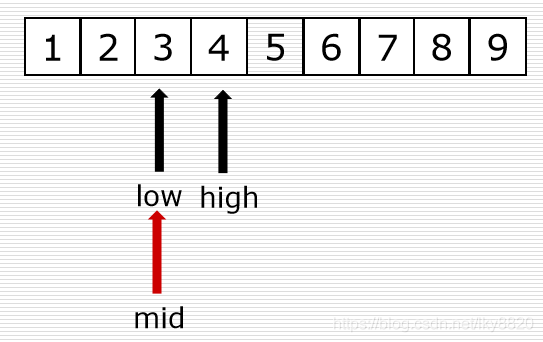
二分法代码实现:
# 二分查找
def bin_search(li, val):
low = 0
high = len(li) - 1
while low <= high: # 只要候选区不空,继续循环
mid = (low + high) // 2
if li[mid] == val:
return mid
elif li[mid] < val:
low = mid + 1
else: # li[mid] > val
high = mid - 1
return -1
上述代码时间复杂度:O( l o g 2 n log_2^n log2n)
可以与系统自带的查找方法,比较时间:
from cal_time import *
@cal_time
def sys_search(li, val):
try:
return li.index(val)
except:
return -1
li = list(range(0, 20000000, 2))
sys_search(li, 200000001)
index方法是一个一个查找的,而二分法是问题规模减半,时间复杂度O( l o g 2 n log_2^n log2n),速度很快。
系统方法不使用二分法做底层的原因是,无法一直保证列表是有序的,所以默认的查找方法都是顺序查找。
递归版本的二分查找代码实现:
def bin_search_rec(data_set, value, low, high):
if low <= high:
mid = (low + high) // 2
if data_set[mid] == value:
return mid
elif data_set[mid] > value:
return bin_search_rec(data_set, value, low, mid - 1)
else:
return bin_search_rec(data_set, value, mid + 1, high)
else:
return
在这里,笔者要提一嘴:
递归不一定会比循环运算速度低。
上述代码为尾递归(在结尾进行递归调用,没有跳出循环的环节),有一些编程语言会将尾递归进行优化,使之成为循环。
但是Python没有对尾递归进行优化,所以Python写递归结构依然比循环结构运行速度慢。
某些语言例如C++、Java都对尾递归进行了优化。
所以,能用循环写就不要使用递归方法。除了必须使用递归解决的问题,比如上一篇博文提到的汉诺塔问题,及接下来要提到的快速排序等等。
二、排序
1、冒泡排序
思路:列表每两个相邻的数,如果前边的比后边的大,那么交换这两个数。
代码实现:
from cal_time import *
# 冒泡排序
@cal_time
def bubble_sort(li):
for i in range(len(li) - 1): # i表示第n趟 一共n或者n-1趟
for j in range(len(li) - i - 1): # 第i趟 无序区[0, n-i-1] j表示箭头0~n-i-2,因为前包后不包,所以括号里仍然写n-i-1
if li[j] > li[j+1]:
li[j], li[j+1] = li[j+1], li[j]
li = list(range(10000))
random.shuffle(li)
bubble_sort(li)
print(li)
大概运行时间在10s左右。
大概时间估算:1s机器的运算量大概在 1 0 7 到 1 0 8 10^7到10^8 107到108左右。上述代码列表长度10000的平方是 1 0 8 10^8 108,计算 1 0 7 10^7 107次运算大概就是10s。
冒泡排序优化:
如果冒泡排序中执行一趟而没有交换,则列表已经是有序状态,可以直接结束算法。
优化代码如下:
def bubble_sort(li):
for i in range(len(li) - 1): # i表示第n趟 一共n或者n-1趟
exchange = False
for j in range(len(li) - i - 1): # 第i趟 无序区[0, n-i-1] j表示箭头0~n-i-2,因为前包后不包,所以括号里仍然写n-i-1
if li[j] > li[j+1]:
li[j], li[j+1] = li[j+1], li[j]
exchange = True
if not exchange:
break
最好情况:O(n) 完全有序
平均情况:O( n 2 n^2 n2)
最坏情况:O( n 2 n^2 n2)
稳定性:稳定(相邻的换位置,相等的不交换,所以稳定)
2、选择排序
思路:
一趟遍历记录最小的数,放到第一个位置。
再一趟遍历记录剩余列表中最小的数,继续放置。
…
问题:怎样选出最小的数?
def get_min_pos(li):
min_pos = 0
for i in range(1, len(li)):
if li[i] < li[min_pos]:
min_pos = i
return min_pos
那么选择排序的代码思路大概就出来了:
from cal_time import *
import random
@cal_time
def select_sort(li):
for i in range(len(li)-1): # n或者n-1趟
# 第i趟无序区范围 i~最后
min_pos = i # min_pos更新为无序区最小值位置
for j in range(i+1, len(li)):
if li[j] < li[min_pos]:
min_pos = j
li[i], li[min_pos] = li[min_pos], li[i]
li = list(range(10000))
random.shuffle(li)
select_sort(li)
时间复杂度:O( n 2 n^2 n2)
稳定性:不稳定
3、插入排序
思路:列表被分为有序区和无序区两个部分。最初有序区只有一个元素。每次从无序区选择一个元素,插入到有序区的位置,直到无序区变空。
原理可以参考博客:排序算法 | 插入排序算法原理及实现和优化
代码实现:
from cal_time import *
import random
@cal_time
def insert_sort(li):
for i in range(1, len(li)): # i 为某元素下标
tmp = li[i] # 某元素
j = i -1
while j >= 0 and li[j] > tmp # 只要往后挪就循环 2个条件都得满足
# 如果j=-1 停止挪动 如果li[j]小了 停止挪动
li[j+1] = li[j]
j -= 1
# j位置在循环结束的时候要么是-1,要么是一个比tmp小的值
li[j+1] = tmp # 把某元素放到j+1的位置上
li = list(range(10000))
random.shuffle(li)
insert_sort(li)
时间复杂度:O( n 2 n^2 n2)
笔者在这解释一句代码:
while j >= 0 and li[j] > tmp
大多数人while里面不喜欢使用and,当然这句话可以改成while+if判断。只不过这里这样写比较整洁。但是建议and前后两条语句的顺序不要改变。虽然在这行代码中,and前后语句颠倒不会对结果造成影响,但在其他某些场合,and前后语句顺序会直接影响运行结果。
介绍一个可能大多数人学Python都忽略掉的地方:
布尔语句的短路功能
比如:不使用if关键字,也不能用while,要写出一个具有if功能的句子。
完成:a 大于0 就输出,不大于0就不输出。
输入:
a = 2
s = "Hello"
a>0 and print(s)
a = -2
s = "Hello"
a>0 and print(s)
输出:

and触发布尔语句的短路:and前面是True,后面也要继续计算;and前面是False,后面就不需要计算了。
True or …
False and …
回到这行代码:
while j >= 0 and li[j] > tmp
Python语言可以解释列表索引 j = -1 ,但是其他的语言不可以。所以笔者建议如果使用其他语言的while语句,其中有and的时候需要考虑布尔语句的短路特性,防止程序异常,养成良好的编程习惯很重要~
其他场合下的and 的前后语句顺序问题也需要着重留意。
