【布隆过滤器】Set Membership Testing using Bloom Filter
Presentation
Introduction
The Bloom filter is a simple random binary data structure which can be efficiently used for approximate set membership testing. When testing for membership of an object, the Bloom filter may give a false positive, whose probability is the main performance figure of the structure.1
A Bloom filter is a space-efficient probabilistic data structure, conceived by Burton Howard Bloom in 1970, that is used to test whether an element is a member of a set.False positive matches are possible, but false negatives are not – in other words, a query returns either “possibly in set” or “definitely not in set”. Elements can be added to the set, but not removed (though this can be addressed with a “counting” filter); the more elements that are added to the set, the larger the probability of false positives.
1.Algorithm description
1.1Initialization
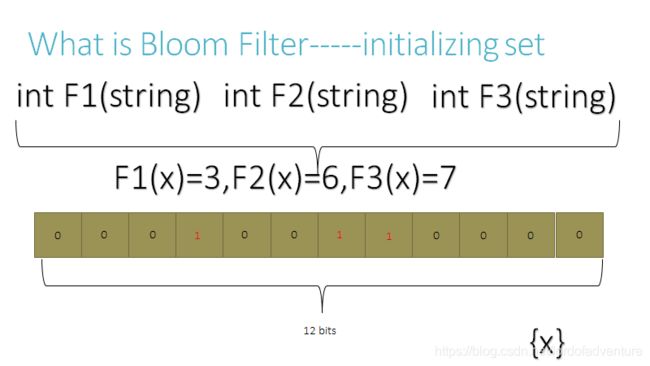
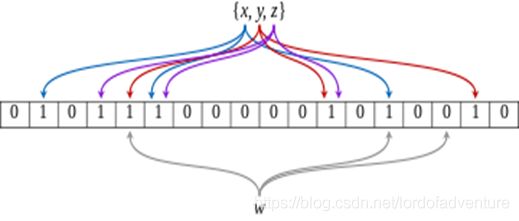
An empty Bloom filter is a bit array of m bits, all set to 0. There must also be k different hash functionsdefined, each of which maps or hashes some set element to one of the m array positions, generating a uniform random distribution. Typically, k is a constant, much smaller than m, which is proportional to the number of elements to be added; the precise choice of k and the constant of proportionality of m are determined by the intended false positive rate of the filter.
1.2Add an element to the set
To add an element, feed it to each of the k hash functions to get k array positions. Set the bits at all these positions to 1.
1.3Test an element
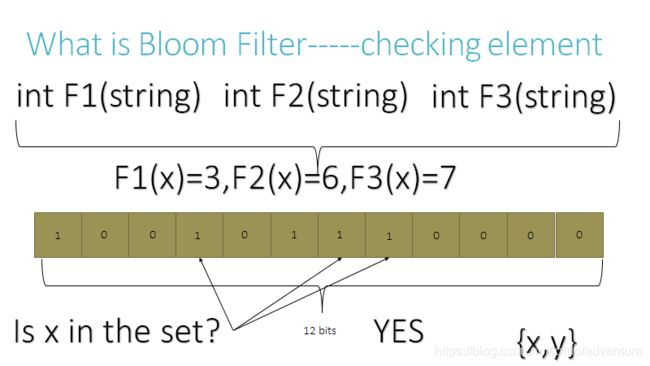
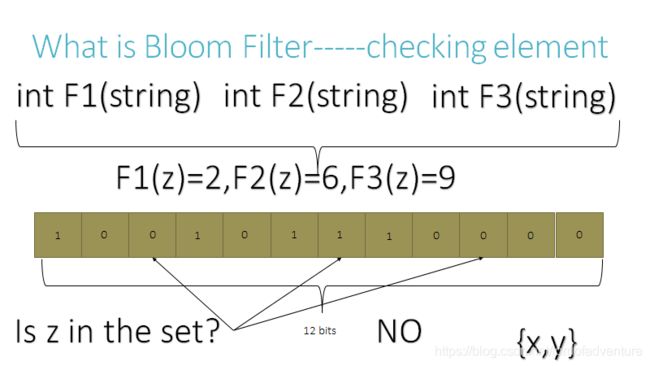
To query for an element (test whether it is in the set), feed it to each of the k hash functions to get k array positions. If any of the bits at these positions is 0, the element is definitely not in the set – if it were, then all the bits would have been set to 1 when it was inserted. If all are 1, then either the element is in the set, or the bits have by chance been set to 1 during the insertion of other elements, resulting in a false positive. In a simple Bloom filter, there is no way to distinguish between the two cases, but more advanced techniques can address this problem.
2.Analysis
2.1Faster Time&Smaller Space
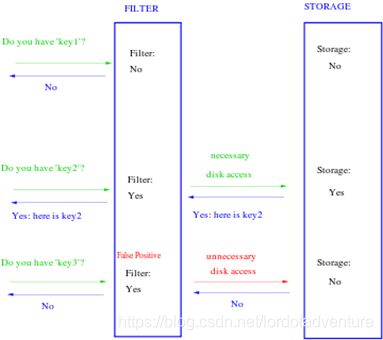
Bloom proposed the technique for applications where the amount of source data would require an impractically large amount of memory if “conventional” error-free hashing techniques were applied. He gave the example of a hyphenation algorithm for a dictionary of 500,000 words, out of which 90% follow simple hyphenation rules, but the remaining 10% require expensive disk accesses to retrieve specific hyphenation patterns. With sufficient core memory, an error-free hash could be used to eliminate all unnecessary disk accesses; on the other hand, with limited core memory, Bloom’s technique uses a smaller hash area but still eliminates most unnecessary accesses. For example, a hash area only 15% of the size needed by an ideal error-free hash still eliminates 85% of the disk accesses.
2.2Low Mistaken Rate
More generally, fewer than 10 bits per element are required for a 1% false positive probability, independent of the size or number of elements in the set.

2.3Bloom Filter Parameters

We could easily plot these on a graph, with the X axis showing the number of elements and the Y axis false positive probability. In this picture we can see that the larger the number of hash functions, the smaller the error rate. When we use only 24 hashes, we can handle 100,000 levels of data, and the error rate is very small. When we have 36 hashes, we can handle billions of levels of data.
3.Application
Bloom filters are not only widely used for processing large amounts of data, but also for speeding up hard disk reading and writing.
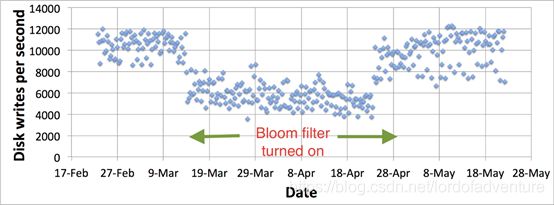
The provenance of the image is a web server. As you can see , when we turn on the Bloom Filter, Disk writes per second almost become half of the original status which means we can solve twice the amount of data with the same hardware devices.
Now the world giant network company all are using Bloom Filter. Google Bigtable, Apache HBase and Apache Cassandra, and Postgresql use Bloom filters to reduce the disk lookups for non-existent rows or columns. Avoiding costly disk lookups considerably increases the performance of a database query operation. Bitcoin uses Bloom filters to speed up wallet synchronization. We can even use it for Chemical structure searching.
4.Disadvantages and Optimizaiton
4.1False Positives
It is often the case that all the keys are available but are expensive to enumerate (for example, requiring many disk reads). When the false positive rate gets too high, the filter can be regenerated; this should be a relatively rare event.
4.2Removing Operation
Removing an element from this simple Bloom filter is impossible because false negatives are not permitted. An element maps to k bits, and although setting any one of those k bits to zero suffices to remove the element, it also results in removing any other elements that happen to map onto that bit. Since there is no way of determining whether any other elements have been added that affect the bits for an element to be removed, clearing any of the bits would introduce the possibility for false negatives.
Using counting bloom filter can make the removal operation possible, it replace each bit to several bits in the original simple bloom filter, and each time an element is added, the related position increase by 1,and each time an element is removed the position is decreased by 1.2
5.Recent Studies
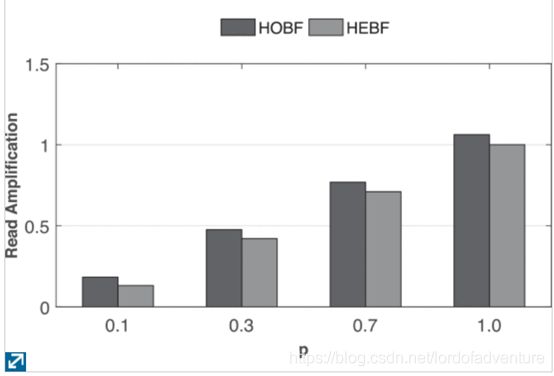
Researchers optimize structure of Bloom Filter to read and write better, they propose a new data structure called Grouped Level Structure (GLS) to reduce write amplification3
Some splits each target string into two substrings and considers the second substring for programming the BF. The objective is to minimise the false positive rate by maximising the common hash signatures from the second substring. Results show that compared to the traditional means of using BFs, the proposed approach reduces the false positive rate by averages of 76 and 88% for 32 and 64 Kb BFs, respectively.4
Some propose a novel Dual Counting Bloom Filter (DCBF) data structure to decrease false detection of matching packets applicable for the SACK.5
Other research finds a way to save 37% of space overhead, compared with state-of-the-art techniques. The new BF is called The TSA-BF which consists of two parts: a segmented aging BF algorithm (SA-BF) and a ternary prefix-tagging encoder (TPE). In an environment with the ternary prefix-rules, the TSA-BF can save another 93% of space overhead, compared with the best-performance scheme. 6
6.Conclusions
A Bloom Filter can solve set membership testing problem at faster speed and using smaller space while it sacrifice some accuracy. A Bloom Filter may make a mistake called false positives but the probabilities can be proved to be small. Currently, Bloom Filter is still being studied, mostly applying it to some network projects and the optimization of Bloom Filter is still being studied on minimizing the mistaken rate and make it faster and smaller.
Q&A
Q1:
How does bloom filter deal with cache penetration problem
A1:
As we know, Bloom Filter can judge a element whether is in a set, we can use it to examine a data whether in our cache, when our Bloom filter find a IP address continuous visit data over a period time ,then we will prohibited access to this ip to protect our database.
Q2:
We know that one bit can only represent 0 or 1, so in the counting Bloom Filter, how can you represent a number more than 1, and will that cost a lot more space? How can you balance between space and efficiency?
A2:
Well using one bit alone truly cannot represent a number, so we should use more than one bit to count. This will use more space. To balance between space and efficiency, we can set a limit on each position that it cannot count more than, for example, 7 times(which use 3 bit)
Q3:
Since it seems that the more hash function we use, the error rate may be reduced, what if when the data size grows bigger than what we expected, how can we add some hash function to the Bloom Filter?
A3:
I’m sorry to answer that you have to rebuild the bloom filter, there is currently no such method to simply add a hash function into it.
References
Fabio Grandi:On the analysis of Bloom filters. Inf. Process. Lett.129:35-39(2018) ↩︎
Fan, Li; Cao, Pei; Almeida, Jussara; Broder, Andrei(2000),"Summary Cache: A Scalable Wide-Area Web Cache Sharing Protocol",IEEE/ACM Transactions on Networking,8(3): 281–293,doi:10.1109/90.851975 ↩︎
Weitao Zhang,Yinlong Xu,Yongkun Li,Yueming Zhang,Dinglong Li:
FlameDB: A Key-Value Store With Grouped Level Structure and Heterogeneous Bloom Filter. IEEE Access 6:24962-24972(2018) ↩︎Shervin Vakili,J. M. Pierre Langlois,Yvon Savaria,Naraig Manjikian:Enhanced Bloom filter utilisation scheme for string matching using a splitting approach. IET Communications12(7):868-875(2018) ↩︎
Ivica Dodig,Vlado Sruk,Davor Cafuta:Reducing false rate packet recognition using Dual Counting Bloom Filter.Telecommunication Systems68(1):67-78(2018)
[6] Sheng-Chun Kao,Ding-Yuan Lee, Ting-Sheng Chen,An-Yeu Wu: ↩︎Dynamically Updatable Ternary Segmented Aging Bloom Filter for OpenFlow-Compliant Low-Power Packet Processing. IEEE/ACM Trans. Netw.26(2):1004-1017(2018) ↩︎