基于S型曲线的连续多段曲线插补平滑过渡的规划算法(Matlab)
写在前面
前面的博客已经写了关于空间直线与空间圆弧的常用插补算法,而这些都是单一路径,实际中并不实用。对于连续多段路径,传统方法是将多段路径细分,然后对每段路径采用首尾速度为0的加减速算法(S型曲线或梯形曲线),这就带来了频繁启停的问题,容易对机械臂造成冲击,同时运行时间较长。
下面我把前面博客中提到的非对称S型加减速算法与空间中多段路径相结合,实现多段路径平滑过渡,减少运行时间。简单画一个轮廓状的“S”字符:
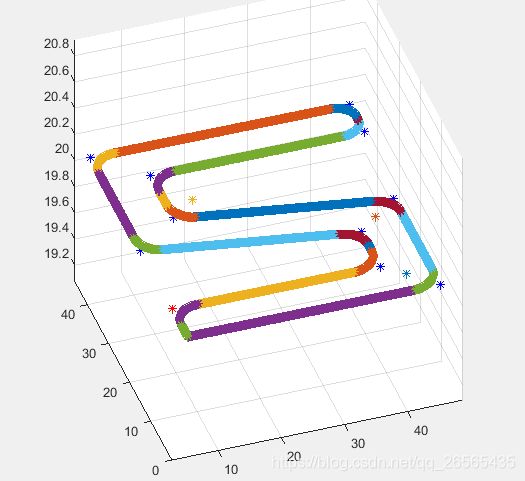
本文方法:
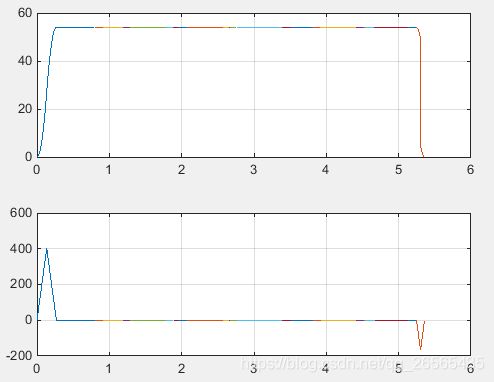
速度与加速度曲线:
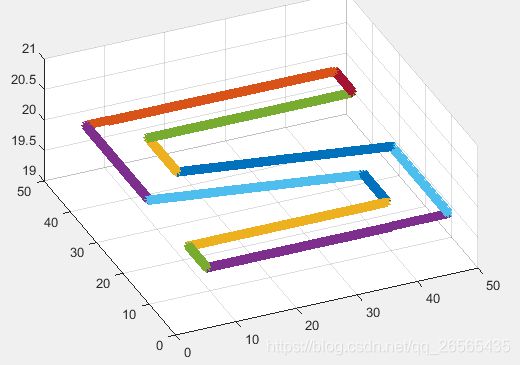
采用分段路径首尾速度为0的加减速控制方法:
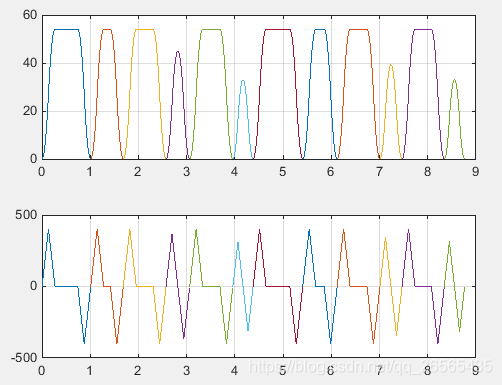
速度与加速度曲线:
对比结果还是很明显滴~本文的方法运行时间更短了,没有频繁启停,轮廓曲线更圆滑。如果在加上动力学方面的约束,就更好了。这个以后再讨论。
预处理
“预处理”,顾名思义就是拿到了一个轮廓轨迹,先想想这个轨迹如何分段,分段后如何衔接。
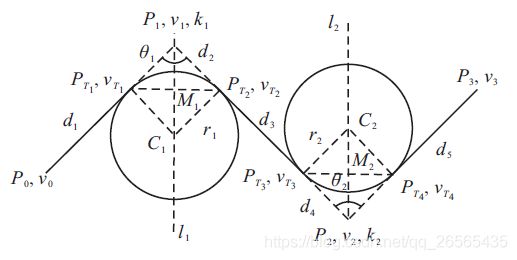
一般工业机器人任务空间的运动轨迹都是由圆弧段和直线段组成的,对于多段连续直线路径而言,任意两段相连直线段的连接处需要平滑处理,这里选择建立圆弧模型进行路径拐角过渡。下面给出圆弧模型的建立过程:
P i P_{i} Pi, v i , v_{i}, vi, r i r_{i} ri分别为用户设定的拾放路径目标点、速度和过渡半径; P T i P_{Ti} PTi, v T i v_{Ti} vTi, C i C_{i} Ci分别为圆弧转接点、转接点的速度和圆心; M i M_{i} Mi为两圆弧转接点的中点; θ i \theta_{i} θi, l i l_{i} li 分别为拐角大小和角平分线; d i d_{i} di为分割后的小路径段长度。
针对由 P 0 P_{0} P0, P 1 P_{1} P1, P 2 P_{2} P2构成的路径段转接模型,设计求解步骤为:
Matlab函数如下:
% 拾取放置操作分段路径转接模型
% 参数: 用户设定的三个拾放路径点P0,P1,P2的位置
% 过渡半径r
% 最大加速度Amax
% 插补周期t
% 返回值: 转接点Pt1,Pt2,分割后的小路径长度d1,d2,圆心C,圆心角theta
%
function [Pt1, Pt2, d1, d2, C, theta] = PathSegmentTrans(P0, P1, P2, r, t)
% 求拐角theta
P1P0 = sqrt(power(P0(1) - P1(1), 2) + power(P0(2) - P1(2), 2) + power(P0(3) - P1(3), 2));
P1P2 = sqrt(power(P2(1) - P1(1), 2) + power(P2(2) - P1(2), 2) + power(P2(3) - P1(3), 2));
vec_P1P0 = [P0(1) - P1(1), P0(2) - P1(2), P0(3) - P1(3)];
vec_P1P2 = [P2(1) - P1(1), P2(2) - P1(2), P2(3) - P1(3)];
theta = acos((dot(vec_P1P0, vec_P1P2)) / (P1P0*P1P2));
% 求转接点Pt1、Pt2
vec_P1Pt1 = (r/tan(theta/2)/P1P0) * vec_P1P0;
vec_P1Pt2 = (r/tan(theta/2)/P1P2) * vec_P1P2;
Pt1 = P1 + vec_P1Pt1;
Pt2 = P1 + vec_P1Pt2;
% 求路径长度d1、弧长d2
d1 = sqrt(power(Pt1(1) - P0(1), 2) + power(Pt1(2) - P0(2), 2) + power(Pt1(3) - P0(3), 2));
d2 = (pi - theta) * r;
% % 求转接速度vt
% 这是考虑机械系统动力学匀速因素得到的转接速度
% a = sqrt(Amax * r);
% b = d2 / t;
% if (a > b)
% vt = b;
% else
% vt = a;
% end
% 求圆心C
vec_Pt1M = (1/2) * (Pt2 - Pt1);
M = Pt1 + vec_Pt1M;
vec_P1M = M - P1;
P1M = sqrt(power(M(1) - P1(1), 2) + power(M(2) - P1(2), 2) + power(M(3) - P1(3), 2));
P1C = r / sin(theta/2);
vec_P1C = (P1C / P1M) * vec_P1M;
C = P1 + vec_P1C;
end
基于非对称S曲线的轨迹规划
核心方法:机器人学回炉重造(6):关节空间规划方法——梯形加减速(与抛物线拟合的线性函数)、S型曲线规划
一些文献中给S型曲线加了很多修饰词,比如非对称、带约束啥的,其实就是我上面那篇博客的S曲线,首尾速度可以不一样,带有位移、速度以及加速度约束。
下面这幅图中, T 1 T_{1} T1 ~ T 3 T_{3} T3对应路径段 P 0 P T 1 P_{0}P_{T1} P0PT1 ,分为加加速段、匀加速段、减加速段和匀速段; T 4 T 5 T_{4}T_{5} T4T5 对应过渡圆弧 P T 1 P T 2 P_{T1}P_{T2} PT1PT2,为匀速运动; T 6 T_{6} T6 ~ T 9 T_{9} T9对应路径段 P T 2 P T 3 P_{T2}P_{T3} PT2PT3,分为减加速段、匀减速段、减减速段和匀速段。把下面这幅图和上面那篇博客中的S曲线对照着看,容易理解直线段 d i d_{i} di(i为奇数,1,3,5,……)均为加速段或者减速段,圆弧段 d i d_{i} di(i为偶数,2,4,6,……)均为匀速段,并且对于直线段而言,其最大速度为圆弧连接点的速度 v T i ( v T i = v T i + 1 ) v_{Ti}(v_{Ti}=v_{Ti+1}) vTi(vTi=vTi+1)。
对每段 P i P i + 1 P i + 2 P_{i}P_{i+1}P_{i+2} PiPi+1Pi+2进行S曲线加减速规划,得到转接点速度,也就是规划得到的曲线实际能够达到的最大速度vlim,Matlab函数如下:
% 获取转接运动参数(速度)
% 参数: 分段路径长度d1,d2,d3
% P0、P1、P2的速度v0, v1, v2(P1为中间点)
% 最大加速度amax,最大加加速度jmax
% 返回值: 转接点速度vt(即为路径上能够达到的最大速度)
function [vt] = TransMotionPara(d1, d2, d3, v0, v1, v2, amax, jmax)
% 得到规划参数Ta, Tv, Td, Tj1, Tj2, q0, q1, v0, v1, vlim, amax, amin, alima, alimd, jmax, jmin
q0 = 0; q1 = d1 + d2 + d3
para = STrajectoryPara(q0, q1, v0, v2, v1, amax, jmax);
vt = para(10);
end
插补
这里先只讲位置插补
预处理过后,轨迹就分段成为了一大堆直线段和一大堆圆弧段,这里要做的就是对这些空间直线和空间圆弧进行插补,于是又回到老话题了……
这里直线段插补不多说,和前面博客中提到的一样,空间单一直线位置插补+ S型加减速曲线归一化处理,具体方法见基于带约束S型加减速曲线的空间直线插补与空间圆弧插补算法(Matlab)
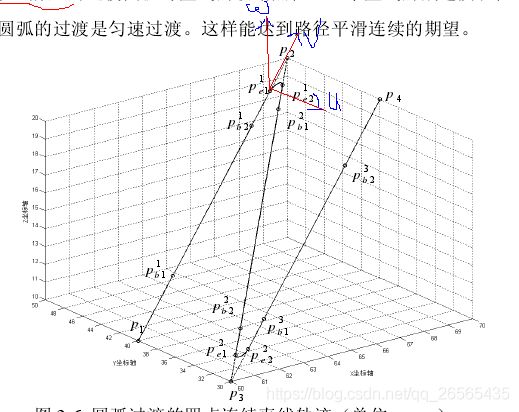
圆弧段插补也大同小异,方法有所不同,但基本是采用局部坐标系的空间圆弧插补方法和齐次坐标变换原理。新建立的局部坐标系UVW如下图所示,下面图中点的下标和我上面写的有些不一样,忽略所有 P b i P_{bi} Pbi并将 P e i P_{ei} Pei看成 P T i P_{Ti} PTi就行了,我就没有重新画图了。以第一段轨迹为例,新坐标系建立过程如下:
以 P T 1 P_{T1} PT1为原点, P 0 P 1 → \overrightarrow{P_{0}P_{1}} P0P1为V轴, P 2 P 1 → × P 1 P 0 → \overrightarrow{{P_{2} P_{1}}} \times \overrightarrow{P_{1} P_{0}} P2P1×P1P0为W,
V轴单位向量为: V = P 0 P 1 → ∣ P 0 P 1 → ∣ V=\frac{\overrightarrow{P_{0} P_{1}}}{\left|\overrightarrow{P_{0} P_{1}}\right|} V=∣∣∣P0P1∣∣∣P0P1
W轴单位向量为: W = P 2 P 1 → × P 1 P 0 → ∣ P 2 P 1 → × P 1 P 0 → ∣ W=\frac{\overrightarrow{{P_{2} P_{1}}} \times \overrightarrow{P_{1} P_{0}}}{\left|\overrightarrow{{P_{2} P_{1}}} \times \overrightarrow{P_{1} P_{0}}\right|} W=∣∣∣P2P1×P1P0∣∣∣P2P1×P1P0
U轴单位向量为: U = V × W U=V \times W U=V×W
在新坐标系UVW上圆弧过渡段的插补点坐标 ( x i , y i , z i ) (x_{i},y_{i},z_{i}) (xi,yi,zi)坐标值为:
x i = r i − r i ⋅ cos ( v t i ⋅ t r i ) y i = r i ⋅ sin ( v t i ⋅ t r i ) z i = 0 \begin{array}{c}{x_{i}=r_{i}-r_{i} \cdot \cos \left(\frac{vt_{i} \cdot t}{r_{i}}\right)} \\ {y_{i}=r_{i} \cdot \sin \left(\frac{vt_{i} \cdot t}{r_{i}}\right)} \\ {z_{i}=0}\end{array} xi=ri−ri⋅cos(rivti⋅t)yi=ri⋅sin(rivti⋅t)zi=0
其中, r i r_{i} ri为设定的该段圆弧的半径参数, v t i vt_{i} vti为规划得到的过渡圆弧速度.
然后就是老生常谈的话题,把局部新坐标系中的圆弧通过左乘该坐标系相对基座标系的齐次变换矩阵从而变换回原来的XYZ值。
Matlab函数如下,我在函数中留了姿态插补四元数参数的位置,留着以后加姿态插补用:
% 过渡圆弧的插补算法,搭配ContinueSpaceLine使用
% 参数: Pt1,Pt2,P1(Pt1和Pt2的中间点),Qt1,Qt2
% 过渡圆弧弧长d、过渡半径r、插补周期t
% 圆弧插补速度vt
% 返回值: 插补点数N,插补时间Tt
function [x y z qk N Tt] = Transition_arc(Pt1, Pt2, P1, Qt1, Qt2, d, r, t, vt)
% 建立新坐标系UVW
% 新坐标轴V
vec_Pt1P1 = P1 - Pt1;
Pt1P1 = sqrt(power(P1(1) - Pt1(1), 2) + power(P1(2) - Pt1(2), 2) + power(P1(3) - Pt1(3), 2));
V = (1/Pt1P1) * vec_Pt1P1;
ox = V(1); oy = V(2); oz = V(3);
% 新坐标系W
vec_Pt2P1 = P1 - Pt2;
vec_W_ = cross(vec_Pt1P1, vec_Pt2P1);
W_ = sqrt(power(vec_W_(1), 2) + power(vec_W_(2), 2) + power(vec_W_(3), 2));
W = (1/W_) * vec_W_;
ax = W(1); ay = W(2); az = W(3);
% 新坐标系U
U = cross(V, W);
nx = U(1); ny = U(2); nz = U(3);
% 相对于基座标系{O-XYZ}, 新坐标系{C-UVW}的坐标变换矩阵
T = [nx ox ax Pt1(1);
ny oy ay Pt1(2);
nz oz az Pt1(3);
0 0 0 1];
% 计算两个四元数之间的夹角
dot_q = Qt1.s*Qt2.s + Qt1.v(1)*Qt2.v(1) + Qt1.v(2)*Qt2.v(2) + Qt1.v(3)*Qt2.v(3);
if (dot_q < 0)
dot_q = -dot_q;
end
% 插补时长
Tt = d / vt;
i = 1;
for j = 0: t: Tt
% 位置插补
x_(i) = r - r * cos(vt*j/r);
y_(i) = r * sin(vt*j/r);
P = T*[x_(i); y_(i); 0; 1];
x(i) = P(1);
y(i) = P(2);
z(i) = P(3);
% 单位四元数球面线性姿态插补
% 插值点四元数
if (dot_q > 0.9995)
k0 = 1-t;
k1 = t;
else
sin_t = sqrt(1 - power(dot_q, 2));
omega = atan2(sin_t, dot_q);
k0 = sin((1-t)*omega) / sin(omega);
k1 = sin(t*omega) / sin(omega);
end
qk(i) = Qt1 * k0 + Qt2 * k1;
N = i;
i = i + 1;
end
end
字符轮廓提取
CAD中画50mm*50mm的栅格图,在栅格图内绘制字体轮廓,然后提取关键点坐标。
以栅格左下角的点作为坐标原点,以水平方向为X轴,以垂直方向为Y轴建立平面直角坐标系,字符“S”的关键点坐标如图所示
提取坐标原点O的坐标值,然后用其他关键点的坐标值减去原点的,就能得到这些关键点在当前栅格坐标系下的坐标值,如下表
| 关键点 | A | B | C | D | E | F | G | H | I | J | K | L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X | 5 | 45 | 45 | 12 | 12 | 46 | 46 | 5 | 5 | 38 | 38 | 5 |
| Y | 0 | 0 | 22 | 28 | 39 | 39 | 45 | 46 | 22 | 16 | 7 | 7 |
ok完事儿~
拼起来
是的,最后总的程序就是把上面分段规划得到的一堆直线插补点和一堆圆弧插补点,按照时间顺序拼起来。总程序我就不放了,仁者见仁智者见智。
参考文献
[1]王斌锐,王涛,李正刚,陈立,陈迪剑.多路径段平滑过渡的自适应前瞻位姿插补算法[J].控制与决策,2019,34(06):1211-1218.
[2]陈伟华. 工业机器人笛卡尔空间轨迹规划的研究[D].华南理工大学,2010.
[3]类延超. 五自由度写字机器人系统研究[D].山东大学,2012.
[4]王涛,陈立,郭振武,王斌锐,李振娜.基于圆弧转接和跨段前瞻的拾放操作轨迹规划[J/OL].计算机集成制造系统:1-13[2019-08-09]
2019.12.8
发现一处问题:
子程序Transition_arc中原 k0 = sin((1-t*omega)) / sin(omega);修改为 k0 = sin((1-t)*omega) / sin(omega);
写算法不易,要点积分ok把~
很多朋友需要代码,每次发邮件也挺费劲,所以我就上传了文档供大家下载,仅供思路参考哈~
这只是matlab理论代码,还是有很多bug的,实际运用写成c还是要根据实际情况修改很多很多。我的邮箱是[email protected],欢迎大家和我交流!
下载链接如下:
https://download.csdn.net/download/qq_26565435/12630819