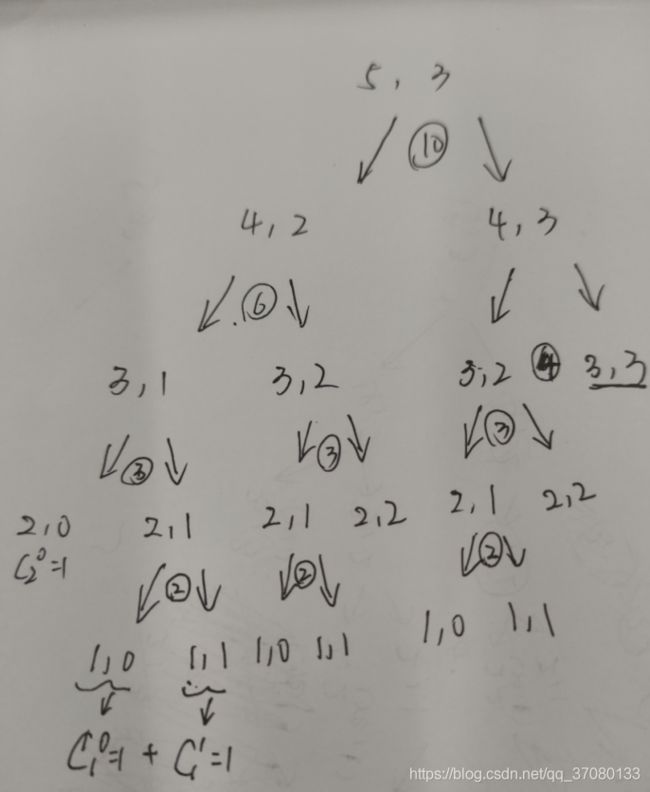卜若的代码笔记-算法实验室-九:递归搜索(一)
1 名字是我自己取的,主要是比较形象,先来看原题
比如讲,一组数据如
[7,1,5,3,6,4]你需要找出哪天买入,哪天卖出,从而获取最大收益。
这个过程是一个粘性搜索,比如,你第一天以7元一股买入了股票,然后,你需要在接下来的[1,5,3,6,4]的某一天卖出,获取收益,获取了之后,你希望继续寻找下一次出手的机会
如果用图像来进行表达就是
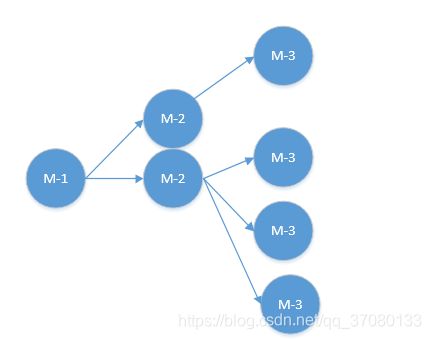
第n天买入:
(存在收益时) 第n+x天卖出:
第n+x+1天买入
(存在收益时)第n+x+1+x2天卖出
....
这样,你会不断的往下搜索(递归方式),你就会获得很多种收益方式,我们选取其中最大的收益方式,就能去解决这个问题。
这样理解起来还是太麻烦了
现在,我把这个问题重新换一下,对于
[7,1,5,3,6,4]这样一组数据,我第一天买的时候,我有几种收益方式?
0种是吧
第二天买时,有几种收益方式呢?我们将p表示买入,s表示卖出,n表示不作操作
那就是
1.p-s-p-s-n
2.p-n-s-n-n
3.n-p-n-s-n
...
这是一个组合方式,求组合的方式有...递归?深搜?广搜?
其实吧...都可以。所以我们选择最简单的递归吧!
递归怎么求组合呢?
现在出一道新题,请利用递归的思想
算法2:求出a,b,c,d,e,f的所有组合方式(是组合,不是排列)当然,直接接触这种高端操作本身还是难的
所以还是换一道题
算法3:求1,2,3,4,5的所有长度为3的组合的总数这是一个典型的
![]() 的问题
的问题
应该是概率论里面做了证明C(n,m) = C(n-1,m-1)+c(n-1,m)
至于怎么证的,自己去翻概率论,也许我有心情会在这个系列的某一篇写
这是一个十分重要的公式,所以说,数学是编程的基础,没见过这个公式,基本上不可能将这个递归求组合的问题搞定
当我们拥有这样一个地推式了之后,我们可能还需要考虑一些问题,当然,这些问题的抛出不是一下就能想到的,多看书,你会知道的:
当n == m时,有多少种组合?答案是1种
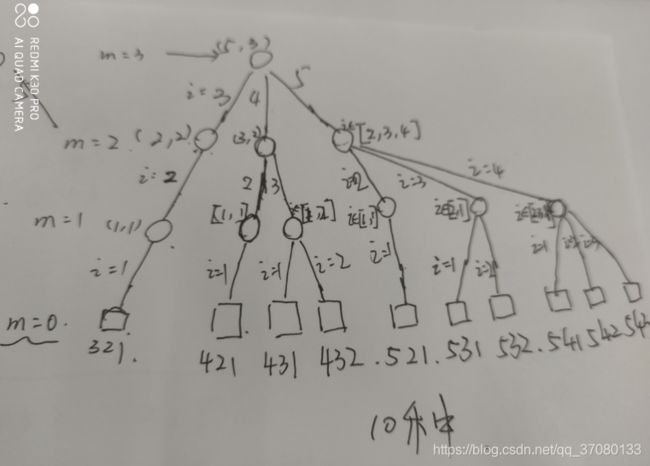
当n 当n>m时,有多少种组合?答案是不知道,得按照公式继续推 当m==0时,应该有多少种组合?也就是 如果你对递归比较熟悉,那就知道,递归存在边界条界,也就是无法递推的最最小单元,当n ==m,n 我们就能画出一张递推图: 根据这个递推图,我们可以看到 这个时候,你就能狗实现递推算法如下: 当然还有另外一种算法:同样是基于递归的,我先做一件事情: 固定m-1个数 搜索m-2个数的所有可能 搜索m-3个数的所有可能 ... 达到递归处理的边界 得到一张类似于这种的图: 边界条件是layer = m,当m = 3时,也就是希望求取长度为3的组合时,可以发现,边界条件就是m-3 = 0 当然,这个时候,如果你使用递归的话,那就是(m-1) == 0 先来看源码:里面写了注释,就不多解释了,同时,我将f(5,3)的所有组合结果绘制了一张图: 这样,我们就可以通过递归去求解这种组合。 下一章,我们回过来讲解一开始抛出的这一道题 ![]() = ?答案是1,证明过程参考概率论
= ?答案是1,证明过程参考概率论![]() = 10
= 10int len = -1;
int NumCombination(int n,int m)
{
len++;
if(m == 0) return 1;
if(n < m) return 0;
if(n == m) return 1;
else{
int pointSum =NumCombination(n-1,m-1) + NumCombination(n-1,m);
return pointSum;
}
}解释起来比较麻烦,思想就是
static int[] arr2 = new int[3];
void func(int n,int m){
for (int i =m;i<=n;i++){
arr2[m-1] = i;
/*
* 当固定arr2[m-1]时,其所属集合为:m,m+1,m+2,...,n
* 如果你分解过1,2,3,4,5的长度为3的组合,你会发现,首个数字的种类有m = 3个
* 这一点很神奇,接下来,可以通过递归,去判断第二个数,直到m-1==0时,这个时候,
* 是递归最小的处理单元,也就不需要再继续递归下去,相当于
* */
if(m <=1){
//在这里确定最后一个数的所有可能
for (int s =0;s<3;s++){
System.out.print(arr2[3-s-1]);
}
System.out.print("\n");
}else {
func(i-1,m-1);
/**
* 这里其实是可以解释的 当m = 3.n = 5时
* 确认m-1:
* 我的选择范围是(n = 5,m = 3) = [3,4,5],这个时候,我选择i = 3时 ->f(m-1) = 3
* 确认m-2
* (i-1,m-1) = (n = 2, m = 2) = [2] ->f(m-2) = 2 令 i = 2 for(i=2:2)=>
* 确认m-3
* (i-1,m-1) = (n = 1,m = 1) = [1] -> f(m-3) = 1;
* 从而推出第一个结果为321的结果
* ...
* 类似递推
*/
}
}
}