卜若的代码笔记-算法实验室:十:递归搜索(二)交易链问题
1 还是上一章的问题
我们对递归的这种搜索特性其实已经有了了解,那么,这道题,我们就能够绘制出它的搜索树,我们将周期缩短为5天,并在5天中进行交易,那么就有图:
这个时候,你就发现,卖出的时间恰好是买入时间的第2,3,4...n天,这个时候,你就可以递归了,当然,这个树不止递归可以操作,还能深度搜索,广度搜索:
不过我们还是使用递归吧:
int stock(int[] arr,int start){
int earnings = 0;
for (int i =start;i使用这个函数,你会发现,每一次卖出都会获得一个收益:
现在要做一件事情就是:
我们希望能够记录住每一次递归时产生的收益:,这个时候可以通过添加节点进行记录,并通过广度搜索遍历所有节点,从而可以获取得到每一次收益
我们将每一次产生收益(不管是正向收益还是负向收益)都称为一次交易,而整个周期的所有交易组成的链,我们称为交易链,现在,可以通过判断每个交易链的最大结果,从而判断出收益最高的交易方式:
当然,现在这个问题已经被我无限的放大了,但是,我们也更加清楚的理解了利用递归生成树的方法,也了解了,这个过程的交易链
以下是源码:
生成交易树
void stock(int[] arr,int start,RPoint parent){
for (int i =start;i获取交易链(bfs)
List transactionChain ;
void bfs(RPoint sp){
Queue rpq = new LinkedList<>();
rpq.offer(sp);
while (!rpq.isEmpty()){
RPoint s2 = rpq.poll();
if (s2.sons.size() == 0) {
transactionChain.add(s2);
}
for (int i =0;i 这时候,其实思路就非常清晰了,回到问题本身,我们只需要获取最大收益,所以并不需要采集交易链本身,只需要知道,这个子节点在什么情况下最大:
现在,我们将收益变成一个个节点:
e1,e2,e3,e4,e5是五个节点,现在来求它的收益:
e5的收益最好求,可以直接获得,因为只存在一次交易,e2的收益 = e5的收益+本次交易的收益
(如果无法理解,那就先定义一个认识,递归往往是最底层节点先处理,你一定会拿到e5的收益,当你开始递归的时候,最先拿到的一定是e5的收益)
e3的收益仅有本次交易的收益,e4也一样,现在的问题是,e1的最大收益是多少?
问题转化成max(e2,e3,e4)
那么对于e2的收益,应该怎么表达呢?
从前面已经知道,递归本身就是树,而且,最先处理的节点是边界节点,也就是e5,e5最先返回,然后到e2,然后执行e3,e4,所以,只需要对每一次递归的收益进行累加,就能够获得这个分支的所有节点值。
而这个算法本身的难点,难以理解的点,就在于,对于一次交易事件,是分成买入,和卖出的,也就是:
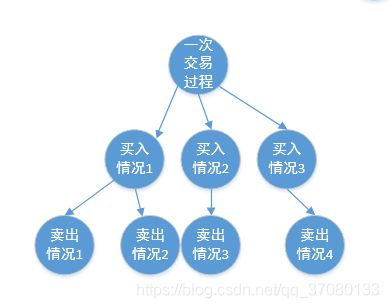
所以,在最小递归单元的条件下,它的交易过程如下:
那么对于这个交易过程的最大收益,就是所有买入的最大收益的最大收益可能,有这一点共识之后,这段代码就很容易理解了:
int stock2(int[]arr ,int start){
int maxBuyEarning = 0;//最大买入收益
for (int i = start;i这就是这道题的暴力解法,有很多值得学习的东西,题号是122,被归类为简单类型,这是因为这道题本身有技巧,下一章会说。