用C++和邻接矩阵实现图算法——图算法有手就行
文章目录
- 1. 图的介绍
- 1.1 图到底是个什么东西
- 1.2 图到底用来干嘛
- 1.3 为什么要有图
- 2. 图的概念介绍
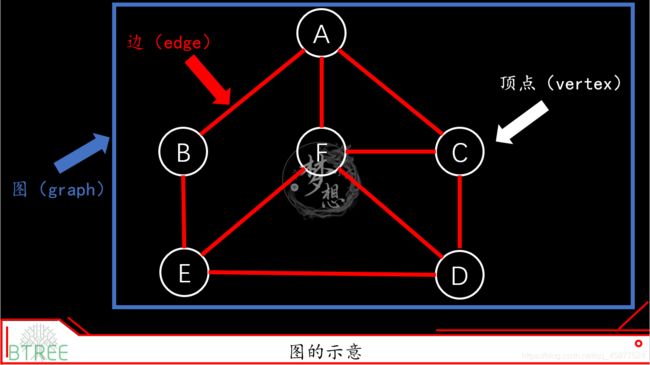
- 2.1 顶点和边(vertex and edge)
- 2.2 权重(weight)
- 2.3 路径与最短路径(path and the shortest path)
- 2.4 连通图/连通分量(connected graph/connected component)
- 2.5 环(loop)
- 2.6 有向图与无向图(Directed Graph and Undirected Graph)
- 2.7 顶点的度
- 2.8 稀疏图和稠密图(sparse graph and dense graph)
- 3. 图的实现方式
- 4. 邻接链表的实现方式
- 5. 邻接矩阵的实现
- 6. 邻接矩阵和邻接链表的比较
- 7. 邻接矩阵的图算法实现
1. 图的介绍
1.1 图到底是个什么东西
图(graph)按是由顶点(vertex)和连接顶点的边(edges)构成的离散结构。离散数学里面的定义如下:
图G = (V,E)由顶点(或结点)的非空集V和边集E构成,每条边有一个或两个顶点与它相连,这样的顶点称为边的端点。边连接它的端点。
1.2 图到底用来干嘛
图几乎可以用来表现所有类型的结构或系统,从交通网络到通信网络,从下棋游戏到最优流程,从任务分配到人际交互网络,图都有广阔的用武之地。打个比较具体一点的比方:

GPS导航就用到了图的算法。
1.3 为什么要有图
图的提出是为了更好的解决多对多的关系,线性表他仅仅局限于一个直接前驱和一个直接后继的关系,而树也仅仅只能有一个直接前驱也就是父节点。
图论〔Graph Theory〕是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系,用点代表事物,用连接两点的线表示相应两个事物间具有这种关系。
2. 图的概念介绍
为以后介绍图算法,提供背景知识。
2.1 顶点和边(vertex and edge)
上面介绍过了,不多重复,这里给出一些比较精准的定义,装一下b,虽然这个确实没什么用。

2.2 权重(weight)
边的权重(又或者是边的长度),是一个比较核心的概念,即每条边所对应的值。边的权重可以是零甚至可以是负数,比较不是一个真正的地图,给个带权重的简单图看一下。
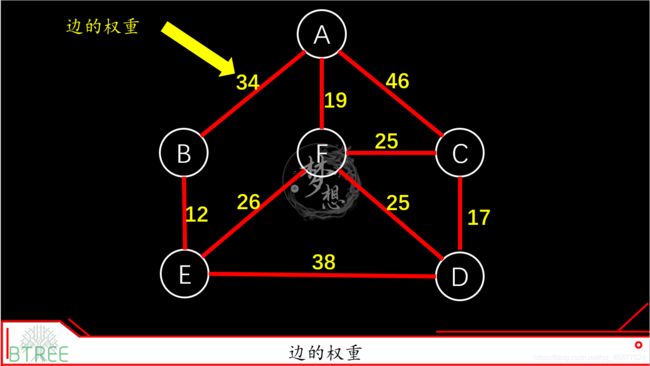
在上面的地图例子中,对应的就是广州到东莞之间的距离(这个距离是我乱写,的不要当真):
2.3 路径与最短路径(path and the shortest path)
在图上任取两顶点,分别作为起点(start vertex)和终点(end vertex),我们可以规划许多条由起点到终点的路线,这个路线就叫做路径,如果两点之间存在路径,那么这两个顶点是连通的。
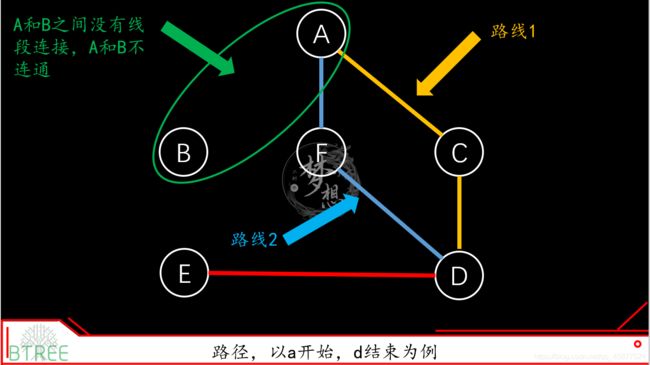
路径也有权重。路径经过的每一条边,沿路加权重,权重总和就是路径的权重(通常只加边的权重,而不考虑顶点的权重),所谓的最短路径就是权重最小的边。
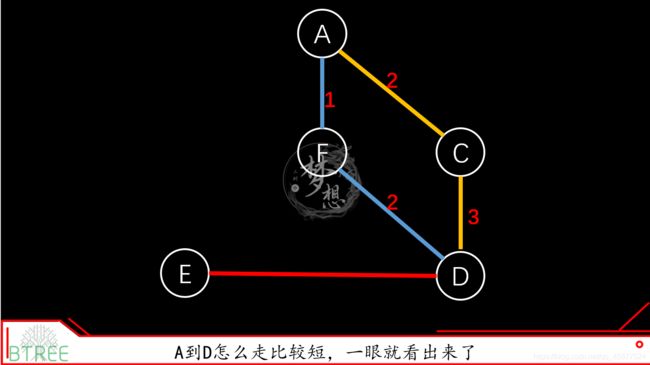
那么,在后面我会用Dijkstra算法来介绍最短路径。
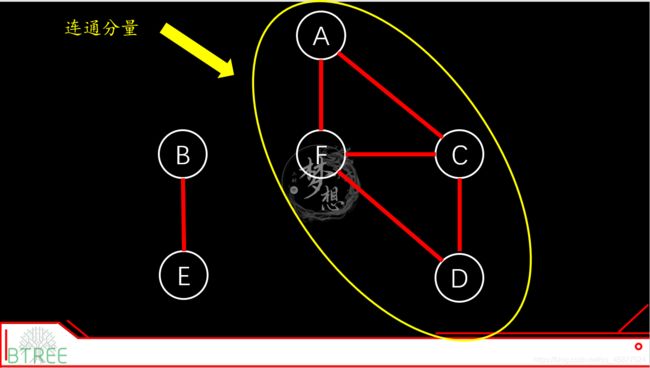
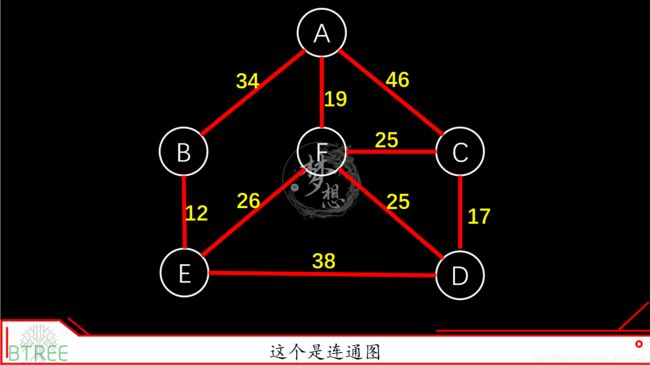
2.4 连通图/连通分量(connected graph/connected component)
每个点之间都存在路径,那么称这个图为连通图。
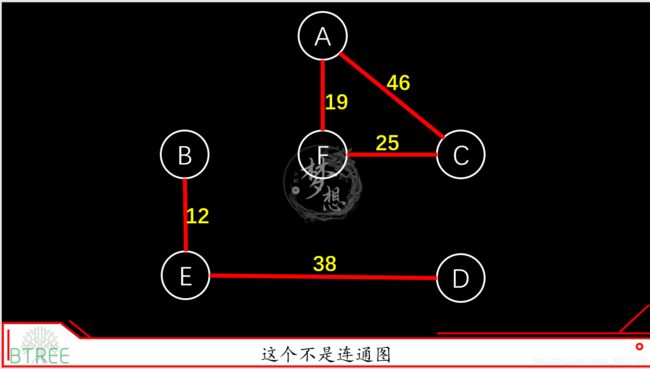
上面那个图,虽然不是一个连通图,但是他有两个连通子图,我们把一个图的最大连通子图称为它的连通分量,连通分量这些特点:
- 是子图
- 子图是连通的
- 子图含有最大顶点数
最大连通子图”指的是无法再扩展了,不能包含更多顶点和边的子图。
2.5 环(loop)
环,也称为环路,是一个与路径相似的概念。在路径的终点添加一条指向起点的边,就构成一条环路。通俗点说就是画圈圈。
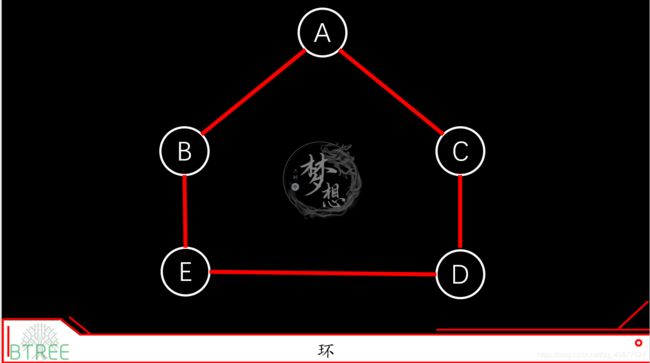

深度优先搜索算法里面用到了环的概念。
2.6 有向图与无向图(Directed Graph and Undirected Graph)
有向图和无向图之间的区别在于方向性,用只有一条边的简单图打个比方,下面这个无向图:
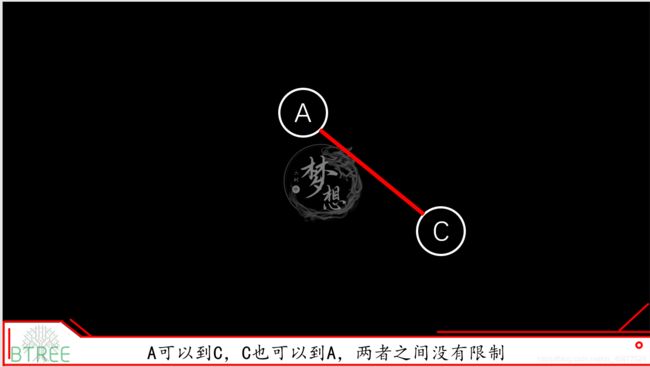
这个是有向图:
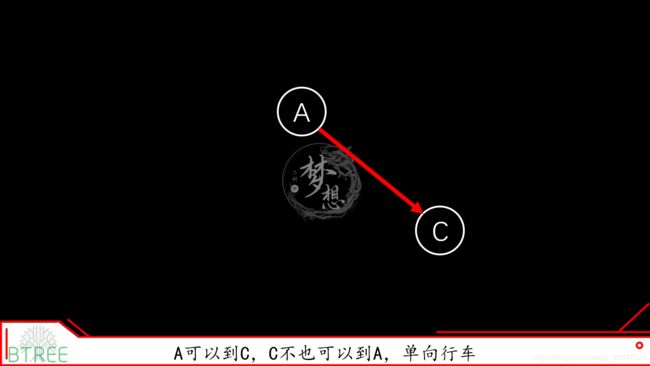
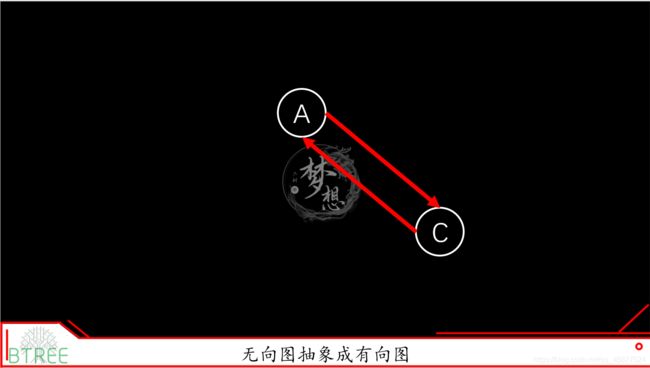
你可以把无向图抽象成这样的有向图:
2.7 顶点的度
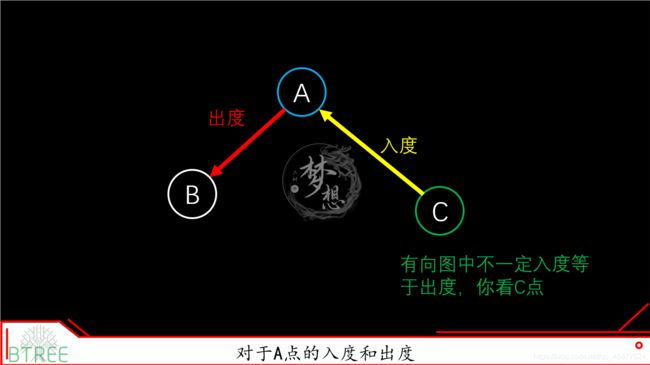
顶点的度,指的是图中和顶点V相关联的边的数目,度 = 入度 + 出度。在有向图中,所谓入度和出度,通俗的讲,入度指的是箭头指向自己这个点,出度指的是箭尾从自己那个点出来。在无向图中,由于没有方向的限制,出度等于入度。
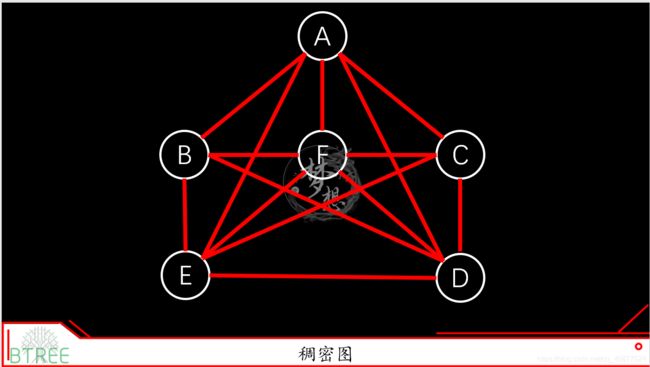
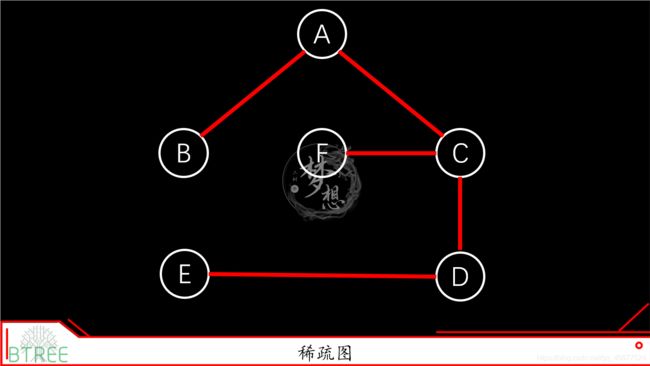
2.8 稀疏图和稠密图(sparse graph and dense graph)
这个说白了就是边多少的问题,最主要是用在图论算法的构建中,时间复杂性和空间复杂性的选择问题,下面是定义
稀疏图:边的条数|E|远远小于顶点V:|V|^2的图
稠密图:边的条数|E|远远接近于顶点V:|V|^2的图
3. 图的实现方式
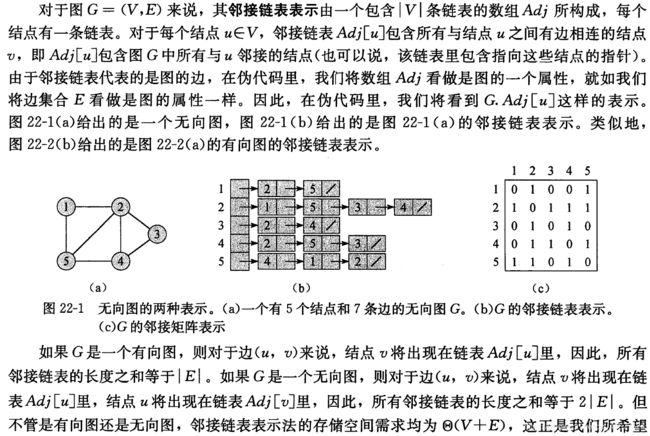
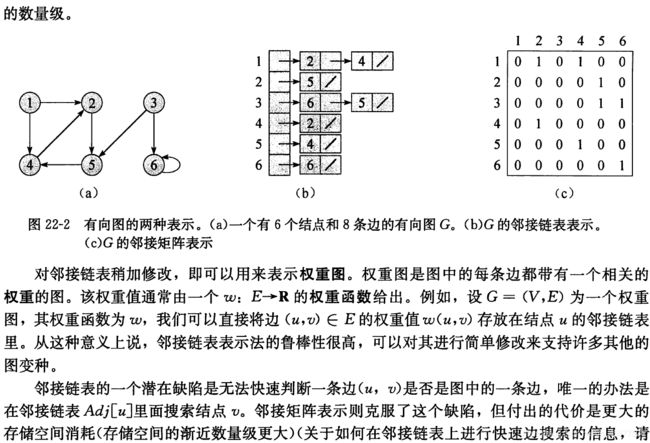
那么好,对于图而言,有两种常见的实现方式:邻接矩阵和邻接链表。那么在leetcode刷题的时候我发现,大部分图算法都是直接在矩阵上面进行,所以我会重点讲解邻接矩阵,邻接链表一笔带过。邻接链表十分直观的把图给表现出来,用链表的形式存储A和指向B的指针,以及边等乱七八糟的,而邻接矩阵是将整个图所在的空间抽象成一个矩阵,在这个矩阵上有点就为1,没点就为0。这里先给出示例图,有点印象。图算法的实现我都是基于无向邻接矩阵,当然我会介绍如何把无向变成有向。



4. 邻接链表的实现方式
邻接链表:
- 对于每个点,存储着一个链表,用来指向所有与该点直接相连的点
- 对于有权图来说,链表中元素值对应着权重
下面是算法导论里面的定义,然后再给出设计思路:
那么好,对于设计好的结点的结构体,应该包含几个元素:
- 自己的字母存储,例如ABCDEFG
- 一个关于边的链表,用来存储与其他点所连接的边的权值
- 在边的结构体那里应该可以指出,两个点是什么,两点确定一条直线,以及下一个边的指针构成一个链表
因此就有了以下示意图:

对着这个示意图进行设计,具体做法:
//头文件:AdjListUndirGraph.h
#ifndef ADJLIST_UNDIR_GRAPH_H //邻接表实现无向图
#define ADJLIST_UNDIR_GRAPH_H
#include //main.cpp
#include "AdjListUndirGraph.h"
int main()
{
char vexs[12]="ABCDEFGHIJK";
AdjListUndirGraph graph(vexs,11,11);
graph.InsertArc(0,1);
graph.InsertArc(0,4);
graph.InsertArc(0,3);
graph.InsertArc(1,2);
graph.InsertArc(1,4);
graph.InsertArc(2,4);
graph.InsertArc(4,5);
graph.InsertArc(5,8);
graph.InsertArc(4,6);
graph.InsertArc(6,7);
graph.InsertArc(3,6);
graph.InsertArc(9,10);
graph.Show();
graph.BFSTraverse();
return 0;
}
5. 邻接矩阵的实现
邻接矩阵:
- 在 n 个顶点的图需要有一个 n × n 大小的矩阵
- 在一个无权图中,矩阵坐标中每个位置值为 1 代表两个点是相连的,0 表示两点是不相连的
- 在一个有权图中,矩阵坐标中每个位置值代表该两点之间的权重,0 表示该两点不相连
- 在无向图中,邻接矩阵关于对角线相等
算法导论的定义:



很烦,很长,我先给出一个示意图解释怎么看邻接矩阵,然后再进行构造思路说明:


边权表和顶点表的读法差不多,先讲顶点表(数字比较简单好看一点):

权值表和它一样的读法,不是∞(∞我这里设置成500)表示两个点所构成的边的值。
那么好,我们设计一个邻接矩阵的类的私有成员,应该包含三个部分:
- 顶点表
- 权值表
- 存储ABCDEFG的字符串
所以,就有了以下类的定义:
//头文件:AdjMatrixUndirNetWork.h
/**
由于Kruskal算法和Prim算法都涉及到一个点以及点附近进行选定最小边的处理,所以我这里将kruskal算法和Prim算法分开放置
对于图的实现而言,通常而言有两种实现方式:一种是邻接矩阵,一种是邻接链表,那么在leetcode的刷题中,
运用到图算法的题目大多采用了,邻接矩阵来实现图,所以这里用邻接矩阵、
**/
#ifndef ADJMATRIX_UNDIR_NETWORK_H
#define ADJMATRIX_UNDIR_NETWORK_H
#define DEFAULT_INFINITY 500
#define DEFAULT_SIZE 10
#include 6. 邻接矩阵和邻接链表的比较
- 邻接矩阵由于没有相连的边也占有空间,因此存在浪费空间的问题,而邻接链表则比较合理地利用空间
- 邻接链表比较耗时,牺牲很大的时间来查找,因此比较耗时,而邻接矩阵法相比邻接链表法来说,时间复杂度低。
- 这个不是性能原因,我看leetcode上面大部分都是用矩阵的形式来解决图算法,所以邻接矩阵的实现比较完整。
7. 邻接矩阵的图算法实现
这里涉及到的一些图算法,不懂的可以看我以往的文章里面有介绍,或者是在B站上搜索BTree-二树,我之前做的视频里面有讲解。具体代码如下:
AdjMatrixUndirNetWork.cpp
/**
文件名:AdjMatrixUndirNetWork.cpp
该文章的原创作者:阿伟加油鸭。首发于CSDN平台,装载请标注博文出处。
网址:
**/
#include "AdjMatrixUndirNetWork.h"
using namespace std;
//构造函数,首先设置一个空图,随后再将vertexNum等乱七八糟的加进去
AdjMatrixUndirNetwork::AdjMatrixUndirNetwork(int vertexMaxNum, int infinite)
{
vexMaxNum = vertexMaxNum; //设置图的范围
vexNum = 0;
arcNum = 0;
infinity = infinite;
vertexes = new char[vexMaxNum]; //顶点表的大小
tag = new VisitStatus[vexMaxNum]; //设置顶点的状态,用于后面的探索过程
//设置邻接矩阵和权值表
arcs = new int* [vexMaxNum];
edges = new int* [vexMaxNum];
for (int i = 0; i < vexMaxNum; i++)
{
arcs[i] = new int[vexMaxNum];
edges[i] = new int[vexMaxNum];
}
}
//那么好对空图进行改造,这是初始化工作
AdjMatrixUndirNetwork::AdjMatrixUndirNetwork(char* vexs, int vertexNum, int vertexMaxNum, int infinite)
{
vexMaxNum = vertexMaxNum;
vexNum = vertexNum;
infinity = infinite;
arcNum = 0;
vertexes = new char[vexMaxNum];
tag = new VisitStatus[vexMaxNum];
arcs = new int* [vexMaxNum];
edges = new int*[vexMaxNum];
for (int i = 0; i < vexMaxNum; i++) {
arcs[i] = new int[vexMaxNum];
edges[i] = new int[vexMaxNum];
}
for (int i = 0; i < vexMaxNum; i++)
{
vertexes[i] = vexs[i];
tag[i] = UNVISIT;
for (int j = 0; j < vexMaxNum; j++) {
arcs[i][j] = infinity;
edges[i][j] = 0;
}
}
}
//析构函数,删除三个表
AdjMatrixUndirNetwork::~AdjMatrixUndirNetwork()
{
if (vertexes != NULL)
delete[] vertexes;
if (tag != NULL)
delete[] tag;
if (arcs != NULL)
delete arcs;
if (edges != NULL)
delete edges;
}
//在空图中插入边
void AdjMatrixUndirNetwork::InsertArc(int vex1, int vex2, int weight)
{
arcs[vex1][vex2] = weight;
arcs[vex2][vex1] = weight;
edges[vex1][vex2] = 1;
edges[vex2][vex1] = 1;
arcNum++;
}
//对图进行展示,如果点的数目为空,那就没有图,那就展示个蛇皮怪
void AdjMatrixUndirNetwork::Display()
{
if (vexNum != 0)
{
cout << "权重图" << endl;
for (int i = 0; i < vexNum; i++)
{
cout << "[ ";
for (int j = 0; j < vexNum; j++)
cout << arcs[i][j] << " ";
cout << "]" << endl;
}
cout << "顶点图" << endl;
for (int i = 0; i < vexNum; i++)
{
cout << "[ ";
for (int j = 0; j < vexNum; j++)
cout << edges[i][j] << " ";
cout << "]" << endl;
}
}
}
//顶点获取,并且顺手返回添加顶点的数目
int AdjMatrixUndirNetwork::GetElem(int vex, char& data)
{
if (vex < 0 && vex >= vexNum)
return 0;
data = vertexes[vex];
return 1;
}
//顶点的数目
int AdjMatrixUndirNetwork::GetVexNum()
{
return vexNum;
}
//边的数目
int AdjMatrixUndirNetwork::GetArcNum()
{
return arcNum;
}
//返回顶点
char AdjMatrixUndirNetwork::GetElem(int vex)
{
return vertexes[vex];
}
//获得点位置在vex的第一条边
int AdjMatrixUndirNetwork::FirstAdjVex(int vex)
{
for (int i = 0; i < vexNum; i++)
if (arcs[vex][i] != infinity)
return i;
return -1;
}
//获取两个点之间的边
int AdjMatrixUndirNetwork::NextAdjVex(int vex, int vex2)
{
for (int i = vex2 + 1; i < vexNum; i++)
if (arcs[vex][i] != infinity)
return i;
return -1;
}
//返回权值
int AdjMatrixUndirNetwork::GetWeight(int vex1, int vex2)
{
return arcs[vex1][vex2];
}
//返回无限,初始化工作
int AdjMatrixUndirNetwork::GetInfinity()
{
return infinity;
}
//度的计算,度 = 出度 + 入度 = 邻接矩阵上该点的纵向+邻接矩阵上该点的横向
int AdjMatrixUndirNetwork::GetDegree(int vex)
{
int inDegree = 0; //入度
int outDegree = 0; //出度
int degree = 0; //度
for (int i = 0; i < vexNum; i++) {
inDegree += edges[i][vex];
outDegree += edges[vex][i];
}
degree = inDegree + outDegree;
return degree;
}
//返回点的状态
VisitStatus AdjMatrixUndirNetwork::GetTag(int vex)
{
return tag[vex];
}
//修改点的状态
int AdjMatrixUndirNetwork::SetTag(int vex, VisitStatus _tag)
{
if (vex >= vexNum)
return 0;
tag[vex] = _tag;
return 1;
}
//深度优先搜索
void AdjMatrixUndirNetwork::dfsTraverse()
{
for (int i = 0; i < vexNum; i++) { //首先将所有节点的状态设置为UNVISIT
tag[i] = UNVISIT;
}
for (int i = 0; i < vexNum; i++) { //然后对每一个点进行遍历
if (tag[i] == UNVISIT) { //如果这个点的状态是没有探寻过,直接深度优先搜索
DFS(i);
}
}
}
//深度优先搜索的回溯部分
void AdjMatrixUndirNetwork::DFS(int startVex)
{
cout << vertexes[startVex]<<endl; //输出当前节点的
SetTag(startVex, VISIT); //然后将其设置为以及探索
for (int j = 0; j < vexNum; j++) {
if (arcs[startVex][j] != 0 && arcs[startVex][j] != infinity && GetTag(j) == UNVISIT) {
DFS(j); //头铁撞墙的过程
}
}
}
//广度优先搜索
void AdjMatrixUndirNetwork::BFS()
{
queue<int> myqueue; //队列,用来存储当前层没有探索节点
for (int i = 0; i < vexNum; i++) { //将每一个节点都设置为没有探索过
tag[i] = UNVISIT;
}
for (int i = 0; i < vexNum; i++) {
if (tag[i] == UNVISIT) { //从该节点开始探索
tag[i] = VISIT; //将节点的状态设置为访问
cout << vertexes[i] << endl;
myqueue.push(i); //在该层删除i
while (!myqueue.empty()) { //队列为空意味着这一层搜索网
i = myqueue.front();
myqueue.pop(); //删除尾部元素
for (int j = 0; j < vexNum; j++) { //进行检验改变状态
if (tag[j] == UNVISIT && arcs[i][j] != infinity) {
tag[i] = VISIT;
cout << vertexes[j] << endl; //输出该层顶点
myqueue.push(j);
}
}
}
}
}
}
/*
Dijkstra算法采用的是一种贪心的策略,声明一个数组dis来保存源点到各个顶点的最短距离和一个保存已经找到了最短路径的顶点的集合:T,初始时,原点 s 的路径权重被赋为 0 (dis[s] = 0)。若对于顶点 s 存在能直接到达的边(s,m),则把dis[m]设为w(s, m),同时把所有其他(s不能直接到达的)顶点的路径长度设为无穷大。初始时,集合T只有顶点s。
然后,从dis数组选择最小值,则该值就是源点s到该值对应的顶点的最短路径,并且把该点加入到T中,OK,此时完成一个顶点,
然后,我们需要看看新加入的顶点是否可以到达其他顶点并且看看通过该顶点到达其他点的路径长度是否比源点直接到达短,如果是,那么就替换这些顶点在dis中的值。
然后,又从dis中找出最小值,重复上述动作,直到T中包含了图的所有顶点。
*/
void AdjMatrixUndirNetwork::Dijkstra(int startVex)
{
int vexNum = GetVexNum(), * dist, * path; //dist保存结果,path进行路径探索
int i, j, infinity = GetInfinity(), min;
int minOrder = 0;
dist = new int[vexNum];
path = new int[vexNum];
SetTag(startVex, VISIT);
for (i = 0; i < vexNum; i++) //初始化
{
if (i != startVex)
{
dist[i] = GetWeight(startVex, i);
if (dist[i] == infinity)
path[i] = -1;
else
path[i] = startVex;
}
else
{
dist[i] = 0;
path[i] = -1;
}
}
for (i = 1; i < vexNum; i++) //循环n-1次,找出以startvex为起点,其他n-1个顶点为终点的最短路径
{
min = infinity;
for (j = 0; j < vexNum; j++)
{
if (GetTag(j) == UNVISIT && dist[j] < min)
{
min = dist[j];
minOrder = j;
}
}
SetTag(minOrder, VISIT);
for (j = 0; j < vexNum; j++)
{
if (GetTag(j) == UNVISIT && (min + GetWeight(minOrder, j) < dist[j]))
{
dist[j] = min + GetWeight(minOrder, j);
path[j] = minOrder;
}
}
}
for (i = 0; i < vexNum; i++)
cout << dist[i] << " ";
cout << endl;
for (i = 0; i < vexNum; i++)
cout << path[i] << " ";
cout << endl;
for (i = 0; i < vexNum; i++)
{
if (i != startVex)
{
cout << "从起点" << GetElem(startVex) << "到终点" << GetElem(i) << "的最短路径长度为:" << dist[i];
cout << " 最短路径为:" << GetElem(i);
j = i;
while (path[j] != -1)
{
j = path[j];
cout << "<-" << GetElem(j);
}
cout << endl;
}
}
delete[] dist;
delete[] path;
}
/**
判断是否连通,这里采用了深度优先搜索的变形,如果在深度或者广度优先搜索之后
还存在图中的某一个节点的探索状态依旧为UNVISIT,那么表示该节点不连通,这里用了深度优先搜索
往死里撞南墙的特性
当然啦,如果是求强连通的数量,肯定适用tarjan算法,但是没必要搞这么复杂,把BFS变一下就算了
**/
//判断是否为连通图
bool AdjMatrixUndirNetwork::isConnected()
{
queue<int> myqueue; //队列,用来存储当前层的节点
for (int i = 0; i < vexNum; i++) { //将每一个节点都设置为没有探索过
tag[i] = UNVISIT;
}
for (int i = 0; i < vexNum; i++) {
if (tag[i] == UNVISIT) {
tag[i] = VISIT;
myqueue.push(i);
while (!myqueue.empty()) {
i = myqueue.front();
myqueue.pop();
for (int j = 0; j < vexNum; j++) {
if (tag[j] == UNVISIT && arcs[i][j] != infinity) {
tag[i] = VISIT;
myqueue.push(j);
}
}
}
}
}
for (int i = 0; i < vexNum; i++) {
if (tag[i] == UNVISIT) {
return false;
}
}
return true;
}
//检查是否为零图
bool AdjMatrixUndirNetwork::isEmpty()
{
if (arcNum == 0 || vexMaxNum == 0) { //如果边数和顶点数同时为零,那么就为零表
return true;
}
else {
return false;
}
}
/**
完全图的定义:
每个点之间恰好有一个直线相互连接,也就意味着边数和顶点数的数学关系式为:
network.vexNum * (network.vexNum - 1) / 2)
等于就是完全图,不等于就不是完全图
**/
bool AdjMatrixUndirNetwork::isComplete()
{
if (arcNum == (vexNum * (vexNum - 1) / 2)) {
return true;
}
else {
return false;
}
}
/**
只要满足公式network.arcNum <= (3 * network.vexNum - 6),就可以验证他是否是平面图
**/
bool AdjMatrixUndirNetwork::isPlane()
{
if (arcNum <= (3 * vexNum - 6)) {
return true;
}
else {
return false;
}
}
/**
对偶图中的每一个点即为平面图中的某一个面,对偶图中任意两点间的线都是平面图中对应两平面公共边的割线,
如果平面图中某一条边只属于一个面,那么在对偶图中就是一个环边
对偶图的边数等于平面图的边数,对偶图的点数等于平面图的面数
**/
void AdjMatrixUndirNetwork::transferDual()
{
if (isPlane() == false) {
cout << "非平面图没有对偶图" << endl;
return ;
}
AdjMatrixUndirNetwork dual(vertexes,vexNum);
dual.vexNum = (arcNum + 2 - vexNum);
for (int i = 0; i < vexNum; i++) {
for (int j = 0; j < vexNum; j++) {
int tmp = edges[i][j];
if (tmp == 0) {
dual.edges[i][j] = 1;
}
else {
dual.edges[i][j] = 0;
}
}
}
cout << "顶点图" << endl;
for (int i = 0; i < vexNum; i++)
{
cout << "[ ";
for (int j = 0; j < vexNum; j++)
cout << dual.edges[i][j] << " ";
cout << "]" << endl;
}
}
MinHeap.h
/**
MinHeap.h
该文章的原创作者:阿伟加油鸭。首发于CSDN平台,装载请标注博文出处。
网址:
**/
//最小生成堆用于kruskal算法中的抽取操作
#ifndef MIN_HEAP_H
#define MIN_HEAP_H
#include MinSpanTreeKruskal.h
/**
文件名:MinSpanTreeKruskal.h
该文章的原创作者:阿伟加油鸭。首发于CSDN平台,装载请标注博文出处。
网址:
**/
//最小生成树,Kruskal算法
#ifndef MINSPANTREE_KRUSKAL_H
#define MINSPANTREE_KRUSKAL_H
#include "AdjMatrixUndirNetWork.h"
#include "UFSets.h"
#include "MinHeap.h"
#include MinSpanTreePrim.h
/**
文件名:MinSpanTreePrim.h
该文章的原创作者:阿伟加油鸭。首发于CSDN平台,装载请标注博文出处。
网址:
**/
//Prim算法
/*
1. 在一个加权连通图中,顶点集合V,边集合为E
2. 任意选出一个点作为初始顶点,标记为visit,计算所有与之相连接的点的距离,选择距离最短的,标记visit.
3. 重复以下操作,直到所有点都被标记为visit:
在剩下的点钟,计算与已标记visit点距离最小的点,标记visit,证明加入了最小生成树。
*/
#ifndef MINSPRNTREE_PRIM_H
#define MINSPRNTREE_PRIM_H
#include UFSets.h
/**
文件名:UFSets.h
该文章的原创作者:阿伟加油鸭。首发于CSDN平台,装载请标注博文出处。
网址:
**/
//堆,有合并操作,用于Kruskal算法
#ifndef UFSETS_H
#define UFSETS_H
#include 测试用例以及主函数:main.cpp
/**
文件名:main.cpp
该文章的原创作者:阿伟加油鸭。首发于CSDN平台,装载请标注博文出处。
网址:
**/
/**
顶点表
[A B C D E F]
测试的图:
权重图: 邻接矩阵
A B C D E F A B C D E F
A [500 34 46 500 500 19 ] A [ 0 1 1 0 0 1 ]
B [34 500 500 500 12 500 ] B [ 1 0 0 0 1 0 ]
C [46 500 500 17 500 25 ] C [ 1 0 0 1 0 1 ]
D [500 500 17 500 38 25 ] D [ 0 0 1 0 1 1 ]
E [500 12 500 38 500 26 ] E [ 0 1 0 1 0 1 ]
F [19 500 25 25 26 500 ] F [ 1 0 1 1 1 0 ]
图的连接关系: 图的结构:以A为上
A: B C F A
B: A E / | \
C: A D F / | \
D: C E F B F - C
E: B D F | / \ |
F: A C D E | / \ |
E - - - D
预期结果:
顶点C的度 6
是否为连通图 0 不是
是否为平面图 1 是
是否为完全图 0 不是
是否为零图 0 不是
对偶图转化(这里只显示邻接矩阵)
[ 1 0 0 1 1 0 ]
[ 0 1 1 1 0 1 ]
[ 0 1 1 0 1 0 ]
[ 1 1 0 1 0 0 ]
[ 1 0 1 0 1 0 ]
[ 0 1 0 0 0 1 ]
Prim算法:
连接边: (A,F),权:19
连接边: (F,C),权:25
连接边: (C,D),权:17
连接边: (F,E),权:26
连接边: (E,B),权:12
最小生成树生成成功
Kruskal算法:
连接边: (B,E),权:12
连接边: (C,D),权:17
连接边: (A,F),权:19
连接边: (D,F),权:25
连接边: (E,F),权:26
最小生成树生成成功
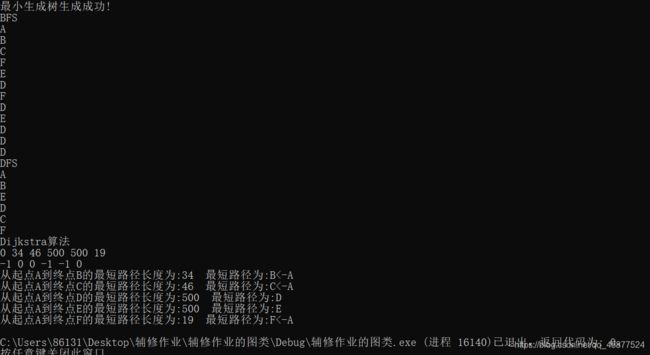
BFS:A B C F E D F D E D D D
DFS: A B E D C F
Dijkstra算法
0 34 46 500 500 19
-1 0 0 -1 -1 0
从起点A到终点B的最短路径长度为:34 最短路径:B<-A
从起点A到终点C的最短路径长度为:46 最短路径:C<-A
从起点A到终点D的最短路径长度为:500 最短路径:D
从起点A到终点E的最短路径长度为:500 最短路径:E
从起点A到终点F的最短路径长度为:19 最短路径:F<-A
**/
#include "MinSpanTreeKruskal.h"
#include "MinSpanTreePrim.h"
using namespace std;
int main()
{
char vexs[7] = "ABCDEF";
AdjMatrixUndirNetwork network(vexs, 6);
network.InsertArc(0, 1, 34);
network.InsertArc(0, 2, 46);
network.InsertArc(0, 5, 19);
network.InsertArc(2, 5, 25);
network.InsertArc(1, 4, 12);
network.InsertArc(5, 4, 26);
network.InsertArc(5, 3, 25);
network.InsertArc(2, 3, 17);
network.InsertArc(3, 4, 38);
network.Display(); //展示图
cout << endl;
cout << "顶点的度:" << network.GetDegree(2) << endl; //顶点的度
cout << "判断是否为连通图" << network.isConnected() << endl; //判断是否为连通图
cout << "判断是否为平面图" << network.isPlane() << endl; //判断是否为平面图
cout << "判断是否为完全图" << network.isComplete() << endl; //判断是否为完全图
cout << "判断是否为零图" << network.isEmpty() << endl; //判断是否为零图
cout << "对偶图转化" << endl;
network.transferDual(); //对偶图转化
cout << "Prim算法" << endl;
MinSpanTreePrim(network); //Prim算法
cout << "Kruskal算法" << endl;
MinSpanTreeKruskal(network); //Kruskal算法
cout << "BFS" << endl;
network.BFS(); //广度优先搜索
cout << "DFS" << endl;
network.dfsTraverse(); //深度优先搜索
cout << "Dijkstra算法" << endl;
network.Dijkstra(0); //Dijkstra算法
return 0;
}