为什么PPIO作为去中心化存储,也能像阿里云、AWS S3一样,保证数据不丢失?
在去中心化存储这个概念被提及之后,很多人都担心去中心化存储的数据丢失问题。
他们认为:当我在去中心存储里面存放了数据之后,虽然它有更便宜,更快,更隐私等特点,但是数据毕竟存在于矿工的矿机上,由于矿工的不稳定性,可能导致文件的丢失。就像滴滴的司机一样,大部分时间是靠谱的,偶尔不靠谱,不靠谱的时候,体验非常差,这样的产品怎么能让人放心使用呢。
另一方面,反观大公司提供的存储服务,比如:亚马逊AWS S3是专业机房,专业机器,专业硬盘,能保证数据不丢失。
其实不是这样的,总架构师在设计PPIO的时候,早就考虑到这个问题,这篇文章就来解释下大家的疑惑。
首先,需要纠正几个认知误区:
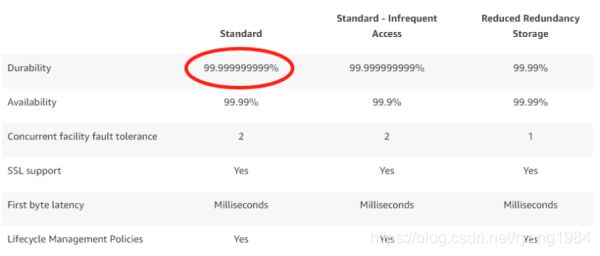
- AWS S3等大公司能 100 100% 100保证存储文件不丢失吗?
其实是不能的,他们只能 99.999999999 99.999999999% 99.999999999保证存储文件不丢,专业术语称为: 11 个 9 11个9 11个9的保证存储文件不丢。存储行业称 99.999999999 99.999999999% 99.999999999这个服务质量指标(QoS)为耐用率。
- 矿工可能不稳定。
P2P(点对点)的技术核心,就是在多个不稳定的节点上,实现稳定的服务。熟悉PPTV的朋友应该知道,使用的就是P2P直播,正是在多个不稳定的节点上完成了稳定的服务。
下面来详细解释:为何PPIO也能像大型公司一样靠谱,以及是如何把这个耐用率(QoS)做到像大型公司一样高的。
PPIO的2种冗余模式
总架构师在设计PPIO的时候,设计了2种冗余模式:
全副本模式
全副本模式就是把文件,完整地拷贝,新文件和老文件一模一样,这样做并不节约空间,但是P2P能多点下载数据,速度更快,同时可以保证用户下载体验。
纠删副本模式
纠删副本模式就是通过纠删技术来做冗余。简单地说就是,数据分成碎片并编码,使用可配置数量的冗余分片,将所有文件分片存储在不同矿工上。这样做虽然不利于P2P多点传输,但是可以大大节约冗余空间。
PPIO就是通过将以上两种方式进行结合,以应对不同使用场景。
下面简单说一下纠删技术产生的数学特征:
不妨用 ( k , n ) (k,n) (k,n) 纠删码来编码数据,其中:
n n n表示总共有 n n n个纠删片段
k k k表示在 n n n个纠删片段中,任何 k k k个纠删片段就能完全恢复原始数据。
如果数据大小是 s s s字节,则每个纠删片段的大小大约是 s / k s/k s/k 字节。
如果 k = 1 k = 1 k=1时,就相当于复制一个全副本。
例如,1MB数据, 如果采用(10,16)纠删码,并且每个纠删片段大小是0.1M,则总存储数据大小就是1.6M。它实际总共用了1.6倍的数据空间大小。
PPIO的假设和计算
做如下假设:
令t为单位假设时间,这里先假设 t = 24 小 时 t=24小时 t=24小时
P t Pt Pt代表矿工的日掉线率,这里假设 P t = 5 Pt=5% Pt=5
τ为副本丢失后的修复时间,也就是如果副本丢失了,多少时间能够修复。假设 τ = 2 小 时 τ=2小时 τ=2小时。
在可以修复的前提下,将以上数值带入下面的公式,算得单副本丢失每天丢失的概率是:
p = 1 – ( 1 − P t ) t τ = 0.4265318778 p = 1 – (1-Pt)^{\frac{t}{τ}} = 0.4265318778% p=1–(1−Pt)τt=0.4265318778
PPIO设计的默认全副本数冗余是2倍,纠删副本冗余是1.5倍。
下面来看全副本模式
由于全副本是完全复制,也就是2倍的冗余,即有2个副本,称为 N = 2 N=2 N=2。
修复时间内的耐用率:
P a = 1 − p 2 = 99.9981807056 P_a = 1- p^2 = 99.9981807056% Pa=1−p2=99.9981807056
全年耐用率:
P y a = P a ( 365 ∗ t / τ ) = 92.3406415922 P_{ya} = Pa^{(365*t/τ)} = 92.3406415922% Pya=Pa(365∗t/τ)=92.3406415922
再看纠删模式
假设采用的纠删算法是 ( k , n ) = ( 6 , 9 ) (k,n)= (6,9) (k,n)=(6,9)。
相当于6M的数据,每个纠删分片是1M,一共要存放9个纠删分片,任意6个分片就能恢复出完整的数据,这样存放在9个矿工上,另外实际占用的空间大小是9M。
如果理解了,继续往下看。
由于纠删算法是(k,n), 那么冗余就是 F = n / k = 1.5 F = n/k = 1.5 F=n/k=1.5。
在修复时间内分片丢失数就是: m = n ∗ p = 0.038387869 m = n*p = 0.038387869 m=n∗p=0.038387869,这是已知发生数。
这里讲解一下概率论中的经典公式,泊松分布拟合公式:
P ( x ) = m x x ! e − m P(x) = \frac{m^x}{x!}e^{-m} P(x)=x!mxe−m
简单理解一下,泊松分布拟合公式就是观察事物平均发生 m m m次的条件下,实际发生 x x x次的概率。要了解推导细节,可以看最后的附录。
套用泊松分布拟合公式就可以得到:
P b = ∑ i = 0 n − k P ( i ) Pb=\sum_{i=0}^{n-k}P\left(i\right) Pb=i=0∑n−kP(i)
即 P b = 99.9999912252 P_b = 99.9999912252% Pb=99.9999912252
那么全年的耐用率: P y b = P b ( 365 t τ ) = 99.9615738663 P_{yb} = Pb^{(365\frac{t}{τ})} = 99.9615738663% Pyb=Pb(365τt)=99.9615738663
可以看到,虽然冗余更小,但纠删模式比全副本模式的耐用率(QoS)要高很多。
计算汇总
把2种冗余模式结合起来,可以得到最终的耐用率:
修复时间内耐用率: P = 1 – ( 1 − P a ) ( 1 − P b ) = 99.9999999998 P = 1 – (1-Pa)(1-Pb) = 99.9999999998% P=1–(1−Pa)(1−Pb)=99.9999999998
全年耐用率: P y = P ( 365 t τ ) = 99.9999993008 P_y = P^{(365\frac{t}{τ})} = 99.9999993008% Py=P(365τt)=99.9999993008
可以看到,已经达到8个9的耐用率。也就是说:假设你存放了1亿个文件,一年只会丢失1个文件。
还能提高
上面的假设,是基于 ( k , n ) = ( 6 , 9 ) (k,n)= (6,9) (k,n)=(6,9), 冗余度为 F = 1.5 F=1.5 F=1.5计算出来的。
如果适当提高冗余度 F F F,或者提高 k k k,还能进一步提高全年的耐用率 P y Py Py。
下面的这个表格就是调整 k k k和 F F F之后对全年耐用率产生的影响。我们这里做了一个新的假设,没有全副本,只有纠删分片。
这样做,不追求速度,只追求价格最便宜。这时候, P y Py Py 就等于 P y b Pyb Pyb。即:

可以看出,冗余度 F F F越高,耐用率越高。同时, 分片数 n n n越多,耐用率越高。 n n n对耐用度的影响更为敏感,但是 n n n越大,也就意味这需要的矿工越多。
也可以看出,如果要追求12个9(和大型公司同样服务水平),即99.9999999999。采用纠删模式,在冗余度2的情况下,分成16个纠删副本就能做到;同样,在冗余度2.5的情况下,分成12个纠删副本就能做到。这样就超过 AWS S3企业级存储服务的年耐用率(11个9)。
还能再提高
除了调整 N N N, ( k , n ) (k,n) (k,n), F F F 这些参数可以提高耐用率之外,还可以通过自身的优化努力。其实还有很大的提升空间,前面说过,这个测算是基于2个前提假设的。而这两个假设本身还有很大的提升空间。
单副本的每日丢失率Pt, 计算时假设是5%。这个假设本身是可以通过token经济系统的设计来降低的。更合理的经济系统可以提高矿工的稳定性和在线率。如果矿工稳定了,这个值就会下降;这个值越低,全年的耐用率就会增加。这个值有望降至1%甚至更低。
副本丢失后的修复时间 τ,计算时假设是2小时。这个假设也可以通过PPIO自身的算法来优化,只要能更快地发现副本丢失,能更快地增加副本数来保证副本数充足,τ值就会越低;τ值越低,全年的耐用率就会增加。如果算法做到极致的话,这个值有望降至15分钟。
假设做到了极限值 P t = 1 Pt=1% Pt=1, τ = 0.25 τ=0.25 τ=0.25小时, ( k , n ) = ( 6 , 9 ) (k,n)=(6,9) (k,n)=(6,9),纠删副本冗余度 F = 1.5 F=1.5 F=1.5。
得到 P y b = 99.9999998852 P_{yb} = 99.9999998852% Pyb=99.9999998852
如果再考虑2个全副本冗余,则全年耐用率:
P y = 99.9999999999 P_y = 99.9999999999% Py=99.9999999999
对于其他去中心化存储项目,如Filecoin,Storj等,虽然公开的细节不多,但是也可以使用类似的方式进行测算。
让开发者灵活设置参数
总架构师在设计PPIO架构的时候,给予开发者足够的灵活性,可以根据自身的情况设置不同的参数,其中包括:全副本数 N, 纠删算法参数 (k,N)。
开发者可以根据自身的需求,如传输速度,价格(冗余度越高,价格越高),能接受的耐用率来配置参数,从而满足自己的产品要求。
附录:泊松分布拟合公式推导
假设 p p p 为单个设备单位时间内的故障率,则 n n n 个设备在单位时间内,有 k k k 个设备发生故障的概率 P ( k ) P(k) P(k) 为:
P ( k ) = ( n k ) p k ( 1 − p ) n − k P(k) = {n \choose k}p^{k}(1-p)^{n-k} P(k)=(kn)pk(1−p)n−k
展开组合:
P ( k ) = n ( n − 1 ) ⋯ ( n − k + 1 ) k ! p k ( 1 − p ) n − k P(k) = \frac{n(n-1)\cdots(n-k+1)}{k!}p^{k}(1-p)^{n-k} P(k)=k!n(n−1)⋯(n−k+1)pk(1−p)n−k
P ( k ) = n ( n − 1 ) ⋯ ( n − k + 1 ) k ! p k ( 1 − p ) n ( 1 − p ) k P(k) = \frac{n(n-1)\cdots(n-k+1)}{k!}\frac{p^{k}(1-p)^{n}}{(1-p)^{k}} P(k)=k!n(n−1)⋯(n−k+1)(1−p)kpk(1−p)n
P ( k ) = ( n p ) ( n p − p ) ⋯ ( n p − k p + p ) k ! ( 1 − p ) 1 p n p ( 1 − p ) k P(k) = \frac{(np)(np-p)\cdots(np-kp+p)}{k!}\frac{(1-p)^{ \frac{1}{p} {np}}}{(1-p)^{k}} P(k)=k!(np)(np−p)⋯(np−kp+p)(1−p)k(1−p)p1np
假设 p p p 很小, n n n 很大,一般地当 n > 20 n > 20 n>20, p < 0.05 p < 0.05 p<0.05 时。
∵ lim p → 0 ( 1 − p ) − 1 p → e \because \lim \limits_{p \to 0} (1-p)^{-\frac{1}{p}} \to e ∵p→0lim(1−p)−p1→e
n → + ∞ , p → 0 n \to +\infty, p \to 0 n→+∞,p→0
∴ P ( k ) ≈ ( n p ) ( n p − p ) ⋯ ( n p − k p + p ) k ! e − n p ( 1 ) k \therefore P(k) \approx \frac{(np)(np-p)\cdots(np-kp+p)}{k!}\frac{e^{-{np}}}{(1)^{k}} ∴P(k)≈k!(np)(np−p)⋯(np−kp+p)(1)ke−np
P ( k ) ≈ ( n p ) k k ! e − n p P(k) \approx \frac{(np)^k}{k!}e^{-{np}} P(k)≈k!(np)ke−np
令
L a t e x : λ = n p Latex: \lambda = np Latex:λ=np
最后得到泊松分布公式,即,已知单位时间内平均有 λ \lambda λ 个设备故障,计算单位时间内有 k k k个设备故障的概率。
L a t e x : P ( k ) = λ k k ! e − λ Latex: P(k) = \frac{\lambda^k}{k!}e^{-\lambda} Latex:P(k)=k!λke−λ
参考:
1.ttps://www.scality.com/blog/durability-availability-managing-fragile-scarce/
2.Hakim Weatherspoon and John D. Kubiatowicz, Erasure Coding vs. Replication: A Quantitative Comparison.
3.Byung-Gon Chun, Frank Dabek, Andreas Haeberlen, Emil Sit, Hakim Weatherspoon, M. Frans Kaashoek, John Kubiatowicz, and Robert Morris, Efficient Replica Maintenance for Distributed Storage Systems.
想了解更多有关PPIO的信息,可以移步官网:PPIO