【译】SNARKs讲解「第七部分」:椭圆曲线的配对
原文链接
<<< 第六部分
在第六部分,我们看到皮诺曹zk-SNARK的一个轮廓。我们还差2样东西:一个支持加法和乘法的HH,它在验证者检查的时候会用到 ;另一个是从交互协议到非交互证明系统的转换。
在本文中我们将看到使用椭圆曲线,让我们可以获得一个受限的,但足够好的一种支持乘法的HH。我们随后将展示这个受限的HH同样也足够用来把我们的协议转换成我们希望的非交互系统。
我们首先介绍一下椭圆曲线,并且解释一下它们如何能给到我们需要的HH。
椭圆曲线和他们的配对
假定 p p p 是一个大于3的质数,找一些 u , v ∈ F p u,v \in \textbf F_p u,v∈Fp,使得 4 u 3 + 27 v 2 ≠ 0 4u^3+27v^2 \, \neq 0 4u3+27v2̸=0。然后考察这个方程
Y 2 = X 3 + u ⋅ X + v Y^2=X^3+u \cdot X + v Y2=X3+u⋅X+v
一个椭圆曲线 C C C 是一个满足这个方程的点 ( x , y ) (x,y) (x,y) 1的集合。这些曲线给我们一个有趣的方法来构造群。群元素是在曲线上的点 ( x , y ) ∈ F p 2 (x,y) \in \textbf F_p^2 (x,y)∈Fp2,也就是,这个群包括满足方程的点和一个特殊点 O O O。
由于技术原因这个特殊点有时也被称作“无限点”,起到恒等元素的作用,也就是群里的零。
现在,问题是我们如何把2个点 P = ( x 1 , y 1 ) , Q = ( x 2 , y 2 ) P=(x_1,y_1),Q=(x_2,y_2) P=(x1,y1),Q=(x2,y2) 相加,得到第3个点?加法规则是从曲线的叫做因子类群的抽象对象派生出来的。对于我们的目的,你所需要知道关于因子类群的所有信息就是它在 加法定义上施加下面这个限制:在任意线上点的合必须为零,也就是, O O O。
让我们看一下这个加法规则是如何从这个限制派生出来的。让我们看一下由形式为 X = c X=c X=c 的方程定义的竖直线。假定这条线跟曲线在点 P = ( x 1 , y 1 ) P=(x_1,y_1) P=(x1,y1) 处相交。因为这条曲线是 Y 2 = f ( X ) Y^2=f(X) Y2=f(X),如果 ( x 1 , y 1 ) (x_1,y_1) (x1,y1) 在曲线上,那么点 Q : = ( x 1 , − y 1 ) Q:=(x_1,-y_1) Q:=(x1,−y1) 也在。进一步,由于这是条竖线并且曲线方程在 Y Y Y上是2阶的,我们可以确定这2个点就是这条竖线跟曲线相交的全部点。
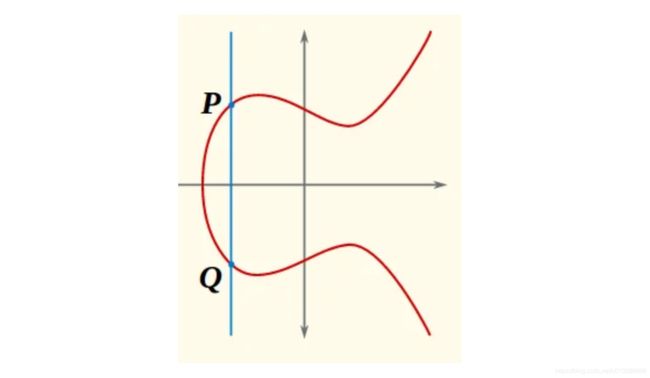
于是必须有 P + Q = O P+Q=O P+Q=O,这意味着 P = − Q P=-Q P=−Q, 也就是, Q Q Q 是 P P P 在群里的相反数。
现在让我们看一下具有不同第一坐标的点P和Q,既 x 1 ≠ x 2 x_1 \;\;\neq x_2 x1̸=x2,然后看一下如何把它们加起来。我们做一条直线穿过P和Q。
由于这条曲线是由X阶数为3的多项式定义的,并且已经跟这条非竖直线相交于2点,那么它一定会跟这条 直线相交于第3点(用 R = ( x , y ) R=(x,y) R=(x,y)表示),而再没有其他点。
以此我们必须有 P + Q + R = O P+Q+R=O P+Q+R=O,也就是 P + Q = − R P+Q=-R P+Q=−R; 而且我们现在知道 − R -R −R 可以用翻转第二个坐标的方法从 R R R 得到。
于是我们得到了我们群的加法规则:给定点P和Q,做一条直线穿过它们,然后取第3个交点的 “镜像”点作为加法的结果。2
这个群通常被称作 C ( F p ) C(F_p) C(Fp),这是因为它由坐标在 F p F_p Fp 中的曲线 C C C 上的点组成;不过让我们从现在开始用 G 1 G_1 G1 来表示。为了简单,我们假设 G 1 G_1 G1 中元素的个数为一个质数 r r r,并且不同于 p p p。 这是很常见的情况,例如,在Zcash目前正在使用的曲线里。在这个情况下,任何不是 O O O 的元素 g ∈ G 1 g \in G_1 g∈G1 都生成 G 1 G_1 G1。(译者:也就是说这些任意 g g g 都是群 G 1 G_1 G1的生成器)
使得 p k − 1 p^k-1 pk−1 被 r r r 整除的最小的整数 k k k 被称作曲线的嵌入阶。据推测当 k k k 不太小的时候,比如,至少是6,那么 G 1 G1 G1 里的离散对数问题会非常难(在Zcash当前使用的BN曲线3中 , k = 12 k=12 k=12)。
乘法群 F p k \textbf F_p^k Fpk 包含一个我们表示为 G T G_T GT的 r r r 阶子群。我们可以看一下那些坐标不仅在 F p \textbf F_p Fp 上,还可能在 F p k \textbf F_p^k Fpk 上的曲线上面的点。在相同的加法规则上,这些点和 O O O 一起也形成一个群。注意 C ( F p k ) C(\textbf F_p^k) C(Fpk) 清楚地包含 G 1 G_1 G1。除开 G 1 G1 G1, C ( F p k ) C(\textbf F_p^k) C(Fpk) 将包含一个额外的 r r r 阶(实际上, r − 1 r-1 r−1 个阶数为 r r r 的子群)子群 G 2 G_2 G2。
固定住发生器 g ∈ G 1 , h ∈ G 2 g \in G_1, h \in G_2 g∈G1,h∈G2。结果是我们有一个高效的映射。这个映射被称作Tate缩减配对。它把一对G1和G2中的元素映射到 G T G_T GT中的元素,使得
- 对一个 G T G_T GT的发生器 g \textbf g g,有 T a t e ( g ⋅ h ) = g Tate(g\cdot h)=\textbf g Tate(g⋅h)=g。
- 给定一对 元素 a , b ∈ F r a,b\in \textbf F_r a,b∈Fr,我们有 T a t e ( a ⋅ g , b ⋅ h ) = g a b Tate(a \cdot g,b \cdot h)=\textbf g ^{ab} Tate(a⋅g,b⋅h)=gab。
定义Tate有一点超出本系列文章范围,它是基于代数几何 的概念,特别是基于其中的因子的概念。这里是一个Tate定义的 草案:4
对于 a ∈ F p a \in F_p a∈Fp,多项式 ( X − a ) r (X-a)^r (X−a)r 在点 a a a 上为 r r r次零,在其他点上不等于零。对于一个点 P ∈ G 1 P \in G_1 P∈G1, 因子使得我们能够证明存在一个函数 f p f_p fp,它从曲线映射到 F p F_p Fp。在某个准确的理解上,这在 P P P点上有 r r r 次零,再无其他零。 T a t e ( P , Q ) Tate(P,Q) Tate(P,Q)于是 被定义成 f P ( Q ) ( p k − 1 ) / r f_P(Q)^{(p^k-1)/r} fP(Q)(pk−1)/r。
也许,看起来这个定义如何跟声明的特性有关并不是很清晰,实际上证明Tate有这些特性是相当复杂的。
定义 E 1 ( x ) : = x ⋅ g , E 2 ( x ) : = x ⋅ h , E ( x ) : = x ⋅ g E_1(x):=x⋅g,E_2(x):=x⋅h,E(x):=x⋅g E1(x):=x⋅g,E2(x):=x⋅h,E(x):=x⋅g,我们得到一个支持加法和乘法的HH的弱版本: E 1 , E 2 , E E_1,E_2,E E1,E2,E 是支持加法的HH,而且给定隐藏 E 1 ( x ) , E 2 ( y ) E_1(x),E_2(y) E1(x),E2(y),我们可以计算 E ( x y ) E(xy) E(xy)。换句话说,如果我们有 x x x 和 y y y 的正确的隐藏,我们可以得到一个(不同的 ) x y xy xy 的隐藏。但是例如,如果我们有 x , y , z x,y,z x,y,z 的隐藏,我们无法得到 x y z xyz xyz的 隐藏 。
我们接下来讨论非交互证明系统。我们在开始的时候,解释一下到底“非交互”是什么意思。
共同参考串模型中的非交互证明
非交互最强最直观的表达也许就是如下。为了证明某一个声明,一个证明者广播一条消息给所有相关方,而且事先没有任何通信发生;任何读到这条消息的人都会相信证明者的声明。在多数场合下这看起来都不大可能。 5
非交互证明的一个稍微宽松些的表达是允许一个公共参考串(CRS)。在这个CRS模型里,在任何证明被构造之前,有一个设置阶段。在该阶段,我们根据某个随机过程,构造一个串,并且广播给所有相关方。这个串被称为CRS,然后被用来帮助构造和验证证明。这里的假设是任何人都不知道用来创建CRS的随机数,这是因为这个随机数可以被用来构造虚假声明的证明。
我们将解释在CRS模型里如何可以把第四部分里的可验证盲求值转化成一个非交互系统。由于第六部分里的协议由好几个这样的子协议组成,它可以用相似的办法转化成非交互证明。
一个非交互求值协议
求值协议的非交互版本基本就是把Bob的第一个消息当作CRS发布。回忆一下,这个协议的目的是去获得Alice在随机点 s ∈ F r s \in \textbf F_r s∈Fr 上的多项式 P P P 的隐藏 E ( P ( s ) ) E(P(s)) E(P(s))。
设置:选取随机数 α ∈ F r ∗ , s ∈ F r \alpha \in \textbf F_r^*, s \in \textbf F_r α∈Fr∗,s∈Fr,然后 发布CRS:
( E 1 ( 1 ) , E 1 ( s ) , … , E 1 ( s d ) , E 2 ( α ) , E 2 ( α s ) , … , E 2 ( α s d ) ) (E_1(1),E_1(s),…,E_1(s^d), E_2(α),E_2(αs),…,E_2(αs^d)) (E1(1),E1(s),…,E1(sd),E2(α),E2(αs),…,E2(αsd))
证明:Alice用CRS里的元素和 E 1 E_1 E1 和 E 2 E_2 E2 支持线性组合的事实,计算 a = E 1 ( P ( s ) ) a=E_1(P(s)) a=E1(P(s)) 和 b = E 2 ( α P ( S ) ) b=E_2(αP(S)) b=E2(αP(S)) 。
验证:固定 x , y ∈ F r x,y \in \textbf F_r x,y∈Fr 使得 a = E 1 ( x ) a=E_1(x) a=E1(x) 和 b = E 2 ( x ) b=E_2(x) b=E2(x)。Bob计算 E ( α x ) = T a t e ( E 1 ( x ) , E 2 ( α ) ) E(αx)=Tate(E_1(x),E_2(α)) E(αx)=Tate(E1(x),E2(α)) 和 E ( y ) = T a t e ( E 1 ( 1 ) , E 2 ( y ) ) E(y)=Tate(E_1(1),E_2(y)) E(y)=Tate(E1(1),E2(y)),并且检查是否它们相等(如果它们相等,就意味着 α x = y \alpha x = y αx=y)。
就像在第四部分解释的一样 ,Alice若要构造能通过验证检查的 a , b a,b a,b,那么 a a a必须是在 s s s点的d阶多项式 P ( s ) P(s) P(s) 的隐藏,其中 d d d 对她是已知的。这里主要的区别是Bob做验证检查时不需要知道 α \alpha α,因为他可以用配对函数来从 E 1 ( x ) E_1(x) E1(x) 和 E 2 ( α ) E_2(\alpha) E2(α) 中计算出 E ( α x ) E(\alpha x) E(αx)。
于是,他自己不需要构造并发送这第一个消息,这个消息可以在CRS里被很简单地修复。
你可以问“这个集合里的点是从哪里来?”。我们的意思是集合里的点的坐标在代数闭集 F p \textbf F_p Fp 上。同样这个曲线有一个仿射和投射版本 。当我们指投射版本时,我们把"无限点"O包含在曲线的元素 里。 ↩︎
我们没有解决P跟自己相加这个问题。如果要做的话 ,可以用曲线在P点的做切线,把R当作该切线与曲线的第二个交点。 ↩︎
https://eprint.iacr.org/2005/133.pdf ↩︎
Zcash真正在使用的配对是优化Ate配对,它是基于Tate缩减配对开发出来的,它的计算效率比Tate高不少。 ↩︎
在计算复杂性理论的术语里 ,只有BPP中的语言有非交互零知识证明。在Zcash交易中我们需要去证明的申明类型, 例如,“我知道一个串的哈希前像“,对应的复杂度类别为NP。人们相信NP问题比BPP问题的复杂度大很多。 ↩︎
