基于python实现通俗易懂讲解并查集

1. “并”的意思是把两个处在同一连通分量的节点给并到一起。
2. “查”的意思是查找一个节点的根节点，如果两个节点根节点相同，那他们就在同一连通分量中。
3. “并”的时候需要用到“查”，就是查找同一连通分量的节点。

并查集是一种树形的数据结构：

1.并查集用于判断一对元素是否相连，它们的关系是动态添加的，这一类问题叫做动态连通性问题。
2.主要支持合并和查询是否在同一个集合的操作。
3.底层结构是数组或者哈希表，用于表示结点指向的根结点。 4。合并就是把一个集合的根结点指向另一个集合的根结点，只要根结点一样，就表示在同一个集合中，也就是同一连通分量中。
5.这种·表示不相交集合的方法称之为代表元法，以每个结点的跟结点作为一个集合的代表元。

并查集的应用： 最小生成树：kruskal算法。

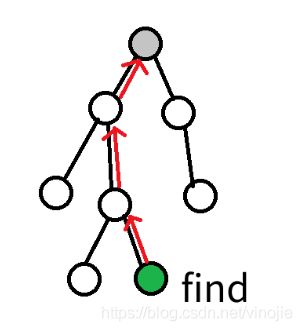
1、查找（查找一个结点的根结点）

建立一个parent数组，里面存放的是每个结点的根结点
初始化每个结点的根结点为本身 $parent[i]=i$.

parent数组的目的就是为了查找跟结点，根据这个数组，我们就可以找到每个结点的根结点。

代码实现：

for i in range(N):#假设有N个结点
    parent[i] = i #初始化每个结点的根结点是本身
def find(x, parent):
    r = x # 假设根就是当前的结点
    while r != parent[r]: # 如果假设不成立（r不是根节点），就继续循环
        r = parent[r] # 假设根节点是当前节点的父节点，即往树的上面走一层
    return r # 循环结束了，根也就找到了

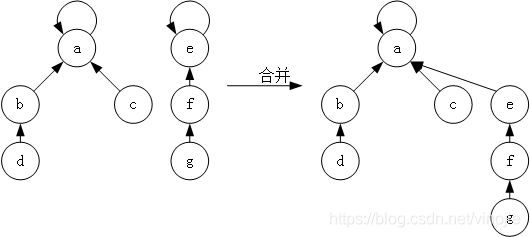
2、并（“并”的意思就是将根结点相同的结点合并到一起）

比如说 有两个结点$X$,$Y$，他们的根结点开始分别是$A$,$B$,但是根据某个条件，例如$X$,$Y$表示两个人，$A$,$B$表示他们的父亲，但是我们有个条件，$A$的父亲是$B$，也就是说$X$,$Y$的祖先都是$B$，那么我们将这两个结点合并到一起让他们的祖先都是$B$，怎么做呢，

代码如下：

if x 和 y 根据某个条件判断他们应该在一个集合中：
那么就将他们进行合并操作
def union(x, y, parent):
    x_root = find(x, parent)
    y_root = find(y, parent)
    # 将x作为根节点
    if x_root != y_root:
        parent[y_root] = x_root

3、leetcode例题：

3.1 等式方程的可满足性

题目描述：给定一个由表示变量之间关系的字符串方程组成的数组，每个字符串方程 equations[i] 的长度为 4，并采用两种不同的形式之一：“a==b” 或 “a!=b”。在这里，a 和 b 是小写字母（不一定不同），表示单字母变量名。

只有当可以将整数分配给变量名，以便满足所有给定的方程时才返回 true，否则返回 false。

输入：[“ab",“b!=c”,"ca”]
输出：false

基本思路：
我们可以将每一个变量看作图中的一个节点，把相等的关系 == 看作是连接两个节点的边，那么由于表示相等关系的等式方程具有传递性，即如果 ab 和 bc 成立，则 a==c 也成立。也就是说，所有相等的变量属于同一个连通分量。因此，我们可以使用并查集来维护这种连通分量的关系

首先初始化所有字母的根结点为本身，这里只有小写字母，因此我们创建26个字母的数组，parent[i]，i为对应字母的索引，例如：“a”对应1，“b”对应2，…

然后遍历所有等式，相等的等式中字母属于同一连通量，也就是根结点相同，对其进行合并操作。

然后遍历所有不等式，如果同一不等式字母的根结点相同，就说明前一步，这两个字母之间存在等式，它们处在同一连通分量中，产生矛盾，返回False。

如果遍历完所有的不等式没有发现矛盾，则返回 true。

代码实现：

class Solution:
    def equationsPossible(self, equations: List[str]) -> bool:
        parent = [i for i in range(26)] #初始化数组
        #定义查找根结点的函数
        def find(x):
            if x == parent[x]:
                return parent[x]
            else:
                while x!= parent[x]:
                    x = parent[x]
                return x
        
        for eq in equations:
            if eq[1] == "=":#满足这个条件说明它们应该在同一连通分量中，将其合并。
                r1 = find(ord(eq[0])-ord('a'))#查找根结点
                r2 = find(ord(eq[3])-ord('a'))
                if r1!=r2:#如果这两个结点根结点相同，说明不需要操作，否则就进行合并。
                    parent[r1]=r2
        
        for eq in equations:#再遍历不等式，如果它们跟结点相同则矛盾。
            if eq[1]=="!":
                r1 = find(ord(eq[0])-ord('a'))
                r2 = find(ord(eq[3])-ord('a'))
                if r1==r2:
                    return False
        return True

3.2 朋友圈

题目描述：班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。

给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果M[i][j] = 1，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。

输入:
[[1,1,0],
[1,1,0],
[0,0,1]]
输出: 2
说明：已知学生0和学生1互为朋友，他们在一个朋友圈。
第2个学生自己在一个朋友圈。所以返回2。

基本思路：与前一题类似，只不过这里需要计算的集合的数量，也就是我们将所有有朋友关系的人合并，然后看看合并后还有几个跟结点，一个跟结点代表一个朋友圈。

代码如下：

class Solution:
    def findCircleNum(self, M: List[List[int]]) -> int:
        parent = [i for i in range(len(M))]

        def find(x, parent):
            r  = x
            while r != parent[r]:
                r = parent[r]
            return r
        
        def union(x,y,parent):
            x_root = find(x, parent)
            y_root = find(y, parent)
            if x_root!=y_root:
                parent[x_root] = y_root
        
        ans = set()
        if not M:
            return 0
        for i in range(len(M)):
            for j in range(i,len(M[0])):
                if M[i][j]==1:
                    union(i,j,parent)
        print(parent)
        for i in parent:
            ans.add(find(i, parent))
        
        return len(ans)

4、优化

按秩合并：之前我们在合并时，是随机合并两个集合。
由于需要我们支持的只有集合的合并、查询操作，当我们需要将两个集合合二为一时，无论将哪一个集合连接到另一个集合的下面，都能得到正确的结果。但不同的连接方法存在时间复杂度的差异。具体来说，如果我们将一棵点数与深度都较小的集合树连接到一棵更大的集合树下，显然相比于另一种连接方案，接下来执行查找操作的用时更小（也会带来更优的最坏时间复杂度）。

解决的一个办法就是用一个数组记录每个集合的节点数。

初始化代码如下：

parent = [0]*len(M)
size = [0]*len(M)#size用来记录每棵树包含的节点数
for i in range(len(M)):
            parent[i] = i
            size[i] = 1 # 一开始只有一个节点，因此初始化节点数量为1

优化后的合并函数：

def union(x, y, parent,size):
    x_root = find(x, parent)
    y_root = find(y, parent)

    if x_root != y_root:
        # 谁的节点数多，谁就做根节点
        if size[x_root] > size[y_root]:
            parent[y_root] = x_root
            size[x_root] += size[y_root]
        else:
            parent[x_root] = y_root
            size[y_root] += size[x_root]

完整代码：

class Solution:
    def findCircleNum(self, M: List[List[int]]) -> int:
        parent = [i for i in range(len(M))]
        size = [1]*len(M)

        def find(x, parent):
            r  = x
            while r != parent[r]:
                r = parent[r]
            return r
        
        def union(x,y,parent,size):
            x_root = find(x, parent)
            y_root = find(y, parent)
            if x_root!=y_root:
                if size[x_root]<size[y_root]:
                    parent[x_root] = y_root
                    size[y_root] += size[x_root]
                else:
                    parent[y_root] = x_root
                    size[x_root] += size[y_root]

        
        ans = set()
        if not M:
            return 0
        for i in range(len(M)):
            for j in range(i,len(M[0])):
                if M[i][j]==1:
                    union(i,j,parent,size)
        print(parent)
        for i in parent:
            ans.add(find(i, parent))
        
        return len(ans)