https://zh.wikipedia.org/zh-cn/%E5%87%B8%E5%8C%85
1,增量式算法
逐次将点加入,然后检查之前的点是否在新的凸包上。由于每次都要检查所有之前的点,时间复杂度为 O ( n 2 ) {\displaystyle O(n^{2})} 。
2. 包裹法(Jarvis步进法)
首先由一点必定在凸包的点开始,例如最左的一点 A 1 {\displaystyle A_{1}} 。然后选择 A 2 {\displaystyle A_{2}} 点使得所有点都在 A 1 A 2 {\displaystyle A_{1}A_{2}} 的右方,这步骤的时间复杂度是 O ( n ) {\displaystyle O(n)} ,要比较所有点以 A 1 {\displaystyle A_{1}} 为原点的极坐标角度。以 A 2 {\displaystyle A_{2}} 为原点,重复这个步骤,依次找到 A 3 , A 4 , . . . , A k , A 1 {\displaystyle A_{3},A_{4},...,A_{k},A_{1}} 。这总共有 k {\displaystyle k} 步。因此,时间复杂度为 O ( k n ) {\displaystyle O(kn)} 。
3. 葛立恒(Graham)扫描法
由最底的一点A_1开始(如果有多个这样的点,那么选择最左边的),计算它跟其他各点的连线和x轴正向的角度,按小至大将这些点排序,称它们的对应点为 A 2 , A 3 , . . . , A n {\displaystyle A_{2},A_{3},...,A_{n}} 。这里的时间复杂度可达 O ( n log n ) {\displaystyle O(n\log {n})} 。
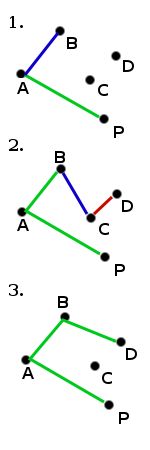
考虑最小的角度对应的点 A 3 {\displaystyle A_{3}} 。若由 A 2 {\displaystyle A_{2}} 到 A 3 {\displaystyle A_{3}} 的路径相对 A 1 {\displaystyle A_{1}} 到 A 2 {\displaystyle A_{2}} 的路径是向右转的(可以想象一个人沿 A 1 {\displaystyle A_{1}} 走到 A 2 {\displaystyle A_{2}} ,他站在 A 2 {\displaystyle A_{2}} 时,是向哪边改变方向),表示 A 3 {\displaystyle A_{3}} 不可能是凸包上的一点,考虑下一点由 A 2 {\displaystyle A_{2}} 到 A 4 {\displaystyle A_{4}} 的路径;否则就考虑 A 3 {\displaystyle A_{3}} 到 A 4 {\displaystyle A_{4}} 的路径是否向右转……直到回到 A 1 {\displaystyle A_{1}} 。
这个算法的整体时间复杂度是 O ( n log n ) {\displaystyle O(n\log {n})} ,注意每点只会被考虑一次,而不像Jarvis步进法中会考虑多次。
这个算法由葛立恒在1972年发明。[1]它的缺点是不能推广到二维以上的情况。
4. 单调链
将点按x坐标的值排列,再按y坐标的值排列。
选择x坐标为最小值的点,在这些点中找出y坐标的值最大和y坐标的值最小的点。对于x坐标为最大值也是这样处理。将两组点中y坐标值较小的点连起。在这条线段下的点,找出它们之中y坐标值最大的点,又在它们之间找x坐标值再最小和最大的点……如此类推。
时间复杂度是 O ( n log n ) {\displaystyle O(n\log {n})} 。
5. 分治法
将点集X分成两个不相交子集。求得两者的凸包后,计算这两个凸包的凸包,该凸包就是X的凸包。时间复杂度是 O ( n log n ) {\displaystyle O(n\log {n})} 。
6. 快包法(Akl-Toussaint启发式)
选择最左、最右、最上、最下的点,它们必组成一个凸四边形(或三角形)。这个四边形内的点必定不在凸包上。然后将其余的点按最接近的边分成四部分,再进行快包法(QuickHull)。