回溯算法学习体会

引言

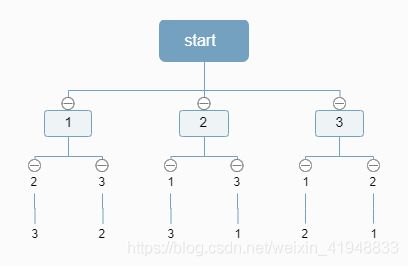
在正式谈论回溯算法以前，我们不妨以一道经典算法题作为引入。LeetCode 46. 全排列，给定一个没有重复数字的序列，返回其所有可能的全排列。 例如，输入为[1,2,3]，则输出应为[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]。我们暂时不要考虑如何用编程方式去实现这一过程，现在假设是人力罗列，我们应该遵循一个什么样的列写规则？一种简单的列写规则如下图所示。
初始时，可供我们选择的数字包含在集合｛1,2,3｝中。第一步，我们从集合中选取1作为起始节点，然后更新集合为｛2,3｝。第二步，我们从集合中选取2作为第二个节点，然后更新集合为{3}。第三步，我们从集合中选取3作为第三个节点，然后更新集合为｛｝，此时集合为空集，代表我们已经完整找到了一个可行结果[1,2,3]。回顾来看，我们每一步都在做着相同的事——从当前集合中选一个作为当前节点的数，然后更新集合。于是我们可以将问题进行抽象简化，初始时我们希望找到[1,2,3]的全排列（母问题），第一步选取1为起始节点后，我们希望找到[2,3]的全排列（子问题），因为一旦找到了[2,3]的全排列，只要在这些排列前面补上1，我们就可以得到母问题中以1为起始节点的全部结果。这就形成了用递归法求解这个问题的基本思路。
再来看图，纵观整个搜索过程，无非是一种全遍历过程。每到一个节点，如果有可选项，则生成新节点，然后更新备选集合，再进一步求解子问题；而如果无可选项，则回退到上过一个节点的状态。当然，途中我们要判断是否已经产生了解。

伪代码

反思上面的过程，我们形成一个伪代码框架，用来求解回溯问题。
整个方法其实就3大核心部件：1.解的判断以及结束判断；2.筛选满足约束的备选项；3.产生子问题并求解，求解完后恢复求解之前的状态。

public void backtrack(...){
	if(是一个可行解) 将结果存入集合中;
	if(无备选项或无须进一步搜索) return;
	
	for(所有的备选项){
		if(该备选项不满足约束) continue;
		生成当前节点;
		更新集合;
		子问题backtrack();
		//状态回退
		删除节点;
		回退集合;
	}
}

例子

全排列

LeetCode 46. 全排列
我们回顾上一节给的3大核心部件。1.解的判断以及结束判断。当temp列表的大小和给定数组的长度一致时，说明形成了一个可行结果，需要存入ret中。同时两者数值大小一致，也说明再无备选项，搜索应该回溯到上一步。2.筛选满足约束的备选项。这里用到了一个布尔数组uesd，用来记录哪些数是已经被使用了的。显然我们应该选取那些未被使用过的数。布尔数组的技巧非常实用，应该记住。3.产生子问题并求解，求解完后恢复求解之前的状态。子问题求解前需要更新布尔数组used和暂存列表temp，子问题求解完以后，需要恢复used和temp之前的状态。

class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> ret = new ArrayList<>();
        backtrack(ret,new ArrayList<Integer>(),nums,new boolean[nums.length]);
        return ret;
    }
    
    public void backtrack(List<List<Integer>> ret,List<Integer> temp,int[] nums,boolean[] used){
        if(temp.size()==nums.length){
            ret.add(new ArrayList<>(temp));
        }else{
            for(int i = 0;i<nums.length;i++){
                if(used[i]) continue;
                used[i] = true;
                temp.add(nums[i]);
                backtrack(ret,temp,nums,used);
                used[i] = false;
                temp.remove(temp.size()-1);
            }   
        }
    }
}

全排列Ⅱ

LeetCode 47. 全排列Ⅱ
相较于上一题全排列，这题最大的难点在于如何解决重复数字的排列问题。如果继续采用上一题的解法，在输入为[1,1,2]的情况下，[2,1,1]这种结果会出现2次，显然不满足题目要求。这里我们不妨回顾一下排列公式和组合公式。A(3,4) = 4*3*2，而C(3,4) = 4*3*2/(3*2*1)，两者的唯一区别在于，组合去除了排列的顺序，即组合不在乎所选3个数字的具体选择顺序是怎么样的，只在乎我们具体选择了哪3个数字。进一步，若给排列问题加上数字选择的顺序约束，即只能按照编号从小到大选择数字，其实质也将变为组合问题。回到原问题，我们能否也去除数组中这两个1的顺序性，从而避免产生重复情况。类似的，我们将固定2个1的选择顺序，只能先选择第1个1，再选择第2个1，而不存在先选择第2个1，再选择第1个1的情况。
当然在调用回溯算法以前，我们需要先对数组进行排序，从而确保相同的数是相邻的。除此之外，和上一题的唯一差别仅在于选取备选项时要求固定顺序。

class Solution {
    public List<List<Integer>> permuteUnique(int[] nums) {
        int n = nums.length;
        List<List<Integer>> ret = new ArrayList<>();
        Arrays.sort(nums);
        backtrack(ret,new ArrayList<Integer>(),nums,new boolean[n]);
        return ret;
    }
    
    //固定顺序，变组合为排列
    public void backtrack(List<List<Integer>> ret, List<Integer> temp, int[] nums, boolean[] used){
        if(temp.size()==nums.length){
            ret.add(new ArrayList<Integer>(temp));
        }else{
            int n = nums.length;
            for(int i = 0;i<n;i++){
                if(used[i] || (i>0&&nums[i]==nums[i-1]&&!used[i-1])) continue;
                used[i] = true;
                temp.add(nums[i]);
                backtrack(ret,temp,nums,used);   
                used[i] = false;
                temp.remove(temp.size()-1);    
            } 
        }
 	}  
}

组合总和

LeetCode 39. 组合总和
这题同样存在如何避免重复结果的问题。类似的，为了变排列问题为组合问题，我们对数组的全部数字固定了选择顺序——下标小的数字必须在下标大的数字之前被选择。这里不再用到布尔数组used，原因是当我们固定了选择顺序后，在每一步，我们都容易知道，下标大于当前数字的是未被选择过的，而下标小于当前数字的是已经被选择过的。

class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        int n = candidates.length;
        List<List<Integer>> ret = new ArrayList<>();
        backtrack(ret,new ArrayList<Integer>(),0,candidates,target);
        return ret;
    }
    
    public void backtrack(List<List<Integer>> ret,List<Integer> temp,int left,int[] candidates, int target){
        if(target==0){
            ret.add(new ArrayList<Integer>(temp));
        }else if(target < 0){
            return;
        }else{
            int n = candidates.length;
            for(int i =left;i<n;i++){
                temp.add(candidates[i]);
                backtrack(ret,temp,i,candidates,target-candidates[i]);
                temp.remove(temp.size()-1);
            }
        }
    }
}

总结

现在我们对回溯算法进行总结。回溯算法的本质是一种深搜递归遍历。通过上面的例题，我们可以知道回溯算法可以对各类组合、排列问题进行较好的求解，所以当遇到可以抽象建模为排列或组合的问题，回溯算法都可以作为一种求解手段。