风控模型评估指标：KS、ROC、AUC、PSI代码逻辑

上图中，我们最常用的就是TPR（True Positive Rate）和FPR（False Positive Rate）:

其中：

TPR = TP/(TP+FN)即真实1中预测错的;

FPR = FP/(FP+TN)即真实0中预测错的；

Precision = TP/(TP+FP)即预测1中对的

最理想的模型，是TPR尽量高而FPR尽量低，然而任何模型在提高正确预测概率的同时，也会难以避免地增加误判率。听起来有点抽象，好在有ROC曲线非常形象地表达了二者之间的关系。

ROC曲线是以FPR为横轴，TPR为纵轴，在不同阈值下计算FPR和TPR的值画出的图形。
AUC就是ROC曲线下方的面积，值一般在0.5-1.0之间。值越大表示模型判断准确性越高，即越接近1越好。ROC=0.5表示模型的预测能力与随机结果没有差别。
KS值表示了模型将 和-区分开来的能力。值越大，模型的预测准确性越好。一般，KS>0.2即可认为模型有比较好的预测准确性。

KS曲线与ROC有着相同的作用：

KS曲线是将概率从小到大进行排序，取10%的值为阈值，同理将10%*k(k=1,…9)处值作为阈值，计算不同的FPR和TPR，以10%*k（k=1,…9）为横坐标，同时分别以TPR和FPR为纵坐标画出两条曲线就是KS曲线。而KS值=|max(TPR-FPR)|。详细的可以参考网址：https://www.sohu.com/a/132667664_278472

另外，还有另一种计算KS值的方法：

将所有的样本根据分数值从低到高排序均分成20组，分别计算20组的实际好样本数、实际坏样本数、累积好样本数、累积坏样本数、累积好样本数占比、累积坏样本数占比、差值。其中，实际好坏样本数分别为该组内的好坏样本数；累积好坏样本数为该组累积好坏样本数；累积好坏样本数占比为累积好坏样本数占总好坏样本数的比值；差值为累积坏样本数占比 - 累积好样本数占比。
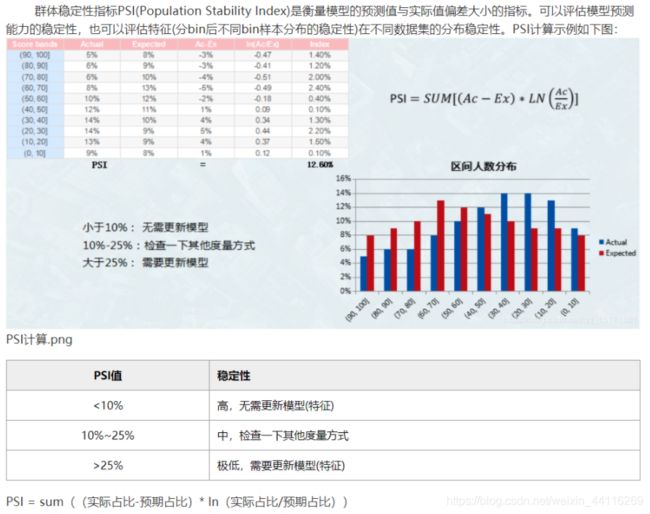
PSI在上一篇中已经做了具体介绍，想了解的可以关注我：

实现这几个指标的python代码如下：

from sklearn.metrics import roc_curve
from scipy.stats import ks_2samp

# 计算ks值
def ks_calc_auc(data,pred,y_label):
    '''
    功能: 计算KS值，输出对应分割点和累计分布函数曲线图
    输入值:
    data: 二维数组或dataframe，包括模型得分和真实的标签
    pred: 一维数组或series，代表模型得分（一般为预测正类的概率）
    y_label: 一维数组或series，代表真实的标签（{0,1}或{-1,1}）
    输出值:
    'ks': KS值
    '''
    fpr,tpr,thresholds= roc_curve(data[y_label],data[pred])
    ks = max(tpr-fpr)
    return ks

# 计算AUC值
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, roc_auc_score
def roc_auc_z(data,pred,y_label):
    # 计算auc的值
    fpr,tpr,thresholds= roc_curve(data[y_label],data[pred])
    auc_score=roc_auc_score(data[y_label],data[pred])
    return auc_score


def target_total(df,nameks,date,lable): # nameks特征名字
    # nameks特征名字
    # date分组日期：如："月份"
    # lable就是y变量
    
    
    ## 为了计算psi
    labels=['c'+str(i) for i in range(10)]
    # True_out,bins=pd.qcut(df['result'],q=10,retbins=True,labels=labels, duplicates='drop')
    True_out,bins=pd.cut(df['result'],bins=[0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1],retbins=True, labels=labels)
    df['True_out'] = True_out
    # bins[0] = bins[0]-0.001 #cut左开右闭，之前最小值再分组后组记号为空，这里减0.01划到最左侧区间
    
    ksdf = pd.DataFrame(columns=['月份'])
    month = []
    week = []
    ks = []
    roc = []
    psi = []
    for i in range(len(df[date].unique())):
        w = df[date].unique()[i]
        data_ks = df.loc[df[date] == w,]
        m = data_ks['月份'].unique()[0]
        # 计算ks值
        ks_z = ks_calc_auc(data_ks,'result',lable)
        # 计算roc_auc值
        roc_z = roc_auc_z(data_ks,'result',lable)
        
        # 计算psi值
        if len(df[date].unique())>=3:
            data_psi_last = df.loc[(df[date] <= df[date].unique()[2]),]
        else:
            fri_m = df['月份'].unique()[0]
            data_psi_last = df.loc[(df['月份'] == fri_m),]
        
        a=pd.DataFrame(data_psi_last.True_out.value_counts()).rename(columns={'True_out':'基准占比'})
        a=a.applymap(lambda y : y/sum(a.基准占比))

        b=pd.DataFrame(data_ks.True_out.value_counts()).rename(columns={'True_out':'当月占比'})
        b=b.applymap(lambda y : y/sum(b.当月占比))

        re=pd.merge(a,b,left_index=True,right_index=True)
        
        psi_z=0
        for k in range(len(re)):
            if re['基准占比'][k]==0:
                re['基准占比'][k]=0.000001
            if re['当月占比'][k]==0:
                re['当月占比'][k]=0.000001
            l=math.log((re['当月占比'][k]/re['基准占比'][k]))
            p=((re['当月占比'][k]-re['基准占比'][k])*(math.log((re['当月占比'][k]/re['基准占比'][k]))))
            
            psi_z=psi_z+p
        
        month.append(m)
        week.append(w)
        ks.append(ks_z)
        roc.append(roc_z)
        psi.append(psi_z)
        
    ksdf['月份'] = month
    ksdf[date] = week
    ksdf['features'] = nameks
    ksdf['ks'] = ks
    ksdf['roc'] = roc
    ksdf['psi'] = psi
    ksdf['psi'] = ksdf['psi']*100
    return ksdf