Gmsh网格剖分学习
Gmsh is a free 3D finite element mesh generator with a built-in CAD engine and post-processor. Its design goal is to provide a fast, light and user-friendly meshing tool with parametric input and advanced visualization capabilities.
Gmsh is built around four modules: geometry, mesh, solver and post-processing. The specification of any input to these modules is done either interactively using the graphical user interface or in ASCII text files using Gmsh’s own scripting language.
The .geo file, in fact, is a Gmsh’s scripting file. It support both C and C++ style comments.
Gmsh是一款有限元网格生成器,包含预处理、求解和后处理三大模块,分别对应于几何建模、网格优化和结果展示三项功能。
打个简单比方,张三准备建一个房子,首先将轮廓线画出来(几何建模),然后计算用多少块转(离散网格),最后再贴瓷砖或刷墙(效果展示)。
通过tutorial文件夹中的第一个简单例子t1.geo来认识其中的一些定义规则和相关的参数定义。
通过file,open打开t1.geo,出现一个方框,然后在工具栏mesh选项下找到2D,点击后方框呗离散化为三角形网格。
通过文本编辑器打开它的script t1.geo:
/*********************************************************************
*
* Gmsh tutorial 1
*
* Variables, elementary entities (points, curves, surfaces), physical
* groups (points, curves, surfaces)
*
*********************************************************************/
// The simplest construction in Gmsh's scripting language is the
// `affectation'. The following command defines a new variable `lc':
lc = 1e-2;
// This variable can then be used in the definition of Gmsh's simplest
// `elementary entity', a `Point'. A Point is defined by a list of four numbers:
// three coordinates (X, Y and Z), and a characteristic length (lc) that sets
// the target element size at the point:
Point(1) = {0, 0, 0, lc};
// The distribution of the mesh element sizes is then obtained by interpolation
// of these characteristic lengths throughout the geometry. Another method to
// specify characteristic lengths is to use general mesh size Fields (see
// `t10.geo'). A particular case is the use of a background mesh (see `t7.geo').
// We can then define some additional points as well as our first curve. Curves
// are Gmsh's second type of elementery entities, and, amongst curves, straight
// lines are the simplest. A straight line is defined by a list of point
// numbers. In the commands below, for example, the line 1 starts at point 1 and
// ends at point 2:
Point(2) = {.1, 0, 0, lc} ;
Point(3) = {.1, .3, 0, lc} ;
Point(4) = {0, .3, 0, lc} ;
Line(1) = {1,2} ;
Line(2) = {3,2} ;
Line(3) = {3,4} ;
Line(4) = {4,1} ;
// The third elementary entity is the surface. In order to define a simple
// rectangular surface from the four curves defined above, a curve loop has first
// to be defined. A curve loop is a list of connected curves, a sign being
// associated with each curve (depending on the orientation of the curve):
Curve Loop(1) = {4,1,-2,3} ;
// We can then define the surface as a list of curve loops (only one here, since
// there are no holes--see `t4.geo'):
Plane Surface(1) = {1} ;
// At this level, Gmsh knows everything to display the rectangular surface 6 and
// to mesh it. An optional step is needed if we want to group elementary
// geometrical entities into more meaningful groups, e.g. to define some
// mathematical ("domain", "boundary"), functional ("left wing", "fuselage") or
// material ("steel", "carbon") properties.
//
// Such groups are called "Physical Groups" in Gmsh. By default, if physical
// groups are defined, Gmsh will export in output files only those elements that
// belong to at least one physical group. (To force Gmsh to save all elements,
// whether they belong to physical groups or not, set "Mesh.SaveAll=1;", or
// specify "-save_all" on the command line.)
//
// Here we define a physical curve that groups the left, bottom and right lines
// in a single group (with prescribed tag 5); and a physical surface with name
// "My surface" (with an automatic tag) containg the geometrical surface 1:
Physical Curve(5) = {1, 2, 4} ;
Physical Surface("My surface") = {1} ;
// Note that starting with Gmsh 3.0, models can be built using different
// geometry kernels than the default "built-in" kernel. By specifying
//
// SetFactory("OpenCASCADE");
//
// any subsequent command in the .geo file would be handled by the OpenCASCADE
// geometry kernel instead of the built-in kernel. A rectangular surface could
// then simply be created with
//
// Rectangle(2) = {.2, 0, 0, 0.1, 0.3};
//
// See tutorial/t16.geo for a complete example, and demos/boolean for more.
其中,我们需要知道的四个语句:
1: 定义参数 lc = 1e-2;
2: 定义点 Point(1) = {0,0,0,lc};
3: 定义线段 Line(1) = {1,2};
4: 定义闭合线段 Line Loop(5) = {4,1,-2,3};
5: 定义面 Plane Surface(6) = {5}
由此,Gmsh参数化建模的流程:**通过参数定义点的属性,连接相应的点构成线段,在连接一系列线段构成封闭的面。**其中,定义点需要四个变量,分别为:三个坐标和一个定义网格剖分疏密的参数。
几个最为实用的选项设置:
1)菜单tool中Options选项Visibility:
该选项卡里Geometry和Mesh里Visibility包含了点、线、面的显示参数;
2)菜单tool中Options—General—Advanced:
当设置参数没有变化,也找不出原因时,回复默认设置是有效的选择;
3)菜单tool中Options—General 脚本重载于编辑:
Gmsh支持前台和后台双重操作,也就是说,用户可以在后台编辑脚本,但后通过导航栏Geometry下面的Reload重新加载,相应实图会自动更新;
除此以外,用户也可以在前台通过鼠标建模(选点、连线、取面等),对应的命令语句会自动卸乳对应的脚本文件(在导航栏的Geometry—Edit file可以自动打开脚本文件,可以非常直观的学习脚本命令)。当然用户也可以进行混合操作。
一个简单里操作栗子,及其中的网格形态设置(三角形、四边形、规则四边形及网格尺寸),可以参考http://www.docin.com/p-1856905616.html进行详细了解。
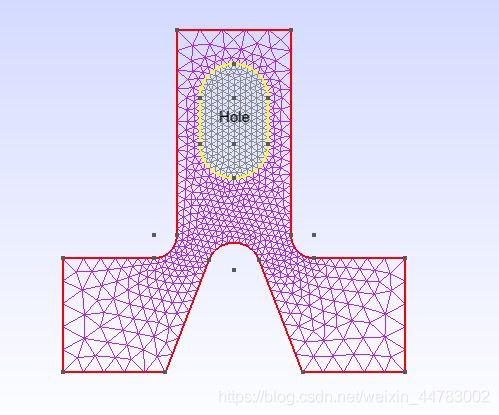
带圆弧的形状
此处再看一下tutorial文件夹中的第四个带圆弧的例子t4.geo:
/*********************************************************************
*
* Gmsh tutorial 4
*
* Built-in functions, surface holes, annotations, mesh colors
*
*********************************************************************/
// As usual, we start by defining some variables:
cm = 1e-02;
e1 = 4.5 * cm; e2 = 6 * cm / 2; e3 = 5 * cm / 2;
h1 = 5 * cm; h2 = 10 * cm; h3 = 5 * cm; h4 = 2 * cm; h5 = 4.5 * cm;
R1 = 1 * cm; R2 = 1.5 * cm; r = 1 * cm;
Lc1 = 0.01;
Lc2 = 0.003;
// We can use all the usual mathematical functions (note the capitalized first
// letters), plus some useful functions like Hypot(a, b) := Sqrt(a^2 + b^2):
ccos = (-h5*R1 + e2 * Hypot(h5, Hypot(e2, R1))) / (h5^2 + e2^2);
ssin = Sqrt(1 - ccos^2);
// Then we define some points and some lines using these variables:
Point(1) = {-e1-e2, 0 , 0, Lc1}; Point(2) = {-e1-e2, h1 , 0, Lc1};
Point(3) = {-e3-r , h1 , 0, Lc2}; Point(4) = {-e3-r , h1+r , 0, Lc2};
Point(5) = {-e3 , h1+r , 0, Lc2}; Point(6) = {-e3 , h1+h2, 0, Lc1};
Point(7) = { e3 , h1+h2, 0, Lc1}; Point(8) = { e3 , h1+r , 0, Lc2};
Point(9) = { e3+r , h1+r , 0, Lc2}; Point(10)= { e3+r , h1 , 0, Lc2};
Point(11)= { e1+e2, h1 , 0, Lc1}; Point(12)= { e1+e2, 0 , 0, Lc1};
Point(13)= { e2 , 0 , 0, Lc1};
Point(14)= { R1 / ssin, h5+R1*ccos, 0, Lc2};
Point(15)= { 0 , h5 , 0, Lc2};
Point(16)= {-R1 / ssin, h5+R1*ccos, 0, Lc2};
Point(17)= {-e2 , 0.0 , 0, Lc1};
Point(18)= {-R2 , h1+h3 , 0, Lc2}; Point(19)= {-R2 , h1+h3+h4, 0, Lc2};
Point(20)= { 0 , h1+h3+h4, 0, Lc2}; Point(21)= { R2 , h1+h3+h4, 0, Lc2};
Point(22)= { R2 , h1+h3 , 0, Lc2}; Point(23)= { 0 , h1+h3 , 0, Lc2};
Point(24)= { 0, h1+h3+h4+R2, 0, Lc2}; Point(25)= { 0, h1+h3-R2, 0, Lc2};
Line(1) = {1 , 17};
Line(2) = {17, 16};
// Gmsh provides other curve primitives than straight lines: splines, B-splines,
// circle arcs, ellipse arcs, etc. Here we define a new circle arc, starting at
// point 14 and ending at point 16, with the circle's center being the point 15:
Circle(3) = {14,15,16};
// Note that, in Gmsh, circle arcs should always be smaller than Pi. We can then
// define additional lines and circles, as well as a new surface:
Line(4) = {14,13}; Line(5) = {13,12}; Line(6) = {12,11};
Line(7) = {11,10}; Circle(8) = {8,9,10}; Line(9) = {8,7};
Line(10) = {7,6}; Line(11) = {6,5}; Circle(12) = {3,4,5};
Line(13) = {3,2}; Line(14) = {2,1}; Line(15) = {18,19};
Circle(16) = {21,20,24}; Circle(17) = {24,20,19};
Circle(18) = {18,23,25}; Circle(19) = {25,23,22};
Line(20) = {21,22};
Curve Loop(21) = {17,-15,18,19,-20,16};
Plane Surface(22) = {21};
// But we still need to define the exterior surface. Since this surface has a
// hole, its definition now requires two curves loops:
Curve Loop(23) = {11,-12,13,14,1,2,-3,4,5,6,7,-8,9,10};
Plane Surface(24) = {23,21};
// As a general rule, if a surface has N holes, it is defined by N+1 curve loops:
// the first loop defines the exterior boundary; the other loops define the
// boundaries of the holes.
// Finally, we can add some comments by embedding a post-processing view
// containing some strings:
View "comments" {
// Add a text string in window coordinates, 10 pixels from the left and 10
// pixels from the bottom, using the StrCat function to concatenate strings:
T2(10, -10, 0){ StrCat("Created on ", Today, " with Gmsh") };
// Add a text string in model coordinates centered at (X,Y,Z) = (0, 0.11, 0):
T3(0, 0.11, 0, TextAttributes("Align", "Center", "Font", "Helvetica")){ "Hole" };
// If a string starts with `file://', the rest is interpreted as an image
// file. For 3D annotations, the size in model coordinates can be specified
// after a `@' symbol in the form `widthxheight' (if one of `width' or
// `height' is zero, natural scaling is used; if both are zero, original image
// dimensions in pixels are used):
T3(0, 0.09, 0, TextAttributes("Align", "Center")){ "file://[email protected]" };
// The 3D orientation of the image can be specified by proving the direction
// of the bottom and left edge of the image in model space:
T3(-0.01, 0.09, 0, 0){ "file://[email protected],0,0,1,0,1,0" };
// The image can also be drawn in "billboard" mode, i.e. always parallel to
// the camera, by using the `#' symbol:
T3(0, 0.12, 0, TextAttributes("Align", "Center")){ "file://[email protected]#" };
// The size of 2D annotations is given directly in pixels:
T2(350, -7, 0){ "file://t4_image.png@20x0" };
};
// Views and geometrical entities can be made to respond to double-click events:
View[0].DoubleClickedCommand = "Printf('View[0] has been double-clicked!');";
Geometry.DoubleClickedLineCommand = "Printf('Curve %g has been double-clicked!',
Geometry.DoubleClickedEntityTag);";
// We can also change the color of some mesh entities:
Color Grey50{ Surface{ 22 }; }
Color Purple{ Surface{ 24 }; }
Color Red{ Curve{ 1:14 }; }
Color Yellow{ Curve{ 15:20 }; }
生成带边界条件的网格
参考
gmsh中的元素可以分成两类:几何实体和物理实体。几何实体是网格元素的最基本组成,物理实体(物理组)则是在几何元素的基础上进行逻辑层上的分类。从架构上看,几何实体属于物理划分,物理实体则是逻辑划分。
gmsh支持根据物理性质将几何实体进行归类和划分。目前所知物理实体一个非常重要的性质是设定网格的边界条件:将相同边界条件的几何元素归到同一个组下,gmsh在生成网格的时候就将物理信息写入到生成的网格信息中。
物理实体的定义需要在定义的元素前加上”Physical”标识符,其余的同几何实体的定义相同。下面是一个二维机翼的gmsh定义:
cl_1 = 0.01;
Point(1) = {1, 0, 0, cl_1};
Point(2) = {0.2906701309999999, 0, 0.059599889, cl_1};
Point(3) = {0.290670131, 0, 0.059599889, cl_1};
Point(4) = {-3.33066907387547e-016, 0, -2.775557561562891e-017, cl_1};
Point(5) = {0.290670131, 0, -0.059599889, cl_1};
Point(6) = {-1.110223024625156e-016, 0, 0, cl_1};
Point(7) = {1, 0, 0, cl_1};
Point(8) = {0.2906701309999999, 0, -0.059599889, cl_1};
p1 = newp;
Point(p1 + 1) = {0.9578477628235885, 0, 0.005808055788066277};
Point(p1 + 2) = {0.9136001717514742, 0, 0.01159953317971515};
Point(p1 + 3) = {0.8678598741632115, 0, 0.01728526031819392};
Point(p1 + 4) = {0.8212779475631614, 0, 0.02277865740518693};
Point(p1 + 5) = {0.7745191250941298, 0, 0.02800031778249978};
Point(p1 + 6) = {0.7282262993505407, 0, 0.03288198060276357};
Point(p1 + 7) = {0.6829880771923493, 0, 0.0373694940386463};
Point(p1 + 8) = {0.6393125213400493, 0, 0.04142453011683183};
Point(p1 + 9) = {0.5976090881089672, 0, 0.04502500226786509};
Point(p1 + 10) = {0.5581794445899648, 0, 0.0481643117667218};
Point(p1 + 11) = {0.521216620190355, 0, 0.05084967643767647};
Point(p1 + 12) = {0.4868110356265319, 0, 0.05309985880292391};
Point(p1 + 13) = {0.4549614552219337, 0, 0.05494261362247144};
Point(p1 + 14) = {0.4255888082703554, 0, 0.05641213152223604};
Point(p1 + 15) = {0.3985510271977428, 0, 0.05754668640628761};
Point(p1 + 16) = {0.3736574289168878, 0, 0.05838661862754537};
Point(p1 + 17) = {0.3506816041400513, 0, 0.0589727173733007};
Point(p1 + 18) = {0.3293721908004415, 0, 0.05934501212155738};
Point(p1 + 19) = {0.309461241465114, 0, 0.0595419466863262};
Spline(1) = {1, p1 + 1, p1 + 2, p1 + 3, p1 + 4, p1 + 5, p1 + 6, p1 + 7, p1 + 8, p1 + 9, p1 + 10, p1 + 11, p1 + 12, p1 + 13, p1 + 14, p1 + 15, p1 + 16, p1 + 17, p1 + 18, p1 + 19, 2};
p2 = newp;
Point(p2 + 1) = {0.2842729112131264, 0, 0.05959035601288155};
Point(p2 + 2) = {0.2761001220809002, 0, 0.0595451957195354};
Point(p2 + 3) = {0.2666300877434753, 0, 0.05944430161792291};
Point(p2 + 4) = {0.2560533097681484, 0, 0.05926870849763945};
Point(p2 + 5) = {0.2444412386433862, 0, 0.05899746041353254};
Point(p2 + 6) = {0.2318090344278302, 0, 0.058605806668528};
Point(p2 + 7) = {0.2181439021461914, 0, 0.05806365702589601};
Point(p2 + 8) = {0.2034209651627122, 0, 0.05733392771630338};
Point(p2 + 9) = {0.1876150065513268, 0, 0.0563705983368452};
Point(p2 + 10) = {0.1707120994729877, 0, 0.0551163616335265};
Point(p2 + 11) = {0.1527237978253341, 0, 0.05349978292686403};
Point(p2 + 12) = {0.1337063457254963, 0, 0.05143193572045287};
Point(p2 + 13) = {0.1137876774535901, 0, 0.04880258242681034};
Point(p2 + 14) = {0.09320552798189294, 0, 0.04547617760131762};
Point(p2 + 15) = {0.07236044644973513, 0, 0.04128836888014319};
Point(p2 + 16) = {0.05188730831459138, 0, 0.03604437967545813};
Point(p2 + 17) = {0.03274685573930983, 0, 0.02952182506630169};
Point(p2 + 18) = {0.01633265015110124, 0, 0.0214822334050408};
Point(p2 + 19) = {0.004575175047531102, 0, 0.01169763023104438};
Spline(2) = {3, p2 + 1, p2 + 2, p2 + 3, p2 + 4, p2 + 5, p2 + 6, p2 + 7, p2 + 8, p2 + 9, p2 + 10, p2 + 11, p2 + 12, p2 + 13, p2 + 14, p2 + 15, p2 + 16, p2 + 17, p2 + 18, p2 + 19, 4};
p3 = newp;
Point(p3 + 1) = {0.2842687444062102, 0, -0.05959033995136771};
Point(p3 + 2) = {0.2760902965551228, 0, -0.05954510785780694};
Point(p3 + 3) = {0.2666128650422044, 0, -0.05944404536989124};
Point(p3 + 4) = {0.2560272811856329, 0, -0.05926814784851871};
Point(p3 + 5) = {0.2444053852046738, 0, -0.05899642178635941};
Point(p3 + 6) = {0.2317627182952431, 0, -0.05860407976787362};
Point(p3 + 7) = {0.2180868707188054, 0, -0.05806099563459484};
Point(p3 + 8) = {0.203353381935633, 0, -0.05733005183556716};
Point(p3 + 9) = {0.1875375094086677, 0, -0.05636519948112355};
Point(p3 + 10) = {0.1706258837914739, 0, -0.05510911382545057};
Point(p3 + 11) = {0.1526307187728704, 0, -0.05349036308954442};
Point(p3 + 12) = {0.1336090279833125, 0, -0.05142005881221923};
Point(p3 + 13) = {0.1136896084213433, 0, -0.0487880588136444};
Point(p3 + 14) = {0.09311108862650791, 0, -0.04545900258153844};
Point(p3 + 15) = {0.07227479757675123, 0, -0.04126885612468364};
Point(p3 + 16) = {0.05181599481494702, 0, -0.03602334947685121};
Point(p3 + 17) = {0.03269491843986368, 0, -0.02950085009913444};
Point(p3 + 18) = {0.01630296371554681, 0, -0.02146392080930703};
Point(p3 + 19) = {0.004565723668620725, 0, -0.01168586711270097};
Spline(3) = {5, p3 + 1, p3 + 2, p3 + 3, p3 + 4, p3 + 5, p3 + 6, p3 + 7, p3 + 8, p3 + 9, p3 + 10, p3 + 11, p3 + 12, p3 + 13, p3 + 14, p3 + 15, p3 + 16, p3 + 17, p3 + 18, p3 + 19, 6};
Reverse Line {3};
p4 = newp;
Point(p4 + 1) = {0.9578371307341608, 0, -0.005809451776204171};
Point(p4 + 2) = {0.9135836204677359, 0, -0.01160162204700566};
Point(p4 + 3) = {0.8678423367489414, 0, -0.01728739358632329};
Point(p4 + 4) = {0.8212641228333738, 0, -0.02278029282335023};
Point(p4 + 5) = {0.7745130557952343, 0, -0.02800105787177528};
Point(p4 + 6) = {0.7282310363923532, 0, -0.03288159346440879};
Point(p4 + 7) = {0.6830054673847058, 0, -0.03736791477271506};
Point(p4 + 8) = {0.6393431339409602, 0, -0.04142184433789697};
Point(p4 + 9) = {0.5976522728176452, 0, -0.04502141572787306};
Point(p4 + 10) = {0.5582334954732195, 0, -0.04816011152865139};
Point(p4 + 11) = {0.5212790094647602, 0, -0.05084518927366299};
Point(p4 + 12) = {0.4868786787883632, 0, -0.05309541172223745};
Point(p4 + 13) = {0.4550309732288671, 0, -0.05493850005863926};
Point(p4 + 14) = {0.4256567607517621, 0, -0.05640858514472293};
Point(p4 + 15) = {0.398614100322739, 0, -0.05754386310405684};
Point(p4 + 16) = {0.373712570479338, 0, -0.05838458613465396};
Point(p4 + 17) = {0.3507261053773512, 0, -0.05897145133181579};
Point(p4 + 18) = {0.3294037189943399, 0, -0.05934439706944743};
Point(p4 + 19) = {0.3094778295903463, 0, -0.05954178043174179};
Spline(4) = {7, p4 + 1, p4 + 2, p4 + 3, p4 + 4, p4 + 5, p4 + 6, p4 + 7, p4 + 8, p4 + 9, p4 + 10, p4 + 11, p4 + 12, p4 + 13, p4 + 14, p4 + 15, p4 + 16, p4 + 17, p4 + 18, p4 + 19, 8};
Coherence;
cl_2 = 2.0;
Point(89) = {-20, 0, 20, cl_2};
Point(90) = {-20, 0, -20, cl_2};
Point(91) = {20, 0, -20, cl_2};
Point(92) = {20, 0, 20, cl_2};
Line(7) = {89, 92};
Line(8) = {92, 91};
Line(9) = {91, 90};
Line(10) = {90, 89};
Line Loop(11) = {10, 7, 8, 9};
Line Loop(12) = {1, 2, -3, -4};
Plane Surface(13) = {11, 12};
Physical Line(14) = {9, 7, 10, 8};
Physical Line(15) = {1, 2, 3, 4};
Physical Surface(1) = {13};
上述文件定义了一个二维机翼的几何实体和物理实体。将其使用gmsh则可生成二维的网格。
注意: 如果需要导出msh格式,必须给出完整的physical定义!在上述例子中,如果没有给出最后的physical surface定义,保存成msh的格式则只有边界上的数据。话句话说,如果定义了物理实体,msh格式只会输出和physical信息的几何实体相关的网格!