2.Regression-Case Study

回归问题：

        The output of the target function f is “scalar”.

课程用例说明：

        针对的问题：估计pokemon进化之后的CP值（战斗力），来讲解什么是Regression

        如上面图中所示，我们的目标是在函数‘f’中，input一只宝可梦，output他进化后的cp值。 那么寻找这个函数 f 就成了问题的关键。

Step1：选择模型

        注意：现只考虑一个参数即当前CP值

                   建立模型，比如我们就在这里建立一个Linear model：

        可见，不同的b、w，得到的 f 不尽相同，而下面，我们就要找到最能契合要求的一个 f。

Step2：模型好坏

        可以看到，当我们将准备好的training data（已知10个宝可梦的进化情况），建立一个二维坐标轴。

         通过上图可以看出，似乎有一个函数能够拟合这些坐标点，而这就是我们想要的，为了选出最契合的 f ，我们要建立一个Loss function L ，也就是函数的损失函数。

Loss function L
input	a function
output	how bad it is

       如果我们将 f 的 w 和 b 作为两轴，则在下图中每一点都代表一个 function f ，而颜色代表output的大小，也就代表该function f 参数的好坏。易理解，smallest点做对应的函数 f 就是我们想要的。

Step3：最佳函数/模型

       我们刚刚提到最拟合的 f ，他可能是 y = 0.6x +0.8，这个就叫做best function，那么我们该用什么方法在Loss Function下找到它呢？这个L(w，b）smallest该如何计算呢？

       首先容易想到的，在本案例中，我们可以用线性代数的基本公式来直接计算出最佳w和b。

        除了这种方法，当特征值非常多时，我们就要用到梯度下降法来进行计算。

       当我们在L（w）的二维平面中时，我们必须要找到函数的最低点。

       首先随机选取一个点w0，计算微分也就是斜率，如果为正，则减小w(w左移)，如果为负，则增大w(w右移)。而这有另一个问题，每次要增加或减少多少w值呢，有两个因素影响。第一，即微分值，如果微分值很大或很小，表示此处非常陡峭，那么证明距离最低点还有很远的距离，所以移动的距离就很大。第二个因素是我们事先自主定义的常数项 η 值(学习率)，即步长。

       按照这个模式，不断重复，经过非常多的参数更新后，能达到一个最低点。

       当我们有多个feature时，即不仅有 w 还有 b ，同样不会影响梯度下降过程，展示出来就是这样的：

      说到这里大家可能会担心，会不会产生下图左半部分的哪种情况，即不同的起始位置，找到的最低点是不一样的，那么这里的解释是，在我们案例的Linear regression中，不会出现这种可能性，而全都是右图哪种形式，原因是其为线性的。

         通过这种方式，我们就能得到想要的 function f ，来解决我们的需求。

How’s the results?

       通过上面的计算，我们成功得到了一个如图函数 f，接下来就会发现，并不是所有的点都能拟合函数，这就会造成很大的预测不准的情况，通过Loss Function也能看出，最优解的值依然很大，测试数据的表现也不好，所以我们就要想办法优化。Average Error on Testing Data＞Average Error on Training Data,这个很容易理解，因为model就是根据Training Data拟合出来的。

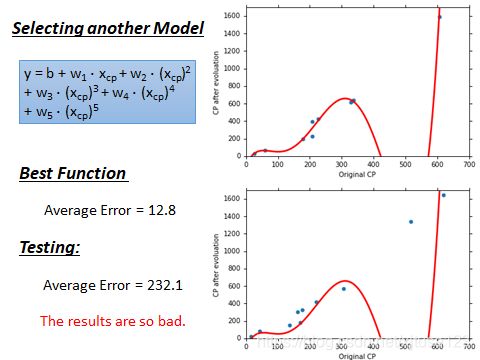
      很容易想到，刚刚我们用了一次方程作为model，二次方程会不会更好一些呢，三次方程、四次方程呢？于是我们做了以下实验，用同样的方法，放到多次方程中。

 overfitting

      通过上面四幅图可以看出，虽然当我们增加函数次数时，可以使training data的Average Error越来越小(上一次都是下一次的子集)，但是Test data的表现却不尽如人意，甚至在五次方程时，大大超出了我们的预估，那么这种现象就叫做overfitting。

       所以，function不是越复杂越好，所以我们要选择一个最合适的，由上图可以看出，在三次方程中表现最好。有一个万能的提高准确率的好方法，收集更多的数据。 Les’s collect more data。

其他隐藏的因素：

        首先，当然是将物种因素考虑进来，对于物种因素，当其为不同的物种，其函数也不同。写成一个线性模型，利用δ 函数，将模型写成了一个线性函数的形式。如当物种为Pidgey时，无关项都变为了0：

       其次，重量、高度、HP值这些隐藏因素也考虑进入。

       经过上一步，效果还是很不理想，这个时候修改损失函数，损失函数在多加一项。Back to step 2: 正则化，要多平滑？通过λ 来得到最佳模型。对于训练误差：λ越大，考虑训练误差越少。我们要平滑的函数，但不能太平滑