tensorflow笔记第六讲RNN

• 我们通过上一讲的CNN，可以知道，CNN是依据于尺寸不变性，平移不变性，旋转不变性。空间共享，通过不同位置的参数共享
• 那么接下来，我们来学习时间共享，通过不同时刻的参数共享。
  

循环核

• 循环核：参数时间共享，循环层提取时间信息。
• 记忆体内存储的状态信息ht，在每个时刻都被更新
  

循环横向 按时间展开

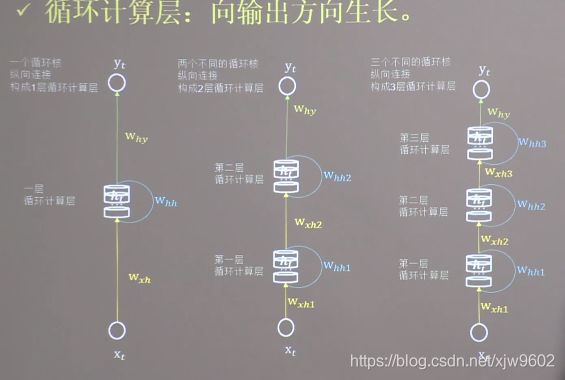
循环计算层

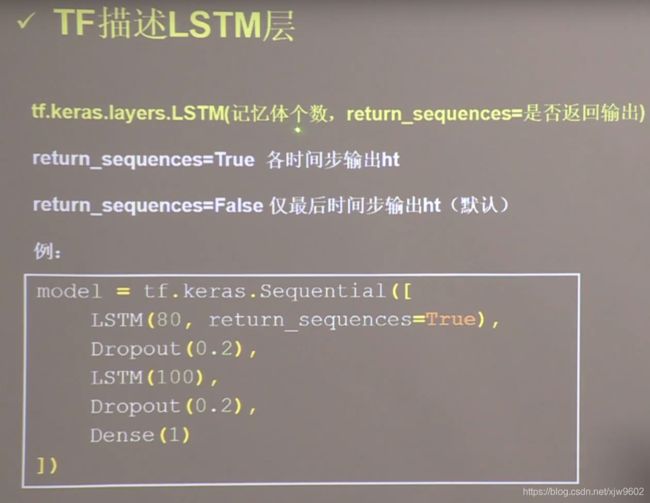
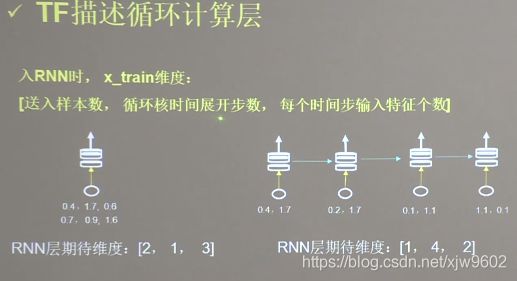
TF描述循环计算层

• return_sequences = True
  
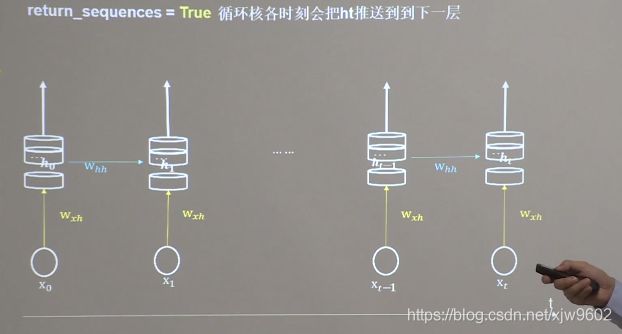
• return_sequences = False
  
• x_train维度【送入样本数，循环核时间展开步数，每个时间步输入特征个数】
• 循环核展开步数，也就是输入的一个数据，有几个字符，就是几。比如输入是a，那么展开步数是1，输入是AAT，那么展开步数是3
• 另外，每个时间步输入特征个数 也就是每个字符用几个特征数值表示，比如 A（ATCG） 在one-hot编码中，用n来表示，也就是每个时间步输入特征个数为n。n表示序列长度。
  

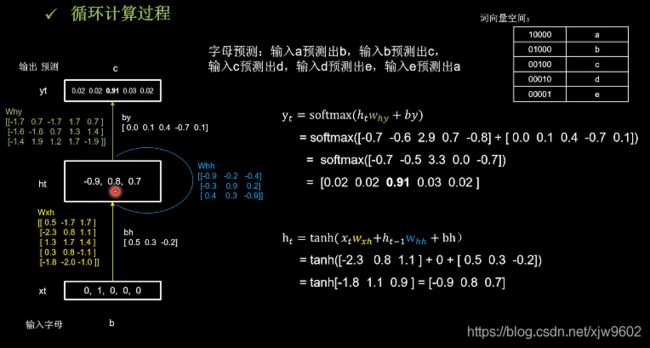
循环计算过程

Embedding编码

• embedding编码作为可训练的参数，设定词汇表大小，每个字符的维度即可
  

RNN实现股票预测

import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dropout, Dense, SimpleRNN
import matplotlib.pyplot as plt
import os
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error
import math

maotai = pd.read_csv('./SH600519.csv')  # 读取股票文件

training_set = maotai.iloc[0:2426 - 300, 2:3].values  # 前(2426-300=2126)天的开盘价作为训练集,表格从0开始计数，2:3 是提取[2:3)列，前闭后开,故提取出C列开盘价
test_set = maotai.iloc[2426 - 300:, 2:3].values  # 后300天的开盘价作为测试集

# 归一化
sc = MinMaxScaler(feature_range=(0, 1))  # 定义归一化：归一化到(0，1)之间
training_set_scaled = sc.fit_transform(training_set)  # 求得训练集的最大值，最小值这些训练集固有的属性，并在训练集上进行归一化
test_set = sc.transform(test_set)  # 利用训练集的属性对测试集进行归一化

x_train = []
y_train = []

x_test = []
y_test = []

# 测试集：csv表格中前2426-300=2126天数据
# 利用for循环，遍历整个训练集，提取训练集中连续60天的开盘价作为输入特征x_train，第61天的数据作为标签，for循环共构建2426-300-60=2066组数据。
for i in range(60, len(training_set_scaled)):
    x_train.append(training_set_scaled[i - 60:i, 0])
    y_train.append(training_set_scaled[i, 0])
# 对训练集进行打乱
np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
tf.random.set_seed(7)
# 将训练集由list格式变为array格式
x_train, y_train = np.array(x_train), np.array(y_train)

# 使x_train符合RNN输入要求：[送入样本数， 循环核时间展开步数， 每个时间步输入特征个数]。
# 此处整个数据集送入，送入样本数为x_train.shape[0]即2066组数据；输入60个开盘价，预测出第61天的开盘价，循环核时间展开步数为60; 每个时间步送入的特征是某一天的开盘价，只有1个数据，故每个时间步输入特征个数为1
x_train = np.reshape(x_train, (x_train.shape[0], 60, 1))
# 测试集：csv表格中后300天数据
# 利用for循环，遍历整个测试集，提取测试集中连续60天的开盘价作为输入特征x_train，第61天的数据作为标签，for循环共构建300-60=240组数据。
for i in range(60, len(test_set)):
    x_test.append(test_set[i - 60:i, 0])
    y_test.append(test_set[i, 0])
# 测试集变array并reshape为符合RNN输入要求：[送入样本数， 循环核时间展开步数， 每个时间步输入特征个数]
x_test, y_test = np.array(x_test), np.array(y_test)
x_test = np.reshape(x_test, (x_test.shape[0], 60, 1))

model = tf.keras.Sequential([
    SimpleRNN(80, return_sequences=True),
    Dropout(0.2),
    SimpleRNN(100),
    Dropout(0.2),
    Dense(1)
])

model.compile(optimizer=tf.keras.optimizers.Adam(0.001),
              loss='mean_squared_error')  # 损失函数用均方误差
# 该应用只观测loss数值，不观测准确率，所以删去metrics选项，一会在每个epoch迭代显示时只显示loss值

checkpoint_save_path = "./checkpoint/rnn_stock.ckpt"

if os.path.exists(checkpoint_save_path + '.index'):
    print('-------------load the model-----------------')
    model.load_weights(checkpoint_save_path)

cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_save_path,
                                                 save_weights_only=True,
                                                 save_best_only=True,
                                                 monitor='val_loss')

history = model.fit(x_train, y_train, batch_size=64, epochs=50, validation_data=(x_test, y_test), validation_freq=1,
                    callbacks=[cp_callback])

model.summary()

file = open('./weights.txt', 'w')  # 参数提取
for v in model.trainable_variables:
    file.write(str(v.name) + '\n')
    file.write(str(v.shape) + '\n')
    file.write(str(v.numpy()) + '\n')
file.close()

loss = history.history['loss']
val_loss = history.history['val_loss']

plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
plt.title('Training and Validation Loss')
plt.legend()
plt.show()

################## predict ######################
# 测试集输入模型进行预测
predicted_stock_price = model.predict(x_test)
# 对预测数据还原---从（0，1）反归一化到原始范围
predicted_stock_price = sc.inverse_transform(predicted_stock_price)
# 对真实数据还原---从（0，1）反归一化到原始范围
real_stock_price = sc.inverse_transform(test_set[60:])
# 画出真实数据和预测数据的对比曲线
plt.plot(real_stock_price, color='red', label='MaoTai Stock Price')
plt.plot(predicted_stock_price, color='blue', label='Predicted MaoTai Stock Price')
plt.title('MaoTai Stock Price Prediction')
plt.xlabel('Time')
plt.ylabel('MaoTai Stock Price')
plt.legend()
plt.show()

##########evaluate##############
# calculate MSE 均方误差 ---> E[(预测值-真实值)^2] (预测值减真实值求平方后求均值)
mse = mean_squared_error(predicted_stock_price, real_stock_price)
# calculate RMSE 均方根误差--->sqrt[MSE]    (对均方误差开方)
rmse = math.sqrt(mean_squared_error(predicted_stock_price, real_stock_price))
# calculate MAE 平均绝对误差----->E[|预测值-真实值|](预测值减真实值求绝对值后求均值）
mae = mean_absolute_error(predicted_stock_price, real_stock_price)
print('均方误差: %.6f' % mse)
print('均方根误差: %.6f' % rmse)
print('平均绝对误差: %.6f' % mae)

LSTM

LSTM就是听老师讲课的过程，现在脑子记忆的内容是ppt第一页到第45页记忆的长期记忆内容Ct，长期记忆Ct包括两部分，一部分是ppt1-44页的内容，也就是上一时刻的Ct-1，因为不可能全部记住，所以需要乘上遗忘门，这个乘积项表示留存在脑中的对过去的记忆。现在学习的是新知识，是即将存入脑中的现在的记忆。现在的记忆包括两部分，一部分是现在讲的第45页ppt，是当前时刻输入的Xt，还有一部分是第44页ppt的短期记忆留存，脑袋把当前时刻的输入Xt和上一时刻的短期记忆ht-1，归纳形成即将存入脑中的现在的记忆Ct波浪号。现在的记忆乘以输入门与过去的记忆异同存储Wie长期记忆。当我重新讲给别人时，不可能一字不落的讲出来，讲的是留存在脑中的长期记忆经过输出门筛选后的内容，这就是记忆体的输出ht。

当有多层网络时，第二层循环网络的输入就是第一层循环网络的输出ht，输入第二层网络的是第一层网络提取的精华。

• TF表示
  

GRU网络

• TF描述