算法笔记 - 树图
第十二章 - 二叉树
12.1 普通二叉树的建立(由中序遍历和后序遍历创建二叉树)
//定义节点
struct node
{
int data;
node * lchild;
node * rchild;
}
//输入 int in[MAX];int post[MAX]; 中序遍历和后序遍历
//创建二叉树 node * root =create(0,n-1,0,n-1);
node* create(int inL,int inR,int postL,int postR)
{
//递归边界
if(postL>postR) return NULL;
//建立根节点实体
node * root =new node;
node->data=post[postR];
//在中序遍历中找到根节点下标
int k=0;
for(int i=inL;i<=inR;i++)//注意查找范
{
if(in[i]==post[postR])
{k=i;break;}
}
//递归创建左右子树
root->lchild=create(inL,k-1,postL,postL+(k-inL)-1);
root->rchild=create(k+1,inR,postL+(k-inL),postR-1);
//出口
return root;
}
//定义 层次序列 int level[MAX];
//层次遍历 BFS(root);
void BFS(node* root)
{
queue12.2 BST二叉搜索树创建
//定义节点
struct node
{
int data;
node *lchild;
node *rchild;
}
//定义 node *root = NULL;
//输入 插入序列vector bst; 边输入边插入
void insert(node* &root,int data)//注意使用引用
{
//找到底层就插入
if(root==NULL)
{
root = new node;//注意之前root只是一个空指针没有指向真正的实体
root->data = data ;
root->lchild=NULL;
root->rchild=NULL;
return ;
}
//否则递归找底层
if(root->data<=data) insert(root->rchild,data);
else insert(root->lchild,data);
return ;
}12.3 二叉搜索树遍历
//先序遍历,结果存在vi中
void pre(node *root,vector<int> &vi)//注意是引用
{
if(root == NULL) return ;
vi.push_back(root->data);
pre(root->lchild,vi);
pre(root->rchild,vi);
}
//中序遍历
void in(node *root ,vector<int> &vi)
{
if(root == NULL) return ;
pre(root->lchild,vi);
vi.push_back(root->data);
pre(root->rchild,vi);
}
//后序遍历
void post(node *root ,vector<int> &vi)
{
if(root == NULL) return ;
pre(root->lchild,vi);
pre(root->rchild,vi);
vi.push_back(root->data);
}
//层序遍历
void BFS(node *root,vector<int> &vi)
{
queue12.4 并查集(每个集合都是一棵树)
//定义 朋友圈int father[MAX];朋友圈大佬 int isroot[MAX];
//输入 人数n和朋友圈数m
//初始化朋友圈
for(int i=0;i0;
//输入朋友对(a,b),合并
void union(int a, int b)
{
int faA=findfather(a);
int faB=findfather(b);
if(faA!=FaB)
father[faB]=faA;
}
int findfather(int a)
{
//找
int temp =a;
while(a!=father[a]) a=father[a];
//压缩
while(temp!=father[temp])
{
int k =temp;
temp=father[temp];
father[k]=a;
}
return a;
}
//遍历每一个人记录 圈数和圈内人数
for(int i=0;ifor(int i=0;iif(isroot[i]>0) ans++; 4109 公共朋友 (朋友关系不可传递,不是并查集!)

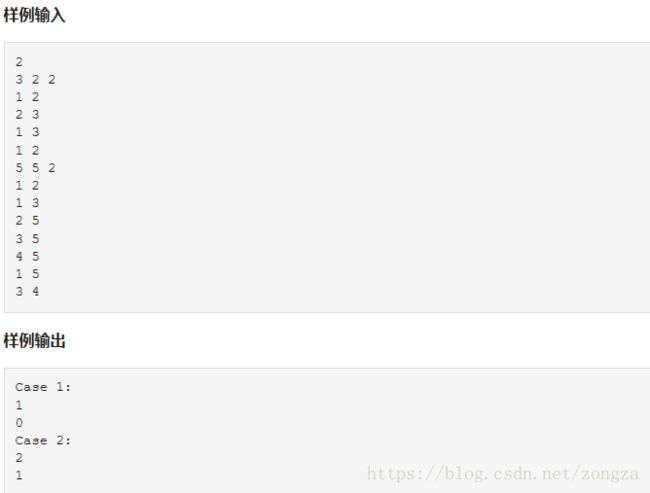
使用二维数组保存朋友关系
#include cin>>x>>y;
friends[x][y]=1;
friends[y][x]=1;
}
cout<<"Case "<":"<for(int i=0;icin>>x>>y;
int ans=0;
//访问数组检查朋友关系
for(int i=1;i<=n;i++)
if(friends[x][i]==1&&friends[y][i]==1) ans++;
cout<return 0;
}
12.5 哈夫曼树
//定义
priority_queue<long long,vector<long long>, greater<long long> > q;
// 读入数据
q.push(data);
//合并
while(q.size()>1)//堆中数据大于两个才能和并
{
int x = q.top();//堆顶
q.pop();
int y = q.top();
q.pop();
q.push(x+y);
带权路径长度+=(x+y);
}12.6 满二叉树的搜索
满二叉树的性质:
1 每层节点数= 2^层数
2 总的节点数=2^(层数+1) -1
3 左孩子=2*n ; 右孩子=2*n+1
4 父亲 = 左孩子/2=右孩子/2
//输入 总结点n, 当前节点m
int layer=1;
//处理中间行
while(2*m+1<=n)//右孩子小于等于终结点
{
ans+=pow(2,layer++);
m=2*m+1;
mm=2*mm;
}
//处理最后一行
if(n>=mm*2) ans+=((n-mm*2)+1);//输入 节点x 节点y
while(x!=y)
{
int temp = max(x,y);
int temp2= min(x,y);
y= temp/2;
x= temp2;
}第十三章 - 图
13.1 连通块(类似草丛问题) 点权W[MAX] 边权 G[MAX][MAX]
#include
#includeif(!visit[i])
{
团伙数++;//类似草丛数++
当前团伙头目=i;
当前团伙总人数=0;
当前团伙总边权=0;
DFS(i);//遍历一次后得到当前团伙的三个指标
if(当前团伙总人数>2&&当前团伙总边权>阈值)
头目->人数[当前团伙头目] = 当前团伙总人数;
}
}
void DFS(int 遍历的当前团伙成员)
{
//检查
if(visit[遍历的当前团伙成员]) return ;
//访问
visit[遍历的当前团伙成员]=1;
当前团伙总人数++;
if(W[遍历的当前团伙成员]>W[当前团伙头目]) 当前团伙头目=遍历的当前团伙成员;
//遍历(草丛是向四个方向遍历,连通块则是向所有可达方向遍历,可达方向可能有多个)
for(int i=0;i<所有人数;i++)
{
if(可达)//G[遍历的当前团伙成员][i]>0
{
当前团伙总边权+=G[遍历的当前团伙成员][i];
G[遍历的当前团伙成员][i]=G[i][遍历的当前团伙成员]=0;//删掉这条边防止回头
DFS(i);
}
}
} 13.2 最小生成树(包含全部点同时边权和最少)
bian B[MAX] ; //边表 kruskal的访问控制对象
int father[MAX]; //并查集 kruskal的更新对象
kruskal(int 总边数,int 总点数) 表示总点数总边数为x情况下生成树的最小边权和
//定义自己的边节点
struct bian
{
int 头,尾;
int 边权;
}B[MAX];
//输入点数n 边数m
int kruskal()
{
sort(边表B);
初始化并查集;
//枚举所有边
for(int i=0;i<边数;i++)
{
//得到边头与边尾的father findfather(B[i].边头); 函数定义参考并查集
if(边头f!=边尾f)
{
father[边尾]=边头;
边权和+=当前边边权;
当前边总数++;
if(当前边总数==点数-1) break;
}
}
//检查
if(当前边总数!=n-1) return -1;//说明无法连通
else return 当前边总数;
}kruskal算法
#includeint findfather(int a)
{
int temp=a;
//查找
while(a!=father[a]) a=father[a];
//优化压缩路径
while(temp!=father[temp])
{
int t_temp=temp;
temp=father[temp];
father[t_temp]=a;
}
//返回根节点
return a;
}
int kruskal(int num_p,int num_r)
{
//初始化
sort(R,R+num_r,cmp);
for(int i=0;iint costs=0;
int num_roads=0;
//从最小边开始查找和加入并查集
for(int i=0;i//查找
int FaA=findfather(R[i].shou);
int FaB=findfather(R[i].wei);
//加入
if(FaA!=FaB)
{
father[FaB]=FaA;
costs+=R[i].cost;
num_roads++;
}
//函数出口,结果检查
if(num_roads>=num_p-1) return costs;
}
}
int CHARtoINT(char a)
{
return int(a-'A');
}
int main()
{
//freopen("input.txt","r",stdin);
int n;
while(cin>>n&&n!=0)
{
int k=-1;//边的个数
for(int i=0;i1;i++)
{
char villy;cin>>villy;int tag = CHARtoINT(villy);
int num;cin>>num;
for(int j=0;jchar temp;cin>>temp;int tag2 = CHARtoINT(temp);
int value;cin>>value;
R[++k].shou=tag;R[k].wei=tag2;R[k].cost=value;//更新边表
}
}
int costs=kruskal(n,k+1);
cout<return 0;
} 13.3 dijstra单源点最短路径
PAT 1030 Travel Plan (有多种类型的边权 边长度,边花费)

dis[MAX]; //最短距离 dijstra的更新对象
visit[MAX]; //是否已经访问 dijstra的访问控制对象
G[MAX][MAX]; //边权 dijstra的访问控制对象
vector pre[MAX]; //最短路径中的前一节点 dijstra的更新对象
dian B[MAX] ; //点 用来更新G[MAX][MAX] (如subway,只告诉点坐标没告诉点与点间边权,要先把点保存起来)
dijkstra(int 起点) 表示更新从起点出发到其他点的最短距离dis[]
//初始化fill G[][]和 cost[][]为INF
//输入 G[][]和 cost[][]
//定义 int dis[]; bool vis[]; vector pre[] ;用于 dijkstra
void dijkstra(int start)
{
//初始化 d[]为INF ,vis[]为false;
dis[start]=0;
//以下操作for循环点数那么多次
//找到距离当前点最近的一个点并攻占
int index=-1;int min_dis = INF;
for(int i=0;i<点数;i++)
{
if(dis[i]0)
{
index=i;
min_dis=dis[i];
}
}
if(index==-1) return ;//该点与其他点不是连通的
visit[index]=1;
//从找到的最近点出发更新dis
for(int i=0;i<点数;i++)
{
if(G[index][i]!=INF && visit[i]==0 )
{
if(dis[i]>dis[index]+G[index][i])
{
dis[i]=dis[index]+G[index][i];
pre[i].clear();
pre[i].push_back(index);
}
else if(dis[i]==dis[index]+G[index][i])
pre[i].push_back(index);
}
}
}
//定义 vector temp_path,path; 用于递归求解最佳路径(如果带有多个标尺)
void dfs(int end)
{
//出口
if(end == start)
{
temp_path.push_back(end);
//计算temp_path里的边权和 倒着访问
//for(int i = temp_path.size()-1;i>0;i--) temp_cost+=G[ temp_path[i] ][ temp_path[i-1] ];
//更新最小边权和与路径 mincost=min();path= temp_path;
temp_path.pop_back();
return ;
}
temp_path.push_back(end);
//遍历所有能到的上一个节点
//for(int i=0;i
temp_path.pop_back();
}
//path,mincost为所求 2502 Subway (边权没有直接给你而是经过计算得到) 边的输入较为繁琐

#include//找到离当前点最近的点下标并攻占
double minn=INF;//注意double型
for( j=1 ; j<=n ; j++)
{
if(!vis[j] && minn>dis[j] )
{
minn=dis[j];
u=j;
}
}
vis[u]=1;
//从找到的点出发更新dis
for( j=1 ; j<=n ; j++ )
if(!vis[j]&&Map[u][j]!=INF&& dis[j] > dis[u]+Map[u][j])
dis[j]=dis[u]+Map[u][j];
}
printf("%.0f",dis[2]);
}
double feet(Point t,Point s)
{
return sqrt((t.x-s.x)*(t.x-s.x)+(t.y-s.y)*(t.y-s.y));//两点之间距离
}
int main()
{
int i,j,k=3;//k现在赋值第一条地铁的首个地铁站
for( i=1 ; ifor( j=1 ; jif(i==j)
Map[i][j] = 0 ;
else
Map[i][j] = INF ;
scanf("%d%d%d%d",&dkr[1].x ,&dkr[1].y,&dkr[2].x ,&dkr[2].y);//起点,终点
n=3;
int x,y;
while(~scanf("%d%d",&x,&y))//地铁
{
if(x==-1&&y==-1)
{
k=n;
continue;
}
dkr[n].x=x;
dkr[n].y=y;
//先用地铁速度更新地铁线上的点的G[][]
if(n!=k)//本条地铁的首个站点不能与相邻地铁站建边
Map[n][n-1]=Map[n-1][n]=feet(dkr[n],dkr[n-1])*3/2000;
n++;
}
//再用步行速度更新所有点的min(G[][])
for( i=1 ; i<=n ;i++)//步行
{
for( j=1 ; j<=n ; j++ )
Map[i][j]=Map[j][i]=min(Map[i][j],feet(dkr[i],dkr[j])*3/500);
}
dijkstra(1);
return 0;
}