数字图像处理相关题目解析(直方图均衡化、中值滤波、邻域平均、霍夫曼编码)
1.什么是图像?模拟图像与数字图像有什么区别?
答:(1)图像是对客观对象的一种相似性的.生动性的描述或写真。或者说图像是客观对象的一种表示,它包含 了被描述对象的有关信息。它是人们最主要的信息源。
(2)按图像空间坐标和亮度(或色彩)的连续性可分为模拟图像和数字图像。模拟图像指空间坐标和亮度(或色彩)都是连续变化的图像。模拟图像可用连续函数来描述。数字图像是一种空间坐标和灰度均不连续的用离散数字(一般用整数)表示的图像。数字图像可用矩阵或数组来描述。
2.模拟图像处理与数字图像处理的主要区别表现在哪些地方?
答:利用光学、照像方法对模拟图像的处理称为模拟图像处理。所谓数字图像处理,就是利用计算机对数字图像进行系列操作,从而获得某种预期的结果的技术。数字图像处理离不开计算机,因此又称计算机图像处理。
主要区别表现:
① 数学描述方法:模拟图像主要用连续数学方法,数字图像主要用离散数学方法。
② 图像分辨率表示:数字图像分辨率是指反映整个图像画面垂直和水平方向像素数乘积。模拟图像分辨率是指反映整个画面最多的扫描线数。
③ 图像处理:数字图像是通过对模拟图像采样,量化等处理获得的,模拟图像处理的方式很少,往往只能进行简单的放大、缩小等,而数字图像的处理方式可以非常精确、灵活。数字图像处理再现性好,模拟图像的保存性较差,时间长了会有所变化,而数字图像不会因为保存、传输或复制而产生图像质量上的变化。但数字图像处理速度较慢,存储容量大。
④ 图像传输:模拟图像以实物为载体,传输相对困难,而数字图像以数字信息为载体,传输相对较快。

解: v 0 = 5 64 v_0=\frac{5}{64} v0=645 v 1 = 12 64 v_1=\frac{12}{64} v1=6412 v 2 = 16 64 v_2=\frac{16}{64} v2=6416 v 3 = 8 64 v_3=\frac{8}{64} v3=648 v 4 = 1 64 v_4=\frac{1}{64} v4=641 v 5 = 7 64 v_5=\frac{7}{64} v5=647 v 6 = 10 64 v_6=\frac{10}{64} v6=6410 v 7 = 5 64 v_7=\frac{5}{64} v7=645
图像信息熵H(熵): H = − ∑ i = 0 n − 1 P i l o g 2 P i = − ( 5 64 × l o g 2 5 64 + 12 64 × l o g 2 12 64 + 16 64 × l o g 2 16 64 + 8 64 × l o g 2 8 64 + 1 64 × l o g 2 1 64 + 7 64 × l o g 2 7 64 + 10 64 × l o g 2 10 64 + 5 64 × l o g 2 5 64 ) = 2.76 H=- \sum_{i=0}^{n-1}P_i log_2P_i =-(\frac{5}{64}×log_2\frac{5}{64}+\frac{12}{64}×log_2\frac{12}{64}+\frac{16}{64}×log_2\frac{16}{64}+\frac{8}{64}×log_2\frac{8}{64}+\frac{1}{64}×log_2\frac{1}{64}+\frac{7}{64}×log_2\frac{7}{64}+\frac{10}{64}×log_2\frac{10}{64}+\frac{5}{64}×log_2\frac{5}{64} )=2.76 H=−∑i=0n−1Pilog2Pi=−(645×log2645+6412×log26412+6416×log26416+648×log2648+641×log2641+647×log2647+6410×log26410+645×log2645)=2.76

14.什么是小波?小波函数是惟一的吗?
答: “小波”就是小的波形。所谓“小”是指它具有衰减性;而称之为“波”则是指它的波动性,其振幅呈正负相间的震荡形式。
小波函数的选择既不是惟一的,也不是任意的。
15.一个小波函数应满足哪些容许性条件?
答:(1)定义域应是紧支撑的,即在一个很小的区间外,函数为零,也就是函数应有速降特性。
(2)平均值为零,即
∫ − ∞ + ∞ φ ( t ) d t = 0 ∫_{-∞}^{+∞}φ(t)dt=0 ∫−∞+∞φ(t)dt=0
,其高阶矩阵也为零。
∫ − ∞ + ∞ t k φ ( t ) d t = 0 , 其 中 k = 0 , 1 , 2 , … , N − 1 ∫_{-∞}^{+∞}t^k φ(t)dt=0 ,其中 k=0,1,2,…,N-1 ∫−∞+∞tkφ(t)dt=0,其中k=0,1,2,…,N−1
该条件也叫小波的容许条件。

分析:
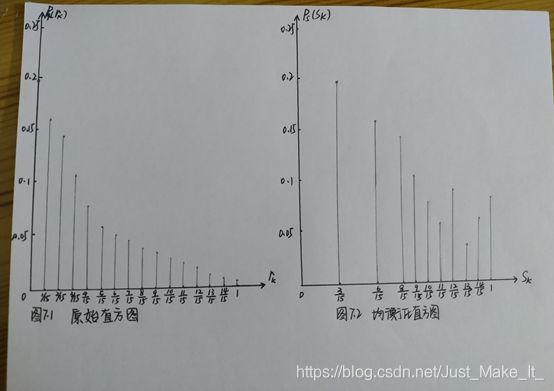
①计算 S k S_k Sk计:
S k S_k Sk计 = ∑ j = 0 j P =\sum_{j=0}^{j}P =∑j=0jPr(rj)
例如: S 1 S_1 S1计 = ∑ j = 0 1 P =\sum_{j=0}^{1}P =∑j=01Pr(rj) = 0.195 + 0.160 = 0.355 =0.195+0.160=0.355 =0.195+0.160=0.355
②计算 S k S_k Sk并:采用4舍5入的方法对 S k S_k Sk计加以修饰。
例如:当 S k S_k Sk计等于0.195时,四舍五入最接近 3 15 \frac{3}{15} 153,故 S k S_k Sk并 = 3 15 =\frac{3}{15} =153。
③输出图像的灰度级 S k S_k Sk,即10个级别。
④计算对应每个 S k S_k Sk的 n s n_s nsk
例如:当 S k S_k Sk等于1时, n s n_s nsk = 96 + 80 + 70 + 50 + 30 = 326 =96+80+70+50+30=326 =96+80+70+50+30=326
⑤计算 P s P_s Psk ( S k ) = (S_k)= (Sk)= n s k n \frac{n_sk}{n} nnsk,在这里有一个简单的计算,以计算 S k S_k Sk等于1时为例: P s P_s Psk ( S k ) = 0.023 + 0.019 + 0.017 + 0.012 + 0.07 = 0.078 (S_k)=0.023+0.019+0.017+0.012+0.07=0.078 (Sk)=0.023+0.019+0.017+0.012+0.07=0.078,即对所有 S k S_k Sk并 = 1 =1 =1的 P r ( r k ) P_r(r_k) Pr(rk)求和。
解:

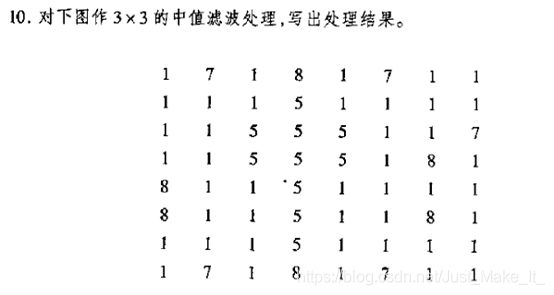
分析:本题是8×8的矩阵做3×3的中值滤波处理,首先边缘部分保持不变,用中值代替窗口中心像素的原来灰度值。
具体步骤:

对红色线框里面数字进行排序1 1 1 1 1 1 1 5 7,中值为1,即用中值数1替换红色线框中心的数字1。

对于此红色线框中3×3矩阵,进行相同的步骤,先排序1 1 1 1 5 5 5 7 8,选取中值数为5,即用5替换红色线框中心的数字1。
以此类推。
解:中值滤波处理最终结果如下
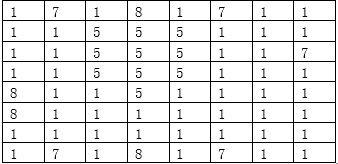
11.对上图作3×3的邻域平均,并比较邻域平均与中值滤波的差异。
分析:解题过程同上。
解:邻域平均处理结果如下

中值滤波与领域平均的差异:①领域平均算法简单,但它的主要缺点是在降低噪声的同时使图像产生模糊,特别在边缘和细节处。而且邻域越大,在去噪能力增强的同时模糊程度越严重。②中值滤波是对一个滑动窗口内的诸像素灰度值排序,用中值代替窗口中心像素的原来灰度值,因此它是一种非线性的图像平滑法。它对脉冲干扰及椒盐噪声的抑制效果好,在抑制随机噪声的同时能有效保护边缘少受模糊。但它对点、线等细节较多的图像却不太合适。

分析:
①编码的时候从右往左开始编码,相对好理解一些。下一个编码一部分都是在上一个编码的基础上产生出来的。
②用二叉树进行霍夫曼编码算法步骤如下:
Step1.统计每个元素出现的频率(该题已经给出);
Step2.将频率从左到右按照从大到小的顺序排列;
Step3.选出频率最小的两个值,作为二叉树的两个叶子节点,将其和作为它们的根节点,两个叶子节点不再参与排序,新的根节点同其余元素出现的频率排序。
Step4.重复Step3,直到最后得到和为1的根节点。
Step5.将形成的二叉树的子节点左边标0,右边标1。把最上面的根节点到最下面的叶子节点途中遇到的0,1序列串起来,就得到了各个元素的编码。
解:

信源的熵: H = − ∑ i = 1 8 P i l o g 2 P i = − [ 0.20 × l o g 2 ( 0.20 ) + 0.09 × l o g 2 ( 0.09 ) + 0.11 × l o g 2 ( 0.11 ) + 0.13 × l o g 2 ( 0.13 ) + 0.07 × l o g 2 ( 0.07 ) + 0.12 × l o g 2 ( 0.12 ) + 0.08 × l o g 2 ( 0.08 ) + 0.20 × l o g 2 ( 0.20 ) ] = 2.9 H=- ∑_{i=1}^{8}P_i log_2P_i =-[0.20×log_2(0.20)+0.09×log_2(0.09)+0.11×log_2(0.11)+0.13×log_2(0.13)+0.07×log_2(0.07)+0.12×log_2(0.12)+0.08×log_2(0.08)+0.20×log_2(0.20) ]=2.9 H=−∑i=18Pilog2Pi=−[0.20×log2(0.20)+0.09×log2(0.09)+0.11×log2(0.11)+0.13×log2(0.13)+0.07×log2(0.07)+0.12×log2(0.12)+0.08×log2(0.08)+0.20×log2(0.20)]=2.9
平均码长: B ‾ = ∑ i = 1 8 P ( w i ) β i = 0.2 × 2 + 0.09 × 4 + 0.11 × 4 + 0.13 × 3 + 0.07 × 4 + 0.12 × 3 + 0.08 × 4 + 0.2 × 2 = 2.95 \overline{B}=∑_{i=1}^{8}P(w_i ) β_i=0.2×2+0.09×4+0.11×4+0.13×3+0.07×4+0.12×3+0.08×4+0.2×2=2.95 B=∑i=18P(wi)βi=0.2×2+0.09×4+0.11×4+0.13×3+0.07×4+0.12×3+0.08×4+0.2×2=2.95
编码效率: r = H B ‾ − 1 = 2.95 2.9 − 1 = 1.72 % r=\frac{H}{\overline{B}} -1=\frac{2.95}{2.9}-1=1.72\% r=BH−1=2.92.95−1=1.72%
冗余度: η = B ‾ H = 1 r + 1 = 98.3 % η=\frac{\overline{B} }{H}=\frac{1}{r+1}=98.3\% η=HB=r+11=98.3%
