分门别类刷leetcode——递归和回溯搜索(C++实现)
基础复习
回溯法
leetcode 78 子集
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[[3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], []]思路:
方法一——回溯法
class Solution {
public:
void generate(int i, vector&nums, vector&item, vector>&result){
if(i>=nums.size()) return;
item.push_back(nums[i]);
result.push_back(item);
//放i的结果
generate(i+1,nums,item,result);
item.pop_back();
//不放i的结果
generate(i+1, nums, item, result);
}
vector> subsets(vector& nums) {
vector>result;
vectoritem;
result.push_back(item);
generate(0,nums,item,result);
return result;
}
};
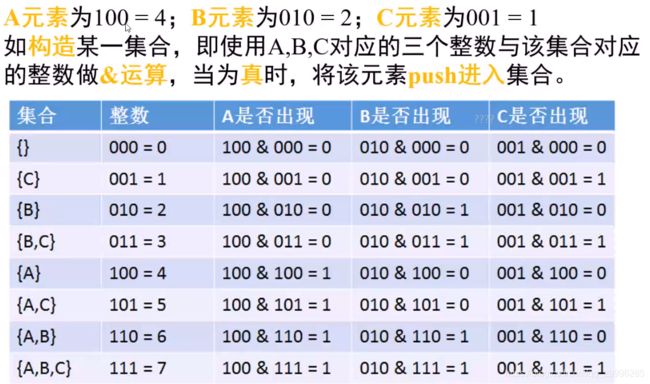
方法二——位运算
每个元素都有放和不放两种决策。因此一共八种情况。针对每一种情况,依次判断每个元素是否在该集合中出现。
class Solution {
public:
vector> subsets(vector& nums) {
vector>result;
int all_set=1<item;
//A 100 即 1<<2, B 010 即 1<<1, C 001 即 1<<0
for(int j=0; j
leetcode 90 子集 II
给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: [1,2,2]
输出:
[ [2], [1], [1,2,2], [2,2], [1,2], []]思路:
使用上题的方法获取所有子集之后,使用set去重。
class Solution {
public:
vector> subsetsWithDup(vector& nums) {
sort(nums.begin(),nums.end());
vector>result;
int all_set=1<item;
//A 100 即 1<<2, B 010 即 1<<1, C 001 即 1<<0
for(int j=0; j>con;
for(auto i : result){
con.insert(i);
}
result.clear();
for(auto i :con){
result.push_back(i);
}
return result;
}
};
leetcode 40 组合总和 II
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明:
- 所有数字(包括目标数)都是正整数。
- 解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[ [1, 7], [1, 2, 5], [2, 6], [1, 1, 6] ]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[ [1,2,2], [5] ]思路:
将数组排序,然后分别考虑每一个元素是否加入到集合,每个元素都有加入集合和不加入集合这两种可能。用一个变量sum来累计集合中的各个元素的总和。使用set来进行去重。
class Solution {
public:
void generate(int i, vector&nums, vector>&result, vector&item,
set>&res_set, int sum, int target){
if(i>=nums.size()||sum>target) return;//剪枝
//sum为当前自己item中的元素和
sum+=nums[i];
item.push_back(nums[i]);
if(target==sum && res_set.find(item)==res_set.end()){
result.push_back(item);
res_set.insert(item);
}
//放i且sum小于target的时候
generate(i+1, nums, result, item, res_set, sum, target);
sum-=nums[i];
item.pop_back();
//不i且sum小于target的时候
generate(i+1, nums, result, item, res_set, sum, target);
}
vector> combinationSum2(vector& candidates, int target) {
sort(candidates.begin(), candidates.end());
set>res_set;
vectoritem;
vector>result;
generate(0, candidates, result, item, res_set, 0, target);
return result;
}
};
leetcode 22 括号生成
给出 n 代表生成括号的对数,请你写出一个函数,使其能够生成所有可能的并且有效的括号组合。
例如,给出 n = 3,生成结果为:
[ "((()))", "(()())", "(())()", "()(())", "()()()" ]思路:
n组括号,字符串长度为2的n次幂,字符串中每个字符都有两种选择,“(”或者“)”。因此有2*(2的n次幂种) 种可能。
放置的时候,如果当前右括号的数量超过左括号,则该组合不合法。
class Solution {
public:
vector generateParenthesis(int n) {
vectorresult;
generate("", n, n, result);
return result;
}
private:
void generate(string item, int left, int right,
vector&result){
//左右括号都放完了,此时递归结束
if(left==0 && right==0){
result.push_back(item);
return;
}
if(left){
generate(item+'(',left-1, right, result);
}
//保证括号的合法性
if(left
leetcode 51 N皇后
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
上图为 8 皇后问题的一种解法。
给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例:
输入: 4
输出: [
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。思路:
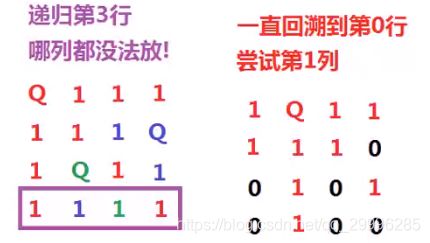
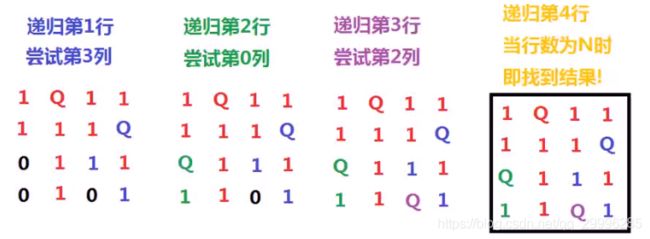
四个皇后的回溯摆放过程:
class Solution {
public:
void put_down_the_queen(int x, int y, vector>&mark){
//方向数组,分别代表 左,右,下,上,左下,左上,右下和右上
static const int dx[]={-1,1,0,0,-1,-1,1,1};
static const int dy[]={0,0,-1,1,-1,1,-1,1};
mark[x][y]=1;//皇后的位置(x,y)
//给八个位置都打上1,标记为后续不能放置皇后的位置
for(int i=1; i=0 && new_x =0 && new_y&location,
vector>&result, vector>&mark){
//完成了所有皇后的放置任务
if(k==n){
result.push_back(location);
return;
}
//按顺序尝试第0到第n-1列
for(int i=0; i>temp_mark=mark;
//记录当前皇后位置
location[k][i]='Q';
//把八个方向做出标记,以后这些位置就不能放皇后了
put_down_the_queen(k,i,mark);
//考虑第k+1个皇后的放置方式
generate(k+1, n, location, result, mark);
//说明下一行放置不成功,将mark重置为回溯前的状态
mark=temp_mark;
//该位置不能放皇后,改为 .
location[k][i]='.';
}
}
}
vector> solveNQueens(int n) {
vector>result;
vector>mark;
vectorlocation;
//初始化一个 n*n的 . 表格
for(int i=0; i());
for(int j=0; j
leetcode 473 火柴拼正方形
还记得童话《卖火柴的小女孩》吗?现在,你知道小女孩有多少根火柴,请找出一种能使用所有火柴拼成一个正方形的方法。不能折断火柴,可以把火柴连接起来,并且每根火柴都要用到。
输入为小女孩拥有火柴的数目,每根火柴用其长度表示。输出即为是否能用所有的火柴拼成正方形。
示例 1:
输入: [1,1,2,2,2]
输出: true
解释: 能拼成一个边长为2的正方形,每边两根火柴。
示例 2:
输入: [3,3,3,3,4]
输出: false
解释: 不能用所有火柴拼成一个正方形。
注意:
- 给定的火柴长度和在
0到10^9之间。 - 火柴数组的长度不超过15。
方法一(回溯):
如果传入的数组中的元素个数小于4或者数组总和并不能被4整除,则说明数组拼不出正方形。
调用递归函数,以数组总和的1/4作为目标值,回溯尝试每一个元素。
每一根火柴也有两种情况,放入该边上或者不放入该边上。
class Solution {
public:
bool generate(int i, vector&nums, int target, int bucket[]){
//说明数组中的元素考察完毕
if(i>=nums.size()){
return bucket[0]==target && bucket[1]==target
&& bucket[2]==target && bucket[3]==target;
}
for(int j=0; j<4; j++){
//说明该组合超过了正方形的边长
if(bucket[j]+nums[i]>target) continue;
bucket[j]+=nums[i];
//此次递归的结果返回值为true
if(generate(i+1, nums, target, bucket)){
return true;
}
//此次递归的结果返回值为false,将最后一个元素的值减去,考虑下一个元素的值
bucket[j]-=nums[i];
}
return false;
}
bool makesquare(vector& nums) {
if(nums.size()<4) return false;
int sum=0;
for(auto i:nums){
sum+=i;
}
if(sum%4!=0) return false;
//从大到小排序
sort(nums.rbegin(), nums.rend());
int bucket[4]={0};
return generate(0, nums, sum/4, bucket);
}
};
方法二(位运算):
class Solution {
public:
bool makesquare(vector& nums) {
if(nums.size()<4) return false;
int sum=0;
for(auto i:nums)
sum+=i;
if(sum%4) return false;
int target=sum/4;
vectorok_subset;
vectorok_half;
int all=1<