复变函数-复数的基本知识
文章目录
- 复数的概念及运算
- 定义
- 四则运算
- 共轭复数
- 定义
- 性质
- 复数的表示方法
- (1)点的表示
- (2)向量表示法
- (3)三角表示
- (4)指数表示法
- 复球面
- 定义
- 扩充复平面
- 定义
- 关于 $\infty$ 的四则运算
复数的概念及运算
定义
z = x + i y z=x + i y z=x+iy
∣ z ∣ = x 2 + y 2 |z|=\sqrt{x^2+y^2} ∣z∣=x2+y2
其中 x x x 和 y y y 是实数, i i i是虚单位 ( i 2 = − 1 i^2=-1 i2=−1 ), 称为复数
其中 x x x 和 y y y 分别称为复数 z z z 的实部和虚部,分别记作:
- x = R e z x=Re z x=Rez
- y = I m z y=Im z y=Imz
两个复数相等是指它们的实部与虚部分别相等
如果 I m z = 0 Im z= 0 Imz=0,那么称 z z z为一个实数;
如果 I m z ≠ 0 Im z\neq\ 0 Imz= 0,那么称 z z z为一个虚数;
如果 I m z ≠ 0 Im z\neq\ 0 Imz= 0,而 R e z = 0 Re z=0 Rez=0,那么称 z z z为一个纯虚数
四则运算
已知:
z 1 z_1 z1= x 1 x_1 x1+ i y 1 iy_1 iy1
z 2 z_2 z2= x 2 x_2 x2+ i y 2 iy_2 iy2
和差: z 1 ∓ z 1 z_1\mp\ z_1 z1∓ z1= ( x 1 ∓ x 2 ) ∓ i ( y 1 ∓ y 2 ) (x_1\mp\ x_2)\mp\ i(y_1\mp\ y_2) (x1∓ x2)∓ i(y1∓ y2)
复数的加减是向量的加减
积: z 1 z 2 z_1z_2 z1z2= ( x 1 x 2 − y 1 y 2 ) + i ( x 1 y 2 + x 2 y 1 ) (x_1x_2-y_1y_2)+i(x_1y_2+x_2y_1) (x1x2−y1y2)+i(x1y2+x2y1)
商: z 1 z 2 \frac{z_1}{z_2} z2z1= x 1 x 2 + y 1 y 2 x 2 2 + y 2 2 + i x 2 y 1 − x 1 y 2 x 2 2 + y 2 2 \frac{x_1x_2+y_1y_2}{x^2_2+y^2_2}+i\frac{x_2y_1-x_1y_2}{x^2_2+y^2_2} x22+y22x1x2+y1y2+ix22+y22x2y1−x1y2
共轭复数
定义
若 z = x + i y z=x+iy z=x+iy , 称 z ‾ = x − i y 为 z \overline{z}=x-iy为z z=x−iy为z的共轭复数
性质
( z 1 ∓ z 2 ‾ ) = ( z 1 ‾ ∓ z 2 ‾ ) (\overline{z_1\mp\ z_2})=(\overline{z_1}\mp\ \overline{z_2}) (z1∓ z2)=(z1∓ z2)
( z 1 z 2 ‾ ) = z 1 ‾ (\overline{z_1z_2})=\overline{z_1} (z1z2)=z1 z 2 ‾ \overline{z_2} z2
( z 1 z 2 ) ‾ = z 1 ‾ z 2 ‾ \overline{(\frac{z_1}{z_2})}=\frac{\overline{z_1}}{\overline{z_2}} (z2z1)=z2z1
z ‾ \overline{z} z 的共轭复数是 z z z
z z ‾ = R e ( z ) 2 + I m ( z ) 2 = x 2 + y 2 z\overline{z}=Re (z)^2+Im(z)^2=x^2+y^2 zz=Re(z)2+Im(z)2=x2+y2 可以推出 1 z = z ‾ ∣ z ∣ 2 \frac{1}{z}=\frac{\overline{z}}{|z|^2} z1=∣z∣2z
z + z ‾ = 2 R e ( z ) z+\overline{z}=2Re(z) z+z=2Re(z)
z − z ‾ = 2 i I m ( z ) z-\overline{z}=2iIm(z) z−z=2iIm(z)
复数的表示方法
(1)点的表示
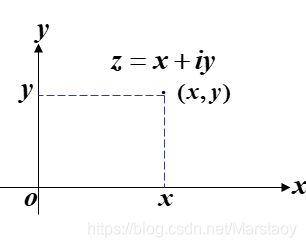
z = x + i y z=x+iy z=x+iy 与复平面上的点 ( x , y ) (x,y) (x,y)一一对应
做题要先画复平面
(2)向量表示法
z = x + i y 可 以 用 O P ⃗ = ( x , y ) 表 示 z=x+iy可以用\vec{OP}=(x,y)表示 z=x+iy可以用OP=(x,y)表示
向量的长度为复数 z = x + i y z=x+iy z=x+iy的模或绝对值
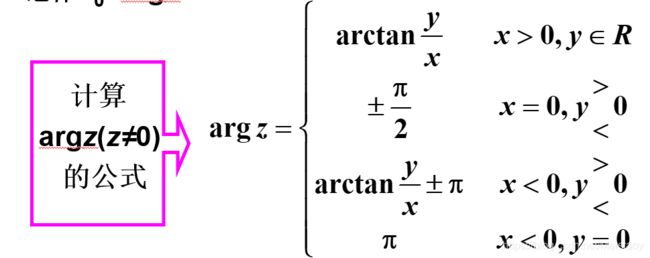
正实轴为始边(计算argz要记得他的起点是x轴正半轴) 以 O P ⃗ \vec{OP} OP 为终边的角的弧度数 称为复数 z = x + i y z=x+iy z=x+iy 的辐角
- 辐角一般表示: θ = A r g z \theta=Arg z θ=Argz
- 主辐角: θ = a r g z \theta=arg z θ=argz
其 中 θ 满 足 − π < θ ≤ π 或 者 0 ≤ θ < 2 π 的 θ 其中\theta满足 -\pi<\theta\le\pi 或者0\le\theta<2\pi 的θ 其中θ满足−π<θ≤π或者0≤θ<2π的θ
注意:
- z = 0 , z=0, z=0,辐角不确定
- z ≠ 0 , t a n = ( A r g ) z \neq\ 0,tan=(Arg) z= 0,tan=(Arg)
- 辐角无穷多: A r g z = θ = θ 0 + 2 k π , k ∈ Z , θ 0 为 辐 角 A r g z 的 主 值 Arg z=θ=θ_0+2kπ, k∈Z,\theta_0为辐角Argz的主值 Argz=θ=θ0+2kπ,k∈Z,θ0为辐角Argz的主值
- ∣ z 1 − z 2 ∣ 表 示 z 1 和 z 2 之 间 的 距 离 |z_1-z_2|表示z_1和z_2之间的距离 ∣z1−z2∣表示z1和z2之间的距离
(3)三角表示
z = x + i y = x 2 + y 2 ( x x 2 + y 2 + i y x 2 + y 2 ) z=x+iy=\sqrt{x^2+y^2}(\frac{x}{\sqrt{x^2+y^2}}+i\frac{y}{\sqrt{x^2+y^2}}) z=x+iy=x2+y2(x2+y2x+ix2+y2y)
由 { x = r c o s θ y = r s i n θ \begin{cases} x=rcos\theta\\ y=rsin\theta \end{cases} {x=rcosθy=rsinθ
可得 z = r ( c o s θ + i s i n θ ) z=r(cos\theta+isin\theta) z=r(cosθ+isinθ)
(4)指数表示法
由欧拉公式 e i θ = c o s θ + i s i n θ e^{i\theta}=cos\theta+isin\theta eiθ=cosθ+isinθ
可得 z = r e i θ z=re^{i\theta} z=reiθ

复球面
定义
球面上的点,(除去北极 N 外)与复平面内的点之间存在着一一对应的关系. 我们可以用球面上的点来表示复数.
我们规定: 复数中有一个唯一的“无穷大”与复平面上的无穷远点相对应, 记作 ∞ \infty ∞ .
因而球面上的北极 N 就是复数无穷大 ∞ \infty ∞ 的几何表示.
球面上的每一个点都有唯一的复数与之对应, 这样的球面称为复球面.
扩充复平面
定义
包括无穷远点在内的复平面称为扩充复平面
不包括无穷远点在内的复平面称为有限复平面, 或简称复平面
对于复数 来说, 实部,虚部,辐角等概念均无意义, 它的模规定为正无穷大
即 ∣ z ∣ = + ∞ |z|=+\infty ∣z∣=+∞
关于 ∞ \infty ∞ 的四则运算
加法: α + ∞ = ∞ + α = ∞ , ( α ≠ ∞ , 因 为 ∞ 有 两 个 方 向 ) \alpha+\infty=\infty+\alpha=\infty,(\alpha \neq\ \infty,因为\infty有两个方向) α+∞=∞+α=∞,(α= ∞,因为∞有两个方向)
减法: α − ∞ = ∞ − α = ∞ , ( α ≠ ∞ , 因 为 ∞ 有 两 个 方 向 ) \alpha-\infty=\infty-\alpha=\infty,(\alpha \neq\ \infty,因为\infty有两个方向) α−∞=∞−α=∞,(α= ∞,因为∞有两个方向)
乘法: α ⋅ ∞ = ∞ ⋅ α = ∞ , ( α ≠ 0 ) \alpha\cdot\infty=\infty\cdot\alpha=\infty,(\alpha \neq\ 0) α⋅∞=∞⋅α=∞,(α= 0)
除法: α ∞ = 0 , ∞ α = ∞ , ( α ≠ ∞ ) α 0 = ∞ ( α ≠ 0 ) \frac{\alpha}{\infty}=0,\frac{\infty}{\alpha}=\infty,(\alpha \neq\ \infty)\frac{\alpha}{0}=\infty(\alpha \neq\ 0) ∞α=0,α∞=∞,(α= ∞)0α=∞(α= 0)