计算机指令与运算基础原理笔记
一、汇编代码与指令
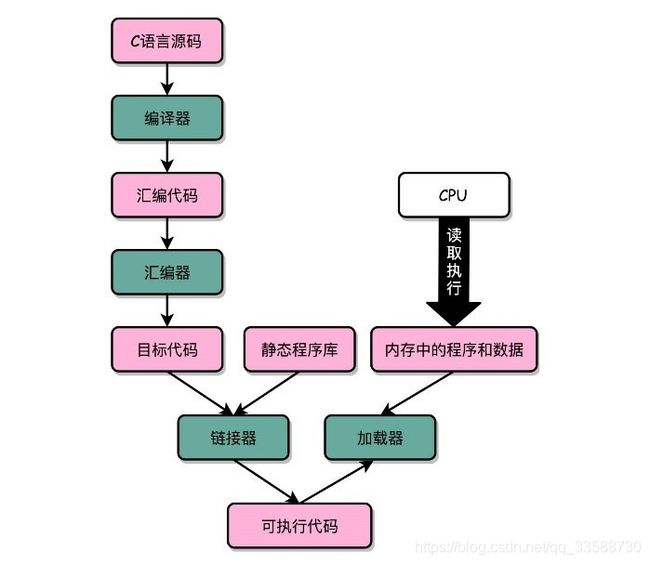
1.要让程序在一个 Linux 操作系统上跑起来,需要把整个程序翻译成汇编语言(ASM,Assembly Language)的程序,这个过程叫编译(Compile)成汇编代码。针对汇编代码,可以再用汇编器(Assembler)翻译成机器码(Machine Code)。这些机器码由“0”和“1”组成的机器语言表示。这一条条机器码,就是一条条的计算机指令。这样一串串的 16 进制数字,就是 CPU 能够真正认识的计算机指令。在一个 Linux 操作系统上,可以使用 gcc 和 objdump 这样两条命令,把C语言文件test.c对应的汇编代码和机器码都打印出来:
gcc -g -c test.c
$ objdump -d -M intel -S test.o在命令输出中,左侧有一堆数字,这些就是一条条机器码;右边有一系列的 push、mov、add、pop 等,这些就是对应的汇编代码。一行 C 语言代码,有时候只对应一条机器码和汇编代码,有时候则是对应两条机器码和汇编代码。汇编代码和机器码之间是一一对应的,如下所示:
test.o: file format elf64-x86-64
Disassembly of section .text:
0000000000000000 :
int main()
{
0: 55 push rbp
1: 48 89 e5 mov rbp,rsp
int a = 1;
4: c7 45 fc 01 00 00 00 mov DWORD PTR [rbp-0x4],0x1
int b = 2;
b: c7 45 f8 02 00 00 00 mov DWORD PTR [rbp-0x8],0x2
a = a + b;
12: 8b 45 f8 mov eax,DWORD PTR [rbp-0x8]
15: 01 45 fc add DWORD PTR [rbp-0x4],eax
}
18: 5d pop rbp
19: c3 ret
汇编代码其实就是“给程序员看的机器码”,也正因为如此,机器码和汇编代码是一一对应的。程序员很容易记住add、mov这些用英文表示的指令,而8b 45 f8这样的指令,由于很难一下子看明白是在干什么,所以会非常难以记忆。
常见的指令可以分成五大类:
(1)算术类指令,如加减乘除。(2)数据传输类指令,如给变量赋值、在内存里读写数据等。(3)逻辑类指令,如逻辑上的与或非。(4)条件分支类指令,如“if/else”。(5)无条件跳转指令,如写一些大一点的程序,常常需要写一些函数或者方法。在调用函数的时候,其实就是发起了一个无条件跳转指令。在汇编语言中这五类指令的体现如下所示:
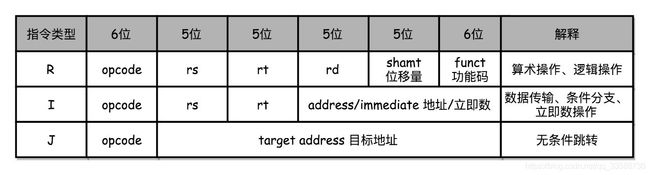
2.为了理解机器码的计算方式,以CPU指令集中相对简单的MIPS指令集为例,MIPS的指令是一个32位整数,高6位叫操作码(Opcode),代表这条指令具体是一条什么样的指令,剩下的26位有三种格式,分别是R、I和J:
(1)R指令是一般用来做算术和逻辑操作,里面有读取和写入数据的寄存器的地址。如果是逻辑位移操作,后面还有位移操作的位移量,而最后的功能码,则是在前面的操作码不够的时候,扩展操作码表示对应的具体指令。
(2)I指令通常用在数据传输、条件分支,以及在运算时使用的是常数的情况。这个时候,没有了位移量和操作码,也没有了第三个寄存器,而是把这三部分直接合并成了一个地址值或者一个常数。
(3)J指令就是一个跳转指令,高 6 位之外的 26 位都是一个跳转后的地址。
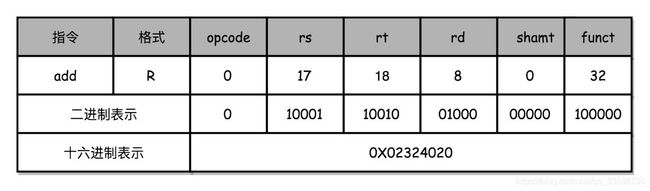
例如汇编代码add $t0, $s2, $s1,对应的MIPS指令里opcode是0,假设rs代表第一个寄存器s1的地址是17,rt代表第二个寄存器s2的地址是18,rd代表目标的临时寄存器t0的地址是8。因为不是位移操作,所以位移量是0。把这些数字拼在一起,就变成了一个 MIPS 的加法指令,如下所示:
真正的机器码是二进制,但为了避免显示过长的数字,因此理解例子时用十六进制来表示一条机器码,所以该例子中0X02324020就是这条指令对应的机器码(从右到左每4个二进制位为1个十六进制位),对于几十年前的打孔纸带计算机来说,如果在对应位置用打孔代表1,没有打孔代表0,用4行8列代表一条指令来打一个穿孔纸带,每一列都是一个二进制表示,那么这条指令产生的打孔纸带是这样的:
除了C这样的编译型语言之外,不管是Python这样的解释型语言,还是Java这样使用虚拟机的语言,最终都是由不同形式的程序,把写好的代码转换成CPU能够理解的机器码来执行,只不过解释型语言是通过解释器在程序运行的时候逐句翻译,而Java这样使用虚拟机的语言,则是由虚拟机对编译出来的中间代码进行解释,或者即时编译成为机器码来最终执行。
二、指令跳转
3.从逻辑上看,CPU实际上由一堆寄存器组成,而寄存器就是CPU内部,由多个触发器(Flip-Flop)或者锁存器(Latches)组成的简单电路,这是两种不同原理的数字电路组成的逻辑门。N个触发器或者锁存器,就可以组成一个N位(Bit)的寄存器,能够保存N位的数据。比方说64位Intel的CPU,寄存器就是64位的。
一个CPU里面会有很多种不同功能的寄存器,比较重要的有三种:
(1)PC 寄存器(Program Counter Register),也叫指令地址寄存器(Instruction Address Register),用来存放下一条需要执行的计算机指令的内存地址。
(2)指令寄存器(Instruction Register),用来存放当前正在执行的指令。
(3)条件码寄存器(Status Register),用里面的一个一个标记位(Flag),存放CPU进行算术或者逻辑计算的结果。
除了这些特殊的寄存器,CPU里面还有更多用来存储数据和内存地址的寄存器。这样的寄存器通常一类里面不止一个。通常根据存放的数据内容来给它们取名,比如整数寄存器、浮点数寄存器、向量寄存器和地址寄存器等等。有些寄存器既可以存放数据,又能存放地址,就叫通用寄存器。
一个程序执行的时候,CPU会根据PC寄存器里的地址,从内存里面把需要执行的指令读取到指令寄存器里面执行,然后根据指令长度自增,开始顺序读取下一条指令。一个程序的一条条指令,在内存里面是连续保存的,也会一条条顺序加载。而有些特殊指令,比如J类指令,也就是跳转指令,会修改PC寄存器里面的地址值。这样,下一条要执行的指令就不是从内存里面顺序加载的了。事实上,这些跳转指令的存在,也是在写程序的时候,可以使用if…else条件语句和while/for循环语句的原因。
4.为了理解J类指令的运行,用以下代码作为例子:
// test.c
#include
#include
int main()
{
srand(time(NULL));
int r = rand() % 2;
int a = 10;
if (r == 0)
{
a = 1;
} else {
a = 2;
}
}
用rand()生成了一个随机数r,要么是0,要么是1。当r是0时,变量a设成1,不然就设成2。将上面代码编译形成汇编代码后,if…else的部分如下:
if (r == 0)
3b: 83 7d fc 00 cmp DWORD PTR [rbp-0x4],0x0
3f: 75 09 jne 4a
{
a = 1;
41: c7 45 f8 01 00 00 00 mov DWORD PTR [rbp-0x8],0x1
48: eb 07 jmp 51
}
else
{
a = 2;
4a: c7 45 f8 02 00 00 00 mov DWORD PTR [rbp-0x8],0x2
51: b8 00 00 00 00 mov eax,0x0
}
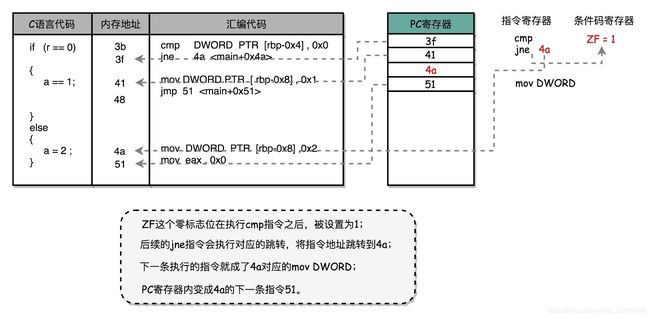
可以看到,这里对于r == 0的条件判断,被编译成了cmp和jne这两条指令。cmp 指令比较了前后两个操作数的值,这里的DWORD PTR代表操作的数据类型是32位的整数,而[rbp-0x4]则是一个寄存器的地址。所以,第一个操作数就是从寄存器里拿到的变量r的值。第二个操作数0x0就是设定的常量0的十六进制表示。cmp指令的比较结果,会存入到条件码寄存器当中去。这里如果比较的结果是True,也就是r == 0,就把零标志条件码(对应的条件码是ZF,Zero Flag)设置为1。除了零标志之外,Intel的CPU下还有进位标志(CF,Carry Flag)、符号标志(SF,Sign Flag)以及溢出标志(OF,Overflow Flag),用在不同的判断条件下。
cmp指令执行完成之后,PC寄存器会自动自增,开始执行下一条jne的指令。跟着的jne指令,是jump if not equal的意思,它会查看对应的零标志位。如果不为0,会跳转到后面跟着的操作数4a的位置。这个4a,对应汇编代码的行号,也就是上面设置的else条件里的第一条指令。当跳转发生的时候,PC寄存器就不再是自增变成下一条指令的地址,而是被直接设置成4a这个地址。这个时候,CPU再把4a地址里的指令加载到指令寄存器中来执行。
跳转到执行地址为4a的指令,实际是一条mov指令,第一个操作数和前面的cmp指令一样,是另一个32位整型的寄存器地址,以及对应的2的十六进制值0x2。mov指令把2设置到对应的寄存器里去,相当于一个赋值操作。然后,PC寄存器里的值继续自增,执行下一条mov指令。
这条mov指令的第一个操作数eax,代表累加寄存器,第二个操作数0x0则是十六进制的0的表示。这条指令其实没有实际的作用,它的作用是一个占位符。看前面的 if 条件,如果满足的话,在赋值的mov指令执行完成之后,有一个jmp的无条件跳转指令。跳转的地址就是这一行的地址51。main 函数没有设定返回值,而mov eax, 0x0其实就是给main函数生成了一个默认的为0的返回值到累加器里面。if条件里面的内容执行完成之后也会跳转到这里,和else里的内容结束之后的位置是一样的。
5.对于循环的实现,有如下的代码例子:
int main()
{
int a = 0;
for (int i = 0; i < 3; i++)
{
a += i;
}
}
对应的汇编代码如下:
for (int i = 0; i < 3; i++)
b: c7 45 f8 00 00 00 00 mov DWORD PTR [rbp-0x8],0x0
12: eb 0a jmp 1e
{
a += i;
14: 8b 45 f8 mov eax,DWORD PTR [rbp-0x8]
17: 01 45 fc add DWORD PTR [rbp-0x4],eax
for (int i = 0; i < 3; i++)
1a: 83 45 f8 01 add DWORD PTR [rbp-0x8],0x1
1e: 83 7d f8 02 cmp DWORD PTR [rbp-0x8],0x2
22: 7e f0 jle 14
24: b8 00 00 00 00 mov eax,0x0
}
可以看到,对应的循环也是用1e这个地址上的cmp比较指令,和紧接着的jle条件跳转指令来实现的。主要的差别在于,这里jle跳转的地址,在这条指令之前的地址14,而非if…else编译出来的跳转指令之后。往前跳转使得条件满足的时候,PC寄存器会把指令地址设置到之前执行过的指令位置,重新执行之前执行过的指令,直到条件不满足,顺序往下执行jle之后的指令,整个循环才结束。
其中jle和jmp指令,有点像程序语言里面的goto命令,直接指定了一个特定条件下的跳转位置。虽然在用高级语言开发程序的时候反对使用goto,但是实际在机器指令层面,无论是 if…else也好还是for/while,都是用和goto相同的跳转到特定指令位置的方式来实现的。因此,想要在硬件层面实现这个goto语句,除了需要用来保存下一条指令地址,以及当前正要执行指令的PC寄存器、指令寄存器外,只需要再增加一个条件码寄存器,来保留条件判断的状态。这样三个寄存器,就可以实现条件判断和循环重复执行代码的功能。
三、栈
6.可以通过以下代码例子解释,为什么程序要有“栈”这个概念:
#include
int static add(int a, int b)
{
return a+b;
}
int main()
{
int x = 5;
int y = 10;
int u = add(x, y);
}
将上述程序编译后,汇编代码如下所示:
int static add(int a, int b)
{
0: 55 push rbp
1: 48 89 e5 mov rbp,rsp
4: 89 7d fc mov DWORD PTR [rbp-0x4],edi
7: 89 75 f8 mov DWORD PTR [rbp-0x8],esi
return a+b;
a: 8b 55 fc mov edx,DWORD PTR [rbp-0x4]
d: 8b 45 f8 mov eax,DWORD PTR [rbp-0x8]
10: 01 d0 add eax,edx
}
12: 5d pop rbp
13: c3 ret
0000000000000014 :
int main()
{
14: 55 push rbp
15: 48 89 e5 mov rbp,rsp
18: 48 83 ec 10 sub rsp,0x10
int x = 5;
1c: c7 45 fc 05 00 00 00 mov DWORD PTR [rbp-0x4],0x5
int y = 10;
23: c7 45 f8 0a 00 00 00 mov DWORD PTR [rbp-0x8],0xa
int u = add(x, y);
2a: 8b 55 f8 mov edx,DWORD PTR [rbp-0x8]
2d: 8b 45 fc mov eax,DWORD PTR [rbp-0x4]
30: 89 d6 mov esi,edx
32: 89 c7 mov edi,eax
34: e8 c7 ff ff ff call 0
39: 89 45 f4 mov DWORD PTR [rbp-0xc],eax
3c: b8 00 00 00 00 mov eax,0x0
}
41: c9 leave
42: c3 ret
在这段代码里,main函数主要是把 jump指令换成了函数调用的call指令。call指令后面跟着的是跳转后的程序地址0。add函数编译之后,代码先执行了一条push指令和一条mov指令;在函数执行结束的时候,又执行了一条pop和一条ret指令。这四条指令的执行,其实就是在进行压栈(Push)和出栈(Pop)操作。
函数调用和if…else和for/while循环有点像。它们都是在原来顺序执行的指令过程里,执行了一个内存地址的跳转指令,让指令从原来顺序执行的过程里跳开,从新的跳转后的位置开始执行。 但是,这两个跳转有个区别,if…else 和for/while的跳转,是跳转走了就不再回来了,就在跳转后的新地址开始顺序地执行指令,而函数调用的跳转是在对应函数的指令执行完了之后,还要再回到函数调用的地方,继续执行call之后的指令。
那是否有一个可以不跳转回到函数定义的方法,实现函数的调用呢?直觉上似乎可以把调用的函数指令,直接插入在调用函数的地方,替换掉对应的 call 指令,然后在编译器编译代码的时候,直接就把函数调用变成对应的指令替换掉。但是这个方法有漏洞,如果函数A调用了函数B,然后函数B再调用函数A,就得面临在A里面插入B的指令,然后在B里面插入A的指令,这样就会产生无穷无尽地替换。就像两面镜子面对面放在一起,任何一面镜子里面都会看到无穷多面镜子。
因此,被调用函数的指令直接插入在调用处的方法行不通。那是否可以把后面要跳回来执行的指令地址给记录下来呢?就像PC寄存器一样,可以专门设立一个“程序调用寄存器”,来存储接下来要跳转回来执行的指令地址。等到函数调用结束,从这个寄存器里取出地址,再跳转到这个记录的地址,继续执行就好了。但是在多层函数调用里,简单只记录一个地址也是不够的。在调用函数A之后,A还可以调用函数B,B还能调用函数C。这一层层的调用是无限的。在所有函数调用返回之前,每一次调用的返回地址都要记录下来,但是CPU里的寄存器数量并不多,例如Intel i7只有16个64位寄存器,调用的层数一多就存不下了。
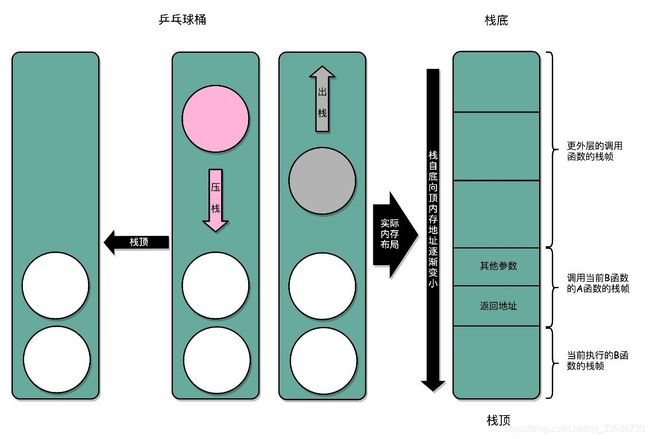
最终,科学家们想到了一个比单独记录跳转回来的地址更完善的办法,即在内存里面开辟一段空间,用栈这个后进先出(LIFO,Last In First Out)的数据结构。栈就像一个球桶,每次程序调用函数之前,我们都把调用返回后的地址写在一个球上,然后塞进这个球桶。这个操作其实就是压栈。如果函数执行完了,就从球桶里取出最上面的那个球,就是出栈。
拿到出栈的球,找到上面的地址,把程序跳转过去,就返回到了函数调用后的下一条指令了。如果函数A在执行完成之前又调用了函数B,在取出球之前,需要往球桶里塞一个球。而从球桶最上面拿球的时候,拿的也一定是最近一次的,也就是最下面一层的函数调用完成后的地址。球桶的底部,就是栈底,最上面的球所在的位置,就是栈顶,如下所示:
在真实的程序里,压栈的不只有函数调用完成后的返回地址。比如函数A在调用B时,需要传输一些参数数据,这些参数数据在寄存器不够用的时候也会被压入栈中。整个函数A所占用的所有内存空间,就是函数A的栈帧(Stack Frame)。而实际的程序栈布局,顶和底与球桶相比是倒过来的。栈底在最上面,栈顶在最下面,这样的布局是因为栈底的内存地址是在一开始就固定的。而一层层压栈之后,栈顶的内存地址是在逐渐变小而不是变大。
对应上面代码中add的汇编代码,main函数调用add函数时,add函数入口在 0~1 行,add函数结束之后在12~13行。调用第34行的call指令时,会把当前的PC寄存器里的下一条指令的地址压栈(例如函数A中执行到一半要调用B(),则将B()的栈帧压入栈顶,该栈帧中保存A()中本来B()调用完后要执行的下一个指令地址,PC寄存器中A()的下一条指令修改为B()的第一条指令),保留被调用函数结束后要执行的指令地址。
代码例子中add函数的第0行,push rbp这个指令就是在进行压栈。这里的rbp又叫栈帧指针(Frame Pointer),是一个存放了当前栈帧位置的寄存器。push rbp就把之前调用函数,也就是main函数的栈帧的栈底地址,压到栈顶。接着,第1行的命令mov rbp, rsp里,则是把rsp这个栈指针(Stack Pointer)的值复制到rbp里,而rsp始终会指向栈顶。这个命令意味着,rbp这个栈帧指针指向的地址,变成当前最新的栈顶,也就是add函数的栈帧的栈底地址了。
而在函数add执行完成之后,又会分别调用第12行的pop rbp来将当前的栈顶出栈,这部分操作维护好了整个栈帧。然后,可以调用第13行的ret指令,同时要把call调用的时候压入PC寄存器里的原函数下一条指令出栈,写回到PC寄存器中(调用跳转其他函数时,PC寄存器中存放的下一条要执行的指令被修改过,从原函数中下一条指令变成被调用函数的地址),将程序的控制权返回到出栈后的栈顶。
通过引入栈,可以看到无论有多少层的函数调用,或者在函数A里调用函数B,再在函数B里调用A这样的递归调用,都只需要通过维持rbp和rsp这两个维护栈顶所在地址的寄存器,就能管理好不同函数之间的跳转,相当于在指令跳转的过程中,加入了一个“记忆”的功能,能在跳转去运行新的指令之后,再回到跳出去的位置,实现更加丰富和灵活的指令执行流程。这样还提供了“函数”这样一个抽象,使得在软件开发的过程中,可以复用代码和指令,而不是只能简单粗暴地复制、粘贴代码。
但栈的大小也是有限的。如果函数调用层数太多(如太多层递归、栈内创建占内存的巨大数组变量等),往栈里压入它存不下的内容,程序在执行的过程中就会遇到栈溢出的错误,这就是“stack overflow”。
四、链接与内存装载
7. 函数调用需要维护栈与地址跳转,会产生一定开销,如果可以把被调用函数中的指令,直接插入到原函数中的位置,替换对应的函数调用指令,使指令按顺序地址执行下去,会提高性能。如果被调用的函数里,没有调用其他函数(这种函数叫叶子函数),这个方法是可行的。事实上,这就是一个常见的编译器进行自动优化的场景,叫函数内联(Inline),只要在 GCC 编译的时候,加上对应的一个让编译器自动优化的参数 -O,编译器就会在可行的情况下,进行这样的指令替换,代码例子如下所示:
#include
#include
#include
int static add(int a, int b)
{
return a+b;
}
int main()
{
srand(time(NULL));
int x = rand() % 5
int y = rand() % 10;
int u = add(x, y)
printf("u = %d\n", u)
}
编译出来的汇编代码,没有把add函数单独编译成之前例子那样的一段指令序列,而是在调用 u = add(x, y) 的时候,直接替换成了一个 add 指令,如下所示:
gcc -g -c -O function_example_inline.c
$ objdump -d -M intel -S function_example_inline.o
……
return a+b;
4c: 01 de add esi,ebx
除了依靠编译器的自动优化,还可以在定义函数的地方,加上inline关键字,来提示编译器对函数进行内联。内联带来的优化是,CPU需要执行的指令数变少了,根据地址跳转的过程不需要了,压栈和出栈的过程也不用了。不过内联并不是没有代价,内联意味着,把可以复用的程序指令在调用它的地方完全展开了。如果一个函数在很多地方都被调用了,那么就会展开很多次,整个程序占用的空间就会变大了。
8. C语言代码→编译为汇编代码→汇编成机器码的过程,计算机上进行的时候是由两部分组成的:
(1)第一部分由编译(Compile)、汇编(Assemble)以及链接(Link,将多个代码的目标文件与函数库连接起来,生成可执行文件,多个代码文件编译的目标文件不链接会无法执行)三个阶段组成。在这三个阶段完成之后,就生成了一个可执行文件。
(2)第二部分通过装载器(Loader)把可执行文件装载(Load)到内存中。CPU从内存中读取指令和数据,来开始真正执行程序。
如果将第6点中的例子代码中add()函数与main()函数分别放在2个文件里,分别编译成2个目标文件(Object File)后再链接成1个可执行文件(Executable Program),使用objdump命令会得到比第6点中长得多的反汇编结果,如下所示:
link_example: file format elf64-x86-64
Disassembly of section .init:
...
Disassembly of section .plt:
...
Disassembly of section .plt.got:
...
Disassembly of section .text:
...
6b0: 55 push rbp
6b1: 48 89 e5 mov rbp,rsp
6b4: 89 7d fc mov DWORD PTR [rbp-0x4],edi
6b7: 89 75 f8 mov DWORD PTR [rbp-0x8],esi
6ba: 8b 55 fc mov edx,DWORD PTR [rbp-0x4]
6bd: 8b 45 f8 mov eax,DWORD PTR [rbp-0x8]
6c0: 01 d0 add eax,edx
6c2: 5d pop rbp
6c3: c3 ret
00000000000006c4 :
6c4: 55 push rbp
6c5: 48 89 e5 mov rbp,rsp
6c8: 48 83 ec 10 sub rsp,0x10
6cc: c7 45 fc 0a 00 00 00 mov DWORD PTR [rbp-0x4],0xa
6d3: c7 45 f8 05 00 00 00 mov DWORD PTR [rbp-0x8],0x5
6da: 8b 55 f8 mov edx,DWORD PTR [rbp-0x8]
6dd: 8b 45 fc mov eax,DWORD PTR [rbp-0x4]
6e0: 89 d6 mov esi,edx
6e2: 89 c7 mov edi,eax
6e4: b8 00 00 00 00 mov eax,0x0
6e9: e8 c2 ff ff ff call 6b0
6ee: 89 45 f4 mov DWORD PTR [rbp-0xc],eax
6f1: 8b 45 f4 mov eax,DWORD PTR [rbp-0xc]
6f4: 89 c6 mov esi,eax
6f6: 48 8d 3d 97 00 00 00 lea rdi,[rip+0x97] # 794 <_IO_stdin_used+0x4>
6fd: b8 00 00 00 00 mov eax,0x0
702: e8 59 fe ff ff call 560
707: b8 00 00 00 00 mov eax,0x0
70c: c9 leave
70d: c3 ret
70e: 66 90 xchg ax,ax
...
Disassembly of section .fini:
...
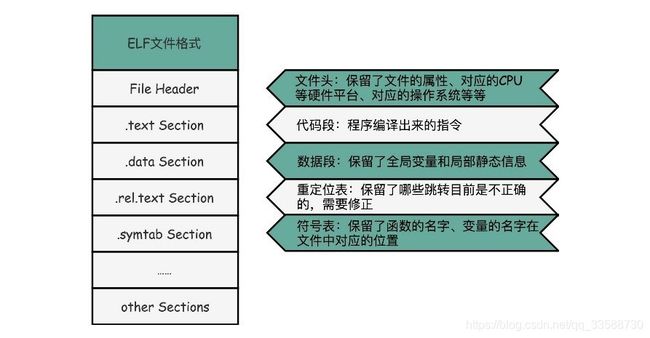
长了很多的原因是在Linux下,可执行文件和目标文件所使用的都是一种叫ELF(Execuatable and Linkable File Format)的文件格式,中文名叫可执行与可链接文件格式,这里面不仅存放了编译成的汇编指令,还保留了很多别的数据。 比如对应的函数名称如add、main等,乃至自定义的全局变量名称,都存放在这个ELF格式文件里。这些名字和它们对应的地址,在ELF文件里面,存储在一个叫作符号表(Symbols Table)的位置里。符号表相当于一个地址簿,把名字和地址关联了起来,如下所示:
链接器会扫描所有输入的目标文件,然后把各目标文件中符号表里的信息收集起来,构成一个全局的符号表。然后再根据重定位表,把所有不确定要跳转地址的代码,根据符号表里面存储的地址,进行一次修正。最后,把所有的目标文件的对应段进行一次合并,变成了最终的可执行代码。这样,可执行文件里面的函数调用地址都是正确的。
在链接器把程序变成可执行文件之后,要装载器去执行程序就容易多了。装载器不再需要考虑地址跳转的问题,只需要解析ELF文件,把对应的指令和数据,加载到内存里面供CPU执行就可以了。因此,同样一个程序在Linux 下可以执行而在Windows下不能执行了,其中一个重要原因就是两个操作系统下可执行文件的格式不一样。Linux 下是ELF文件格式,而Windows的可执行文件格式是PE(Portable Executable Format)。Linux下的Loader只能解析ELF格式而不能解析PE格式。
如果有一个可以能够解析PE格式的装载器,就有可能在Linux下运行Windows程序了,所以Linux下著名的开源项目Wine,就是通过兼容PE格式的装载器,使得能直接在Linux下运行Windows程序。而现在Windows也提供了WSL,也就是Windows Subsystem for Linux,可以解析和加载ELF格式的文件。
综上可知平时写的程序,也不仅仅是把所有代码放在一个文件里编译执行,而是可以拆分成不同的函数库,最后通过一个静态链接的机制,使得不同的文件之间既有分工,又能通过静态链接来“合作”,变成一个可执行的程序。对于ELF格式的文件,为了能够实现这样一个静态链接的机制,里面不只是简单罗列了程序所需要执行的指令,还会包括链接所需要的重定位表和符号表。
9. 链接器把多个目标文件合并成一个最终可执行文件,在运行这个可执行文件的时候,其实是通过一个装载器,解析ELF或者PE格式的可执行文件。Loader会把对应的指令和数据加载到内存里让CPU去执行,但具体并非直接加载进去那么简单,实际上装载器需要满足两个要求:
(1)可执行程序加载后占用的内存空间应该是连续的。执行指令的时候,程序计数器是顺序地一条一条指令执行下去。这也就意味着,这一条条指令需要连续地存储在一起。
(2)内存中需要同时加载很多个程序,并且不能让程序自己规定在内存中加载的位置。虽然编译出来的指令里已经有了对应的各种各样的内存地址,但是实际加载的时候,其实没有办法确保这个程序一定加载在哪一段内存地址上,因为计算机会同时运行很多个程序,想要的内存地址可能已经被其他加载的程序占用了。
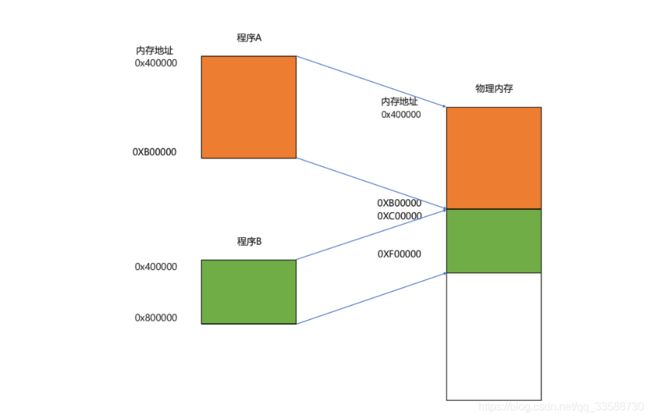
要满足这两个基本的要求,我们很容易想到一个办法。那就是可以在内存里面,找到一段连续的内存空间,然后分配给装载的程序,然后把这段连续的内存空间地址,和整个程序指令里指定的内存地址做一个映射。汇编指令里用到的内存地址叫作虚拟内存地址(Virtual Memory Address),实际在内存硬件里面的空间地址,叫物理内存地址(Physical Memory Address)。对于程序只需要关心虚拟内存地址就行了。所以只需要维护一个虚拟内存到物理内存的映射表,这样实际程序指令执行的时候,会通过虚拟内存地址,找到对应的物理内存地址,然后执行。因为是连续的内存地址空间,所以只需要维护映射关系的起始地址和对应的空间大小就可以了。
这种找出一段连续的物理内存和虚拟内存地址进行映射的方法叫分段(Segmentation)。这里的段,就是指系统分配出来的那个连续内存空间,如下所示:
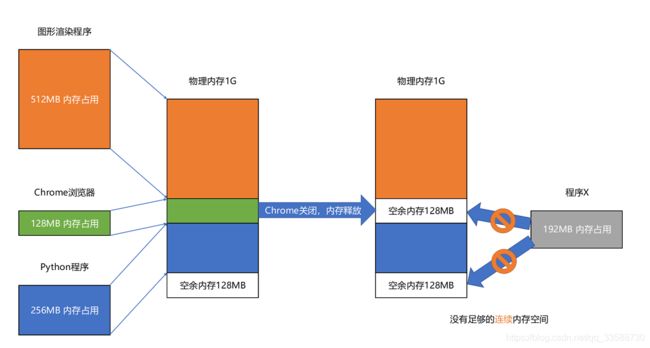
分段解决了程序本身不需要关心具体的物理内存地址的问题,但它也有不足之处,第一个就是内存碎片(Memory Fragmentation)问题。例如电脑有1GB内存,先启动一个图形渲染程序占用512MB的内存,接着启动一个Chrome占用了128MB内存,再启动一个Python程序占用256MB内存。此时关掉Chrome,于是空闲内存还有1024 - 512 - 256 = 256MB。按理来说有足够的空间再去装载一个200MB的程序,但是这256MB的内存空间不是连续的,而是被分成了两段128MB的内存。因此实际情况是该程序没办法加载进来。
解决的办法叫内存交换(Memory Swapping)。可以把Python程序占用的256MB内存写到硬盘上,然后再从硬盘上读回来到内存里面。不过读回来的时候,不再把它加载到原来的位置,而是紧紧跟在那已经被占用了的512MB内存后面。这样就有了连续的256MB内存空间,就可以去加载一个新的200MB的程序。安装Linux操作系统时会遇到分配一个swap硬盘分区的选项。这块分出来的磁盘空间,其实就是专门给Linux操作系统进行内存交换用的。
虚拟内存、分段,再加上内存交换,看起来似乎已经解决了计算机同时装载运行很多个程序的问题。不过这三者的组合仍然会遇到一个性能瓶颈。硬盘的访问速度要比内存慢很多,而每一次内存交换,都需要把一大段连续的内存数据写到硬盘上。所以,如果内存交换的时候,交换的是一个很占内存空间的程序,这样整个机器都会显得卡顿。
10.上述问题出在内存碎片和内存交换的空间太大上,那么解决问题的办法就是少出现一些内存碎片。另外,当需要进行内存交换的时候,让需要交换写入或者从磁盘装载的数据更少一点,就可以解决这个问题。这个办法,在计算机内存管理中叫作内存分页(Paging)。
和分段这样分配一整段连续空间给程序相比,分页是把整个物理内存空间切成一段段固定尺寸的大小。而对应的程序所需要占用的虚拟内存空间,也会同样切成一段段固定尺寸的大小。这样一个连续并且尺寸固定的内存空间叫页(Page)。从虚拟内存到物理内存的映射,不再是拿整段连续的内存的物理地址,而是按照一个一个页来。页的尺寸一般远远小于整个程序的大小。在 Linux 下通常为4KB,可以通过以下命令查看Linux系统设置的页大小:
getconf PAGE_SIZE由于内存空间都已预先划分为一个个page,也就没有了不能使用的一大段内存碎片。即使内存空间不够,需要让正在运行的其他程序通过内存交换释放出一些内存的页出来,一次性写入磁盘的也只有少数的一个页或者几个页,不会花太多时间让机器被内存交换过程给卡住。
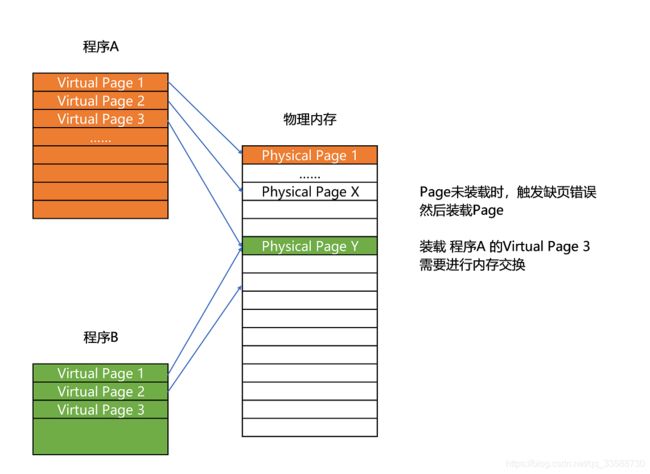
分页的方式使得在加载程序时,不再需要一次性把整个程序加载到物理内存中,完全可以在进行虚拟内存和物理内存页之间的映射之后,并不真的把页加载到物理内存里,而是只在程序运行中,需要用到对应虚拟内存页里面的指令和数据时,再加载到物理内存里面去。实际上操作系统的确是这么做的。当要读取特定的页,却发现数据并没有加载到物理内存里的时候,就会触发一个来自于CPU的缺页错误(Page Fault),操作系统会捕捉到这个错误,然后将对应的页从存放在硬盘上的虚拟内存里读取出来,加载到物理内存里。这种方式,使得可以运行那些远大于电脑实际物理内存的程序。
同时,这样任何程序都不需要一次性加载完所有指令和数据,只需要加载当前需要用到就行了。通过虚拟内存、内存交换和内存分页这三个技术的组合,最终得到了一个让程序不需要考虑实际的物理内存地址、大小和当前分配空间的解决方案。这些技术和方法,对于程序的编写、编译和链接过程都是透明的。通过引入虚拟内存、页映射和内存交换,程序本身就不再需要考虑对应的真实内存地址、程序加载、内存管理等问题了。任何一个程序,都只需要把内存当成是一块完整而连续的空间来直接使用。
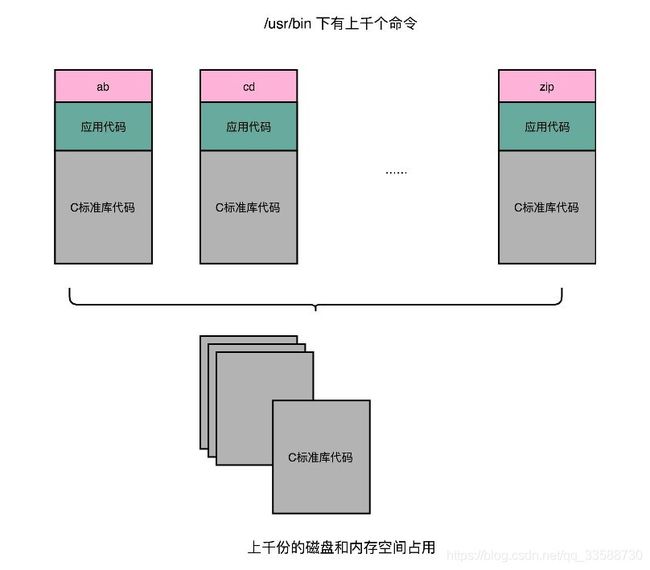
11.程序的链接,是把对应不同文件内的代码段合并到一起,成为最后的可执行文件。这个链接的方式,在写代码的时候做到了“复用”。同样的功能代码只要写一次,然后提供给很多不同的程序进行链接就行了。但是,如果有很多个程序都要通过装载器装载到内存里面,那各程序链接好的相同功能代码,也都需要再装载一遍,再占一遍内存空间,造成浪费,如下所示:
如果能够让同样功能的代码,在与不同的N个程序链接时,不需要占N份内存空间,就能减少内存空间浪费,这个思路就引入一种新的链接方法,叫作动态链接(Dynamic Link)。相应的之前的合并多份代码段的方法,就是静态链接(Static Link)。在动态链接的过程中,想要“链接”的不是存储在硬盘上的目标文件代码,而是加载到内存中的共享库(Shared Libraries)。
这个加载到内存中的共享库会被很多个程序的指令调用到。在Windows下,共享库文件就是.dll文件,也就是 Dynamic-Link Libary(DLL,动态链接库)。在Linux下,共享库文件就是.so文件,也就是Shared Object(也称之为动态链接库)。这两大操作系统下的文件名后缀,一个用了“动态链接”的意思,另一个用了“共享”的意思,表明了这样的思路。
要想要在程序运行的时候共享代码,也有一定的要求,就是这些机器码必须是“地址无关”的。也就是说,编译出来的共享库文件的指令代码,是地址无关码(Position-Independent Code)。也就是这段代码,无论加载在哪个内存地址,都能够动态链接自己写的程序并正常执行(如加法和打印)。如果不是这样的代码,就是地址相关的代码(如绝对地址代码、利用重定位表的代码)。其中重定位表在程序链接的时候,就把函数调用后要跳转访问的地址确定下来了,这意味着,如果这个函数加载到一个不同的内存地址,跳转就会失败。
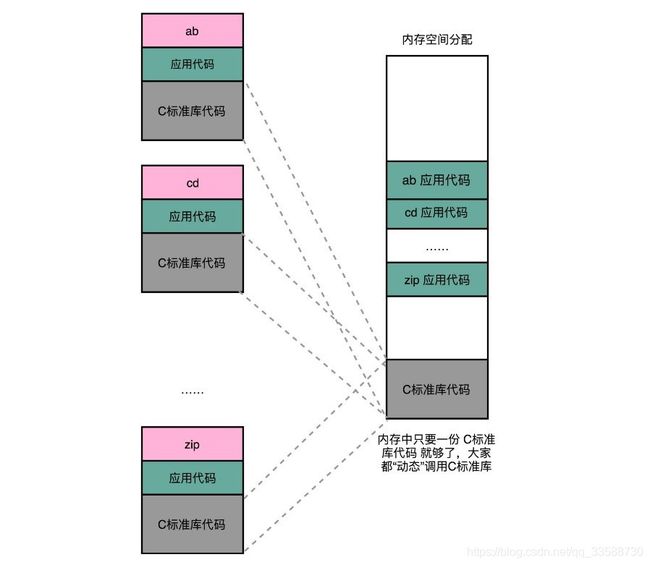
对于所有动态链接共享库的程序来讲,虽然共享库用的都是同一段物理内存地址,但是在不同的应用程序里,它所在的虚拟内存地址是不同的,如下所示:
动态代码库内部的变量和函数调用只需要使用相对地址(Relative Address)就可以保证地址无关。各种指令中使用到的内存地址,给出的不是一个绝对的地址空间,而是一个相对于当前指令偏移量的内存地址。因为整个共享库是放在一段连续的虚拟内存地址中的,无论装载到哪一段地址,不同指令之间的相对地址都是不变的。
12.以下的代码例子实现了动态链接共享库,首先是头文件:
// lib.h
#ifndef LIB_H
#define LIB_H
void show_me_the_money(int money);
#endif
下面的lib.c包含了头文件的实际实现:
// lib.c
#include
void show_me_the_money(int money)
{
printf("Show me USD %d from lib.c \n", money);
}
最后一个包含main函数的文件调用了lib.h里的函数:
// show_me_poor.c
#include "lib.h"
int main()
{
int money = 5;
show_me_the_money(money);
}
最后在Linux系统上将show_me_poor.c编译为一个动态链接库,即.so文件,可以看到,在编译的过程中指定了一个-fPIC的参数。这个参数其实就是Position Independent Code的意思,也就是要把这个编译成一个地址无关代码。然后,再通过gcc编译show_me_poor动态链接了lib.so的可执行文件:
gcc lib.c -fPIC -shared -o lib.so
$ gcc -o show_me_poor show_me_poor.c ./lib.so
在这些操作都完成了之后,把show_me_poor这个文件通过objdump反编译出来看一下:
objdump -d -M intel -S show_me_poor
……
0000000000400540 :
400540: ff 35 12 05 20 00 push QWORD PTR [rip+0x200512] # 600a58 <_GLOBAL_OFFSET_TABLE_+0x8>
400546: ff 25 14 05 20 00 jmp QWORD PTR [rip+0x200514] # 600a60 <_GLOBAL_OFFSET_TABLE_+0x10>
40054c: 0f 1f 40 00 nop DWORD PTR [rax+0x0]
0000000000400550 :
400550: ff 25 12 05 20 00 jmp QWORD PTR [rip+0x200512] # 600a68 <_GLOBAL_OFFSET_TABLE_+0x18>
400556: 68 00 00 00 00 push 0x0
40055b: e9 e0 ff ff ff jmp 400540 <_init+0x28>
……
0000000000400676 :
400676: 55 push rbp
400677: 48 89 e5 mov rbp,rsp
40067a: 48 83 ec 10 sub rsp,0x10
40067e: c7 45 fc 05 00 00 00 mov DWORD PTR [rbp-0x4],0x5
400685: 8b 45 fc mov eax,DWORD PTR [rbp-0x4]
400688: 89 c7 mov edi,eax
40068a: e8 c1 fe ff ff call 400550
40068f: c9 leave
400690: c3 ret
400691: 66 2e 0f 1f 84 00 00 nop WORD PTR cs:[rax+rax*1+0x0]
400698: 00 00 00
40069b: 0f 1f 44 00 00 nop DWORD PTR [rax+rax*1+0x0]
……
可以看到,main()调用show_me_the_money()时,对应汇编代码为call 400550
在动态链接对应的共享库中,data section里面,保存了一张全局偏移表(GOT,Global Offset Table)。虽然共享库的代码部分的物理内存是共享的,但是数据部分是各个动态链接它的程序里面各加载一份的。所有需要引用当前共享库外部地址的指令,都会查询GOT,来找到当前运行程序的虚拟内存里的对应位置。
而GOT表里的数据,则是在加载一个个共享库的时候写进去的。不同的进程,调用同样的lib.so,各自GOT里面指向最终加载的动态链接库里面的虚拟内存地址是不同的。 这样,虽然不同的程序调用的同样的动态库,各自的内存地址是独立的,也不需要去修改动态库里面的代码所使用的地址,而是各个程序各自维护好自己的GOT,能够找到对应的动态库就好了,如下所示:
GOT表位于共享库自己的data section里。GOT表在内存里和对应的代码段位置之间的偏移量,始终是确定的。这样,共享库就是地址无关的代码,对应的各个程序只需要在物理内存里面加载这同一份代码。同时,也要通过各可执行文件在load进内存时,生成的各不相同的GOT表,来找到该程序需要调用到的共享库外部变量和函数的地址。这是一个典型的不修改代码,而是通过修改“地址数据”来进行关联的办法,有点像C语言里面用函数指针来调用对应的函数,并不是通过预先已经确定好的函数名称来调用,而是利用当时它在内存里面的动态地址来调用。
在进行Linux下的程序开发时,一直会用到各种各样的动态链接库。C语言的标准库就在1MB以上,撰写任何一个程序可能都需要用到这个库,常见的Linux服务器里,/usr/bin下有上千个可执行文件,如果每一个都把标准库静态链接进程序,几GB乃至几十GB的磁盘空间一下子就用掉了。如果服务端的多进程应用要开上千个进程,几GB 的内存空间也会一下子就用掉了。动态链接解决了静态链接浪费虚拟与物理内存空间的问题。
五、二进制编码
13. 程序 = 算法 + 数据结构。如果对应到组成原理或者说硬件层面,算法就是各种计算机指令,数据结构就对应二进制数据。在早期,字符串(Character String)只需要使用英文字符,加上数字和一些特殊符号,然后用8位的二进制,就能表示日常需要的所有字符了,这就是常说ASCII码(American Standard Code for Information Interchange,美国信息交换标准代码)。
ASCII码好比一个字典,用8位二进制中的128个不同的数,映射到128个不同的字符里。比如,a在ASCII里就是第97个,也就是二进制的0110 0001,对应的十六进制表示就是61。而A就是第65个,也就是二进制的0100 0001,对应的十六进制表示就是41。在ASCII码里数字9不再像整数表示法里一样,用0000 1001来表示,而是用0011 1001来表示。字符串15也不是用0000 1111这8位来表示,而是变成两个字符1和5连续放在一起,也就是0011 0001和0011 0101,需要用两个8位来表示。
因此,最大的32位整数即2147483647,如果用整数表示法,只需要32位就能表示了。但是如果用字符串来表示,一共有10个字符,每个字符用8位的话,需要整整80位。比起整数表示法,要多占很多空间。这也是为什么,很多时候在存储数据的时候,要采用二进制序列化方式,而不是简单地把数据通过CSV或者JSON这样的文本格式存储来进行序列化。不管是整数也好,浮点数也好,采用二进制序列化会比存储文本省下不少空间。
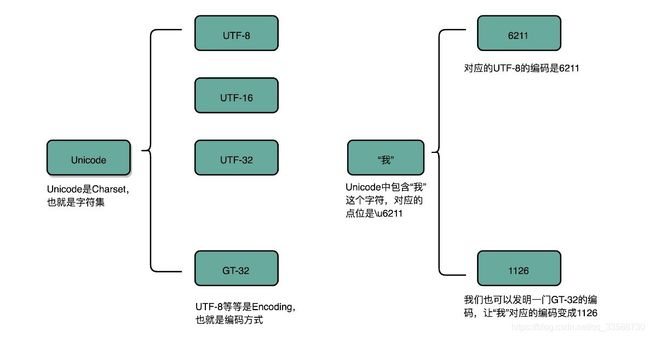
ASCII码只表示了128个字符,早期还算够用,然而随着越来越多的不同国家的人都用上了计算机,想要表示中文这样的文字,128个字符是不够的。于是,计算机工程师们给自己国家的语言创建了对应的字符集(Charset)和字符编码(Character Encoding)。字符集表示的是字符的一个集合,比如“中文”就是一个字符集,再比如 Unicode其实就是一个字符集,包含了150种语言的14万个不同字符。字符编码则是对于字符集里的这些字符,如何用二进制表示出来的一个字典。Unicode就可以用UTF-8、UTF-16,乃至UTF-32来进行编码,存储成二进制,如下所示:
同样的文本,采用不同的编码存储下来。如果另一个程序用一种不同的编码方式来进行解码和展示,就会出现乱码。这就好比用GB2312,去解密别人用 UTF-8 加密的信息,自然无法读出有用的信息。
六、加减法
14.计算机只有加法器,没有减法器,因为当初减法器的硬件实现性能开销较大,最终选择了用加法器来作减法。正数相加与负数单独相加可以用原码表示,但是正数与负数相加时原码的表示就有问题了。例如,对于负数来说,可以把一个数最左侧的一位,当成是对应的正负号,0为正数,1为负数。这样,一个4位的二进制数,0011就表示为+3。而1011最左侧的第一位是1,假如它表示-3,那这样的原码表示法有一个很直观的缺点:0可以用两个不同的编码来表示,即1000代表-0,0000代表+0,这样就不能完全做到二进制和十进制的一一对应,而且还会出现0001 + 1001 = 1010即1+(-1)= -2等相反数相加不为0的错误情况。
为了解决这种错误情况,就出现了反码。正数的反码依然是本身原码,而负数例如-3的原码是1011,符号位保持不变,低三位011按位取反得100,所以-3的反码为1100。反码解决了原码的相反数相加时不为0的情况,如0001 + 1110 = 1111即1+(-1)= -0,但是反码会出现两个负数相加结果不正确的问题,例如1110 + 1100 = 1010即-1 + (-3) = -5。
因此,为了解决上述两个问题,出现了补码。大部分书上负数补码的定义都是其正数的原码所有位取反变为反码再加1,但其实算补码之前不一定必须先求正数的反码,负数的补码也等于它的原码自低位向高位,尾部的第一个‘1’及其右边的‘0’保持不变,左边的各位按位取反,符号位不变为1。所以,负数补码只是正好等于正数反码加1而已,并非定义上计算就是这样的。
在补码中,依然通过最左侧第一位的0和1来判断数的正负,但是不再把这一位当成独立的符号位不加入运算中,而是在计算整个二进制值的时候,在最左侧的符号位也加入运算。比如一个4位的二进制补码数值1011转换成十进制,就是−1×2^3+0×2^2+1×2^1+1×2^0 = −5。如果左侧最高位是1,这个数必然是负数;最高位是0,必然是正数。并且,只有0000表示0,1000在这样的情况下表示-8。一个4位的二进制数,可以表示从-8到7这16个整数,不会白白浪费一位。更重要的一点是,用补码来表示负数,使得整数相加变得很容易,不需要做任何电路改造等特殊处理,只是把它当成普通的二进制相加,就能得到正确的结果。因此反码、补码的产生过程,就是为了解决计算机做减法和引入符号位(正号和负号)的问题。
那么为什么使用补码和加法器,就能做减法呢?这就像是时钟,10点钟减2小时为8点钟,但是10点钟加上10小时也为8点钟(下午),只不过时针多走了一轮(就像产生进位),减数2和加数10加起来正好是钟上的12小时,那么2和10在时钟这个场景互为同余数,12为模。其实减去一个数,对于数值有限制,有溢出的运算(模运算)来说,也相当于加上这个减数的同余数。例如希望0110减去0010即6 – 2 = 4,只有加法器可以用,而4位二进制数的模即最大容量为16,表示为10000(溢出了1位),那么减数2的同余数,在这里就是10000-0010=1110即14。因此这两种计算等同:
0110(6)- 0010(2)= 0110(6)+ 1110(14) = 10100(20=16+4)
因为是4位二进制数,所以最高位的1溢出,剩下0100就是4了!6+14在这里等同于6-2,因为14的二进制1110就是-2补码的二进制表示。补码运算的原理借鉴了生活中的模运算。
七、门电路、加法器、乘法器
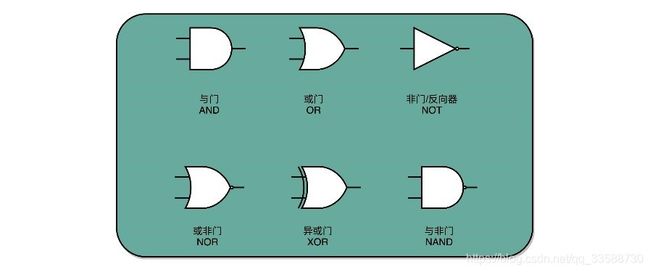
15.CPU中的各种逻辑功能,其实就靠下面这几种逻辑门组成:
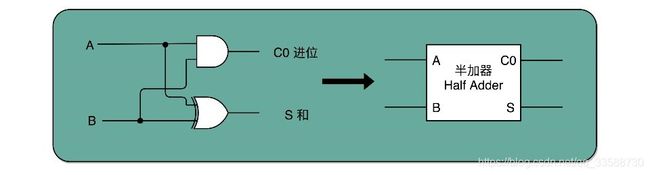
其中异或门就是一个最简单的整数加法,所需要使用的基本门电路,因为在二进制加法中,需要计算的两位是00和11的情况下,加法结果都应该是0;在输入的两位是10和01的情况下,输出都是1。当相加的两位都是1时,还需要向更左侧的一位进行进位。这就对应一个与门。所以,通过一个异或门计算出个位,通过一个与门计算出是否进位,就通过电路算出了一个一位数的加法。于是,把两个门电路结合,就变成半加器(Half Adder),如下所示:
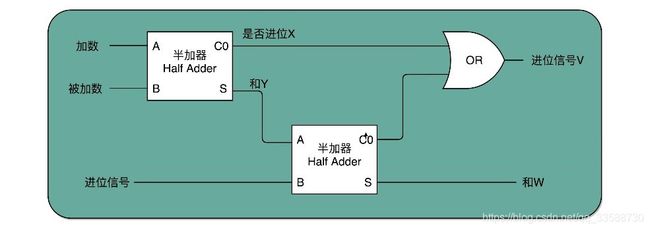
半加器可以解决最低位上的加法问题,但是如果左侧有第二位就不够用了。平常十进制竖式加法结果从右到左位个位、十位和百位等,二进制运算如果写成竖式,右往左数第二列就是“二位”,对应的再往左就分别是四位、八位。 在二位除了一个加数和被加数之外,还需要加上来自最低位的进位信号,一共需要三个数进行相加,才能得到结果。但是半加器输入都只能是两个bit,也就是两个电路通断开关,因此多位加法只用半加器还不够。为了进行多位加法,可以用两个半加器和一个或门,组合成一个全加器,如下所示:
第一个半加器用于最低位加法,得到是否进位X和最低位二个数相加后的结果Y这2个输出。然后,把最低位相加后的结果Y,和最低位相加后输出的进位信息U,再连接到一个半加器上,就会得到一个是否进位的信号V和第二位相加后的结果W。这个W就是在第二位上留下的结果。把两个半加器的进位输出,作为一个或门的输入连接起来,只要两次加法中任何一次需要进位,那么在二位上,就会向左侧的四位进一位。因为一共只有三个bit相加,即使3个bit都是1,也最多会进一位。
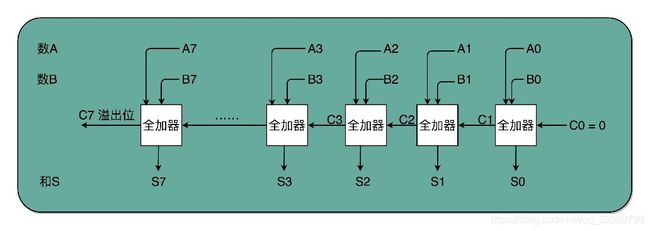
有了全加器,要进行对应的两个8 bit数的加法就很容易了,只要把8个全加器串联起来就好了。个位全加器的进位信号作为二位全加器的输入信号,二位全加器的进位信号再作为四位全加器的进位信号,这样一层层串接八层,就得到了一个支持8位数加法的算术单元,如下所示:
唯一需要注意的是,这样的全加器在最低位只需要用一个半加器,或者让全加器的进位输入始终是0,因为最低位没有来自更右侧的进位。而最左侧的一位输出的进位信号,表示的并不是再进一位,而是表示加法是否溢出了。因此,在整个加法器的结果中,其实有一个电路的信号,会标识出加法的结果是否溢出。可以把这个对应的信号输出到硬件中其他标志位里,让计算机知道计算的结果是否溢出。这就是为什么在撰写程序的时候,能够知道计算结果是否溢出在硬件层面得到的支持。
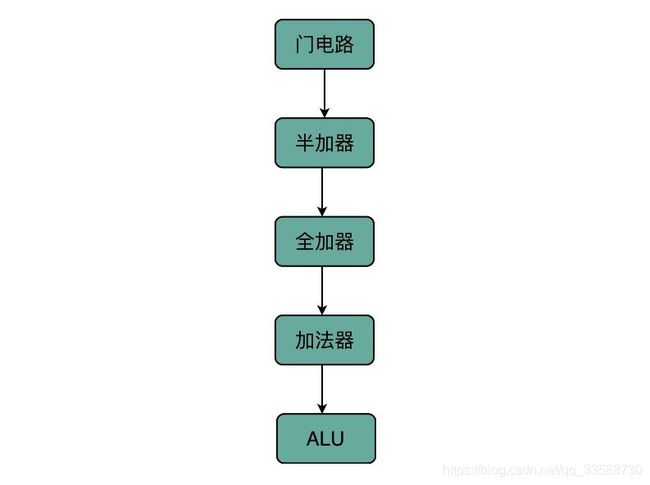
16.上面的门电路组成了半加器,半加器组成了全加器,全加器最终组成了加法器以及算术逻辑单元ALU,这其实就是计算机中,无论软件还是硬件中一个很重要的设计思想,分层。
从简单到复杂,这样一层层搭出了拥有更强能力的功能组件。在下面的一层,只需要考虑怎么用上一层的组件搭建出自己的功能,而不需要考虑跨层的其他组件。就像之前并没有深入学习过计算机组成原理,一样可以直接通过高级语言撰写代码,实现功能。当进一步打造强大的 CPU 时,就不会再去关注最细颗粒的门电路,只需要把门电路组合而成的ALU,当成一个能够完成基础计算的黑盒就可以了。
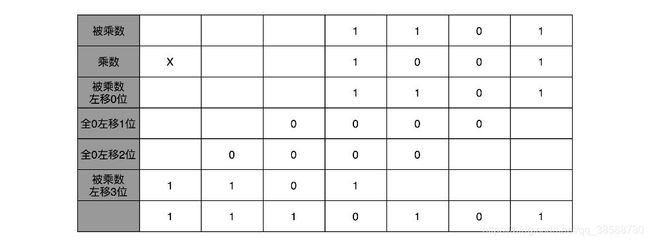
17.在计算机的乘法实现中,例如十进制中13乘以9,计算的结果是117,通过转换成二进制,然后列竖式的办法,在计算机看来整个计算过程实际上如下:
二进制的乘法有个很大的优点,就是这个过程与九九乘法口诀表无关。因为单个位置上,乘数只能是0或者1,所以实际的乘法就退化成了位移和加法。在13×9这个例子里,被乘数13的二进制是1101,乘数9的二进制是1001。1001最右边的个位是1,所以个位乘以被乘数1101,就是把1101复制下来。因为1001的二位和四位都是0,所以乘以被乘数都是0,那么保留下来的都是0000。乘数9的八位是1,所以仍然需要把被乘数1101复制下来。不过这里和个位位置的单纯复制有一点差别,那就是要把复制的1101向左侧移三位,最后把四位单独进行乘法与位移的结果进行求和,就得到了最终结果。
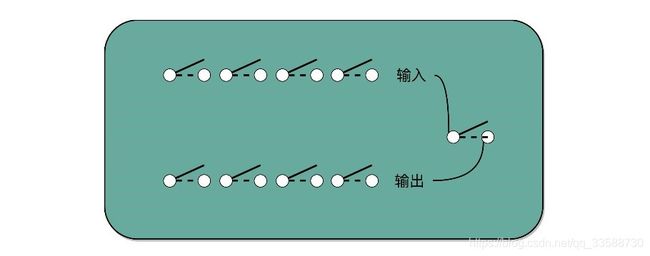
对应到数字电路和 ALU,可以看到最后一步的加法,可以用加法器来实现。乘法因为只有“0”和“1”两种情况,所以可以做成输入输出都是4个开关,中间用1个开关,同时来控制8个开关的方式,这就实现了二进制下的单位的乘法,如下所示:
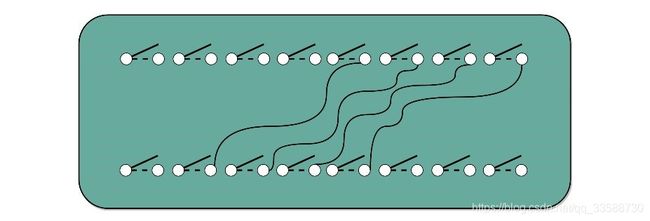
至于被乘数遇到乘数的1时进行位移,只要斜着错开位置去接线就好了。如果要左移一位,就错开一位接线;如果要左移两位,就错开两位接线,如下所示:
这样并不需要引入任何新的、更复杂的电路,仍然用最基础的电路,只要用不同的接线方式,就能够实现一个“列竖式”的乘法。而且,因为二进制下,只有0和1,也就是开关的开和闭这两种情况,所以计算机也不需要去“背诵”九九乘法口诀表,不需要单独实现一个更复杂的电路,就能够实现乘法。
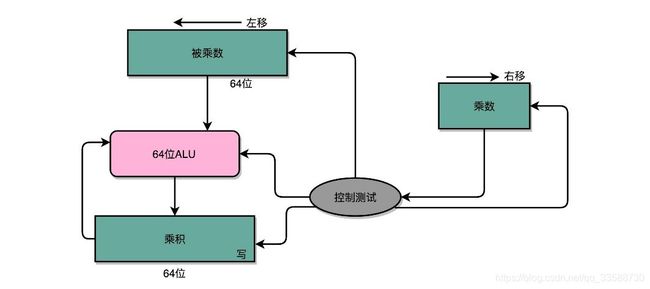
为了节约一点开关,也就是晶体管的数量,实际上像13×9这样两个四位二进制数的乘法,不需要把四次单位乘法的结果,用四组独立的开关单独都记录下来,然后再把这四个数加起来,因为这样做,需要很多组开关,太浪费晶体管了。如果顺序地来计算,只需要一组开关就好了。先拿乘数最右侧的个位乘以被乘数,然后把结果写入用来存放计算结果的开关里面,然后,把被乘数左移一位,把乘数右移一位,仍然用乘数去乘以被乘数,然后把结果加到刚才的结果上。反复重复这一步骤,直到不能再左移和右移位置。这样,乘数和被乘数就像两列相向而驶的列车,仅仅需要简单的加法器、一个可以左移一位的电路和一个右移一位的电路,就能完成整个乘法,如下所示:
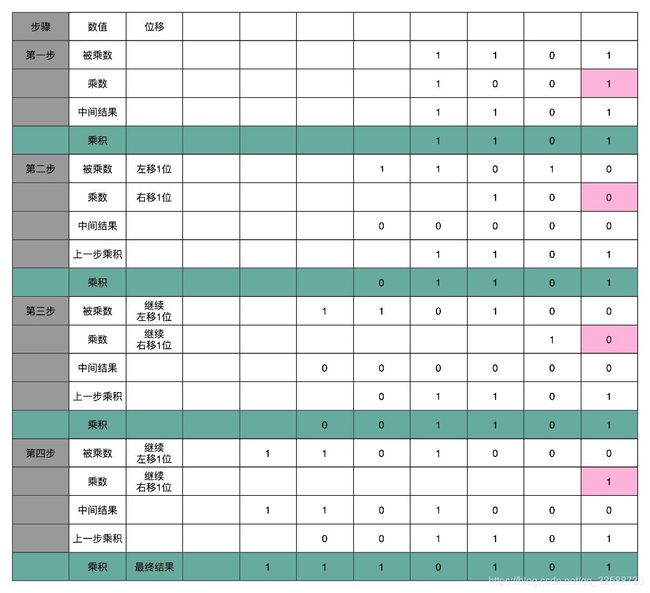
这里的控制测试,其实就是通过一个时钟信号,来控制左移、右移以及重新计算乘法和加法的时机。还是以计算13×9,也就是二进制的1101×1001的例子来看,如下所示:
这个计算方式虽然节约电路,但是计算速度慢。在这个乘法器的实现过程里,其实就是把乘法展开,变成了“加法+位移”来实现。用的是4位数,所以要进行4组“位移+加法”的操作,而且这4组操作还不能同时进行,因为下一组的加法要依赖上一组的加法后的计算结果,下一组的位移也要依赖上一组的位移的结果。这样,整个算法是“顺序”的,每一组加法或者位移的运算都需要一定的时间。
所以,最终这个乘法的计算速度,其实和要计算的数的位数有关。比如,这里的4位,就需要4次加法。而现代CPU常常要用32位或者是64位来表示整数,那么对应就需要32次或者64次加法。比起4位数,要多花上8倍乃至16倍的时间。在算法和数据结构中的术语中,这样的一个顺序乘法器硬件进行计算的时间复杂度是O(N)。这里的N就是乘法的数里面的位数。
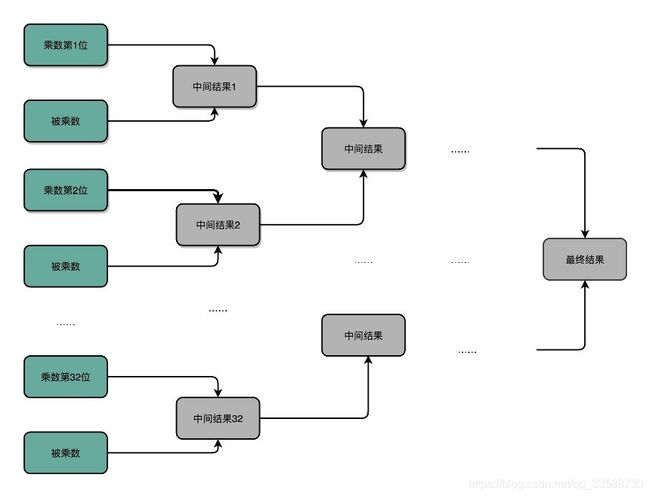
18.为了把上述乘法的时间复杂度降下来,在涉及CPU和电路的时候,可以改电路。32位数虽然是32次加法,但是可以让很多加法同时进行。把位移和乘法的计算结果加到中间结果里的方法,32位整数的乘法其实就变成了32个整数相加。前面顺序乘法器硬件的实现办法,就好像守擂赛,只有一个擂台会存下最新的计算结果。每一场新的比赛就来一个新的选手,实现一次加法,实现完了剩下的还是原来那个守擂的,直到其余31个选手都上来比过一场,一共要比31场。
加速的办法,就是把比赛变成像世界杯那样的淘汰赛,32个球队两两同时开赛。这样一轮一下子就淘汰了16支队,也就是说,32个数两两相加后,可以得到16个结果。后面的比赛也是一样同时两两开赛。只需要5轮也就是O(log2N)的时间就能得到计算的结果。但是这种方式要求我们得有16个球场。因为在淘汰赛的第一轮,需要16场比赛同时进行,对应到CPU的硬件上,就是需要更多的晶体管开关,来放下中间计算结果,如下所示:
之所以不经优化的加法与乘法计算会慢,核心原因其实是“顺序”计算,也就是说要等前面的计算结果完成之后,才能得到后面的计算结果。最典型的例子就是加法器,每一个全加器,都要等待上一个全加器,把对应的进入输入结果算出来,才能算下一位的输出。位数越多,越往高位走,等待前面的步骤就越多,这个等待的时间叫作门延迟(Gate Delay)。每通过一个门电路,就要等待门电路的计算结果,就是一层的门电路延迟,一般给它取一个“T”作为符号。一个全加器,其实就已经有了3T的延迟(进位需要经过 3 个门电路)。而4位整数,最高位的计算需要等待前面三个全加器的进位结果,也就是要等9T的延迟。如果是64位整数,就要变成63×3=189T的延迟。
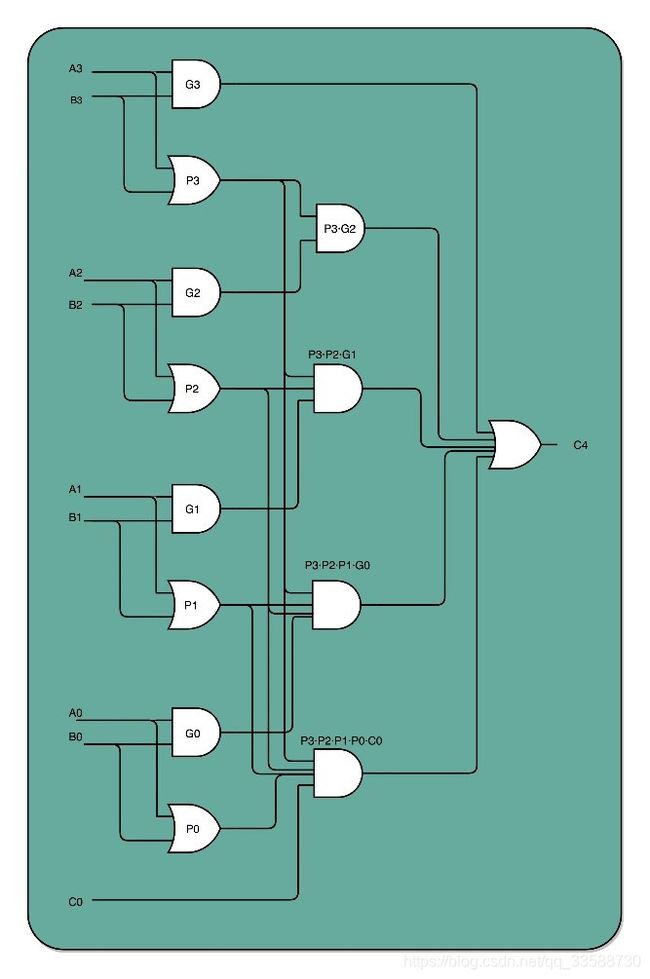
除了门延迟之外,还有一个问题就是时钟频率。在上面的顺序乘法计算里面,如果想要用更少的电路,计算的中间结果需要保存在寄存器里面,然后等待下一个时钟周期的到来,控制测试信号才能进行下一次移位和加法,这个延迟比上面的门延迟更大。解决这个问题就是在进行加法的时候,如果相加的两个数是确定的,那高位是否会进位其实也是确定的。可以把电路连结得复杂一点,让高位不需要等待低位的进位结果,而是把低位的所有输入信号都放进来,直接计算出高位的计算结果和进位结果。只要把进位部分的电路完全展开就好了,门电路的计算逻辑,可以像数学里的多项式乘法一样完全展开。在展开之后,可以把原来需要数量较少的,但是有较多层前后计算依赖关系的门电路,展开成数量较多的,但是依赖关系更少的门电路,如下所示,其中C4是前4位的计算结果是否进位的门电路表示,整个电路由与门(左侧平,用于进位)和异或门(左侧凹陷,用于求和)结合的多个半加器组成:
一个4位整数最高位是否进位,展开门电路后,只需要3T的延迟就可以拿到是否进位的计算结果。而对于64位的整数,也不会增加门延迟,只是从上往下复制这个电路,接入更多的信号而已。通过把电路变复杂,就解决了延迟的问题。这个优化,本质上是利用了电路天然的并行性。无论是这里把对应的门电路逻辑进行完全展开以减少门延迟,还是上面的乘法通过并行计算多个位的乘法,都是把完成一个计算的电路变复杂了,也就意味着晶体管变多了,所以晶体管的数量增加可以优化计算机的计算性能。实际上,这里的门电路展开和上面的并行计算乘法都是很好的例子,通过更多的晶体管,就可以拿到更低的门延迟,以及用更少的时钟周期完成一个计算指令。
通过ALU和门电路,搭建出来了乘法器,很多在生活中不得不顺序执行的事情,通过简单地连结一下线路,就变成并行执行了。通过精巧地设计电路,用较少的门电路和寄存器,就能够计算完成乘法这样相对复杂的运算。是用更少更简单的电路,但是需要更长的门延迟和时钟周期;还是用更复杂的电路,但是更短的门延迟和时钟周期来计算一个复杂的指令,这之间的权衡,其实就是计算机体系结构中RISC和CISC的经典历史路线之争。
八、不精确的浮点数
19.浮点数float的计算结果是不准确的。例如在Python中,0.3+0.6并不等于0.9,如下所示:
>>> 0.3 + 0.6
0.8999999999999999
计算机通常用16/32个比特(bit)来表示一个数,用32个比特,不能表示所有实数,只能表示2的32次方个不同的数,差不多是40亿个。如果表示的数要超过这个数,就会有两个不同的数的二进制表示是一样的。那计算机就会不知道这个数到底是多少,这个时候,计算机的设计者们就会面临一个问题:应该让这40亿个数映射到实数集合上的哪些数,在实际应用中才最划得来。
如果用4个比特来表示0~9的整数,那么32个比特就可以表示8个这样的整数。然后把最右边的2个0~9的整数当成小数部分;把左边6个0~9的整数当成整数部分。这样就可以用32个比特,来表示从0到999999.99这样1亿个实数了。这种用二进制来表示十进制的编码方式,叫作BCD编码(Binary-Coded Decimal)。它的运用非常广泛,最常用的是在超市、银行这样需要用小数记录金额的情况里。
这样的表示方式也有几个缺点。第一,这样的表示方式有点“浪费”。本来32个比特可以表示40亿个不同的数,但是在BCD编码下只能表示1亿个数,如果要精确到分的话,那么能够表示的最大金额也就是到100万。第二,这样的表示方式没办法同时表示很大的数字和很小的数字。在写程序的时候,实数的用途可能是多种多样的。有时候想要表示商品的金额,关心的是9.99这样小的数字;有时候又要进行物理学的运算,需要表示光速这样很大的数字。这时就需要一个办法,既能够表示很小的数又能表示很大的数,同时不会超过32或64位存储位数。
此时浮点数(Floating Point)即float类型应运而生。IEEE的标准定义了两个基本的格式,一个是用32比特表示单精度的浮点数,也就是常说的float或者float32类型,另外一个是用64比特表示双精度的浮点数,也就是平时说的double或者float64类型。单精度float类型的结构如下所示:
单精度的32个比特可以分成三部分:
(1)一个符号位,用来表示是正数还是负数。一般用s来表示。在浮点数里,所有的浮点数都是有符号的。
(2)一个8个比特组成的指数位,一般用e来表示。8个比特能够表示的整数空间,就是0~255,在这里用1~254映射到-126~127这254个有正有负的数上,这里没有用到0和255,没错,这里的0(也就是8个比特全部为0) 和255(也就是8个比特全部为1)另有它用,下面会讲到。
(3)一个23个比特组成的有效数位,用f来表示。综合科学计数法,浮点数就可以表示成下面这样:
(−1)^s × 1.f × 2^e
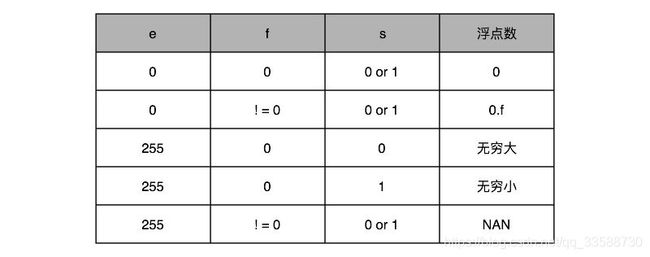
显然,这里的浮点数没有办法直接表示0。要表示0和一些特殊的数,就要用上在e里面留下的0和255这两个标识,其实是两个标记位。在e为0且f为0的时候,就把这个浮点数认为是0。至于其它的e是0或者255的特殊情况,可以看下面这个表格,分别可以表示出无穷大、无穷小、NAN 以及一个特殊的不规范数:
以0.5为例子,s应该是0,f应该是0,而e应该是-1,即0.5 = (−1)^0 × 1.0×2^(−1) = 0.5,对应的浮点数表示,就是 32个比特,如下所示:
需要注意,e表示从-126到127,-1是其中的第126个数,因此e用整数表示,就是 2^6+2^5+2^4+2^3+2^2+2^1=126,对应二进制就是01111110,而1.f=1.0所以f为0。
在这样的表示方式下,浮点数能够表示的数据范围一下子大了很多。正是因为这个数对应的小数点的位置是“浮动”的,它才被称为浮点数。随着指数位e的值的不同,小数点的位置也在变动。而前面BCD编码的实数,就是小数点固定在某一位的方式,称为定点数。
那么为什么用0.3 + 0.6不能得到0.9呢?因为浮点数s、e和f的计算方式导致没有办法精确表示0.3、0.6和0.9。事实上,0.1~0.9这9个数中只有0.5能够被精确地表示成二进制的浮点数,而0.3、0.6与0.9,都只是一个近似的表达。所以浮点数无论是表示还是计算其实都是近似计算。
20.浮点数可以大到3.40×10^38,也可以小到1.17×10^(−38)。但是,平时写的0.1、0.2并不是精确的数值,只是一个近似值。只有0.5这样可以表示成2^(−1)这种形式的,才是一个精确的浮点数。
举个浮点数无法精确计算小数的例子,假设有一个二进制小数0.1001,与十进制整数转换成二进制不断除以2取倒序余数的方式相反,小数点后的每一位,都表示对应的2的-N次方。那么0.1001转化成十进制就是: 1×2^(−1) + 0×2^(−2) + 0×2^(−3) + 1×2^(−4) = 0.5625。
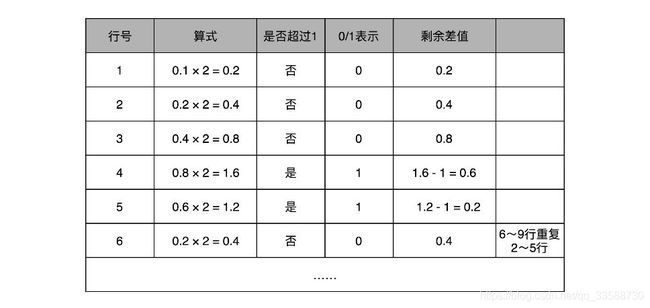
和整数的二进制表示采用“除以 2,然后看余数”的方式相比,小数部分转换成二进制是用一个相似的反方向操作,就是乘以2,然后看看是否超过1。如果超过1就记下1,并把乘以2的结果减去1,进一步循环操作。在这里就会看到,0.1其实变成了一个无限循环的二进制小数,0.000110011……..。这里的“0011”会无限循环下去,如下所示:
然后,把整数部分和小数部分拼接在一起,9.1这个十进制数就变成了1001.000110011…这样一个二进制表示。浮点数其实是用二进制的科学计数法来表示的,所以可以把小数点左移三位,这个数就变成了:
1.0010001100110011…×2^3
这个二进制的科学计数法表示就可以对应到了浮点数的格式里了。这里的符号位s = 0,对应的有效位 f=001000110011…。因为f最长只有 23 位,那这里“0011”无限循环,最多到 23 位就截止了。于是,f=00100011001100110011 001,最后的一个“0011”循环中的最后一个“1”会被截断掉。对应的指数为e,代表的应该是3(2的3次方)。因为指数位有正又有负,所以指数位在127之前代表负数,之后代表正数,那3其实对应的是加上127的偏移量130,转化成二进制就是10000010,如下所示:
然后把“s+e+f”拼在一起,就可以得到浮点数9.1的二进制表示了,变成了:010000010 0010 0011001100110011 001。如果再把这个浮点数表示换算成十进制,实际准确的值是9.09999942779541015625,并非精确的9.1。所以如果程序面对的场景是必须准确的高精度场景,不能使用float和double类型,应该使用int(数值不超过9位十进制)或者long(不超过18位十进制)以及BigDecimal(超过18位十进制)。
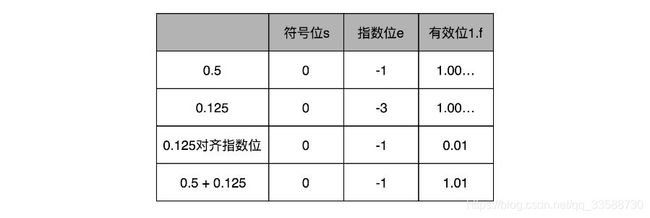
21. 浮点数的加法原理也不复杂,其实就是六个字,那就是先对齐、再计算。两个浮点数的指数位e可能是不一样的,所以要把两个指数位变成一样的,然后只去计算有效位f的加法就好了。比如0.5表示成浮点数,对应的指数位e是-1,有效位f是00…(后面全是0,f前默认有一个1)。0.125表示成浮点数对应的指数位e是-3,有效位f也还是00…(后面全是 0,f前默认有一个1)。
那么在计算0.5+0.125的浮点数运算时,首先要把两个指数位e对齐,也就是把指数位e都统一成两个其中较大的 -1,而0.125对应的有效位1.00…也要对应右移两位,因为f前面有一个默认的1,所以就会变成0.01。然后计算两者相加的有效位1.f,就变成了有效位1.01,而两者的指数位e都是-1,这样就得到了想要的加法后的结果,如下所示:
实现这样一个加法,也只需要位移,用和整数加法类似的半加器和全加器的方法就能够实现,在电路层面,也并没有引入太多新的复杂性。然而,其中指数位较小的数,需要在有效位进行右移,在右移的过程中,最右侧的有效位就被丢弃掉了。这会导致对应的指数位较小的数,在加法发生之前,就丢失精度。两个相加数的指数位差的越大,位移的位数越大,可能丢失的精度也就越大。
32位浮点数的有效位长度一共只有23位,如果两个数的指数位差出23位,较小的数右移24位之后,较小数所有的有效位就都丢失了。这也就意味着,虽然浮点数可以表示上到3.40×10^38,下到1.17×10^(−38),但在实际计算时,只要两个数差出 2^24,也就是差1600万倍左右,那这两个数相加之后,结果完全不会变化。例如下面的Java程序,让一个值为2000万的32位浮点数和1相加,会发现+1这个过程因为精度损失,被“完全抛弃”了,如下所示:
public class FloatPrecision {
public static void main(String[] args) {
float a = 20000000.0f;
float b = 1.0f;
float c = a + b;
System.out.println("c is " + c);
float d = c - a;
System.out.println("d is " + d);
}
}
对应的运行结果为:
c is 2.0E7
d is 0.0
22.在一些“积少成多”的计算过程如机器学习中,经常要通过海量样本计算出梯度或者loss,于是会出现几亿个浮点数的相加。每个浮点数可能都差不多大,但是随着累积值的越来越大,就会出现“大数吃小数”的情况。例如用一个循环相加2000万个1.0f,最终的结果会是1600万左右,而不是2000万。这是因为,加到1600万之后的加法因为精度丢失都没有了,如下所示:
public class FloatPrecision {
public static void main(String[] args) {
float sum = 0.0f;
for (int i = 0; i < 20000000; i++) {
float x = 1.0f;
sum += x;
}
System.out.println("sum is " + sum);
}
}
对应的输出结果为:
sum is 1.6777216E7为了解决这样的精度问题,科学家提出了一种叫作Kahan Summation的算法。算法的对应代码如下,可以看到同样是2000万个1.0f相加,用这种算法就得到了准确的2000万的结果:
public class KahanSummation {
public static void main(String[] args) {
float sum = 0.0f;
float c = 0.0f;
for (int i = 0; i < 20000000; i++) {
float x = 1.0f;
float y = x - c;
float t = sum + y;
c = (t-sum)-y;
sum = t;
}
System.out.println("sum is " + sum);
}
}
对应的输出结果为:
sum is 2.0E7这个算法的原理就是在每次的计算过程中,都用一次减法,把当前加法计算中损失的精度记录下来,然后在后面的循环中,把这个精度损失放在要加的小数上,再做一次运算。
根据上面的原理与例子可以看到,虽然浮点数能够表示的数据范围变大了很多,但是在实际应用的时候,由于存在精度损失,会导致加法的结果和预期不同,乃至于完全没有加上的情况。所以,一般情况下,在实践应用中,对于需要精确数值的,比如银行存款、电商交易,都会使用定点数或者整数类型。而浮点数则更适合不需要有一个非常精确的计算结果的情况。因为在真实的物理世界里,很多数值本来就不是精确的,只需要有限范围内的精度就好了。比如,从家到办公室的距离,就不存在一个100%精确的值。可以精确到公里、米,甚至厘米,但是既没有必要、也没有可能去精确到微米乃至纳米。对于浮点数加法中可能存在的精度损失,特别是大量加法运算中累积产生的巨大精度损失,可以用 Kahan Summation 这样的软件层面的算法来解决。如果是两个64位的浮点数的指数位相差52位后,较小的那个数就会因为要右移53位导致有效位数完全丢失。